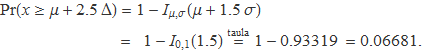Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Test khi quadrat
Test per atribuir una funció densitat de probabilitat a un experiment a partir d'un conjunt de valors
Introducció «
El valor

amb el que es comparen els valors observats i esperats d'uns resultats k, s'usa per determinar la probabilitat que el succés que ha generat els valors observats es pugui descriure amb el model amb el que s'han generat els valors esperats. Les categories apareixen de manera natural quan són discretes, com a molt s'ha de decidir alguna agrupació quan el nombre total de valors és petit i Ek pot ser zero, anul·lant el denominador. Les categories s'agrupen perquè Ek sigui almenys superior a 4. Naturalment, el subíndex k s'ha d'entendre que enumera les categories o les categories i els grups que s'han fet.
Amb una variable aleatòria continua, les categories s'han de definir com intervals de valors, assegurant de nou que Ek sigui almenys superior a 4.
Es comença aquest tema aplicant el test a un conjunt de valors per comprovar si es podrien descriure amb una funció densitat de probabilitat gaussiana. En aquesta primera aplicació se suposarà que els valors s'han generat amb un programa al qual la mitjana i variància estan donades com a paràmetres.
Després d'aquest exemple es tractarà un problema similar. També es té un conjunt de valors i es vol comprovar si es poden descriure per una funció densitat de probabilitat gaussiana; però en aquest cas se suposarà que la mitjana i la variància són desconegudes. La diferència amb el cas anterior és el nombre de graus de llibertat en el càlcul de χ2.
Conjunt de valors aleatoris vs funció gaussiana de mitjana i variància conegudes «
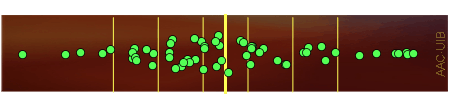
Un programa d'ordenador genera valors per a una variable aleatòria gaussiana de mitjana i desviació estàndard determinades. S'ha generat una llista de 60 valors amb el programa per a μ = 28.40 i σ = 1.95. Els valors s'han usat com abscisses del conjunt de punts mostrat a la Fig. 1.
Llista de valors »
Figura 1. Representació gràfica per mostrar els valors analitzats. Els valors són les abscisses dels punts. Les ordenades són arbitràries. La línia central groga marca la mitjana de la distribució gaussiana. La separació entre les línies grogues més primes és 3σ/5.
Es vol aplicar el test χ2 per comprovar amb quina probabilitat els valors estan distribuïts realment d'acord amb la funció de distribució de probabilitat gaussiana.
Com que la distribució gaussiana és continua, el domini de menys a més infinit s'ha de dividir en intervals. El nombre d'intervals no pots ser massa gran perquè hi ha d'haver almenys uns cinc casos dins cada un.
El domini es dividirà en 7 parts: Una part és la dels valors més petits que μ – 1.5σ, una altra és la dels valors més grans que μ +1.5σ, i les altres cinc parts són les que resulten de dividir l'interval d'amplada 3σ centrat en el valor de la mitjana dividit en 5 parts iguals. L'amplada d'aquests cinc intervals és
Δ = 3σ / 5.
A la taula adjunta es recull el nombre de valors Ok generats pel programa i el nombre esperat Ek dins cada un dels intervals.
Calcul dels valors Ek »
| Interval | |||
| 1 | 5 | 4.0 | |
| 2 | 8 | 7.0 | |
| 3 | 12 | 11.9 | |
| 4 | 12 | 14.1 | |
| 5 | 9 | 11.9 | |
| 6 | 7 | 7.0 | |
| 7 | 7 | 4.0 |
Taula 1. Nombre de valors Ok i Ek de l'exemple considerat.
Amb els valors de la Taula 1, es troba
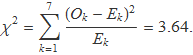
Ara cal determinar la probabilitat
Pr(χ2 ≥ 3.64)
perquè si és més petita que el 5% significarà que estam davant un cas molt improbable i, per tant, se considerarà que les dades i la funció gaussiana no són compatibles. Si és més gran que el 5%, se considerarà que són compatibles.
El valor de χ2 és la suma de 7 termes independents. Cercant a la taula de probabilitat de χ2 per a 7 graus de llibertat per a χ2/7 = 0.52 ≈ 0.5 es troba el valor 83.5. Interpolant es pot trobar més exactament
Pr(χ2 ≥ 3.64) = 82%.
Per tant, els 60 valors estan distribuïts de manera compatible amb una funció densitat de probabilitat gaussiana de mitjana 28.40 i desviació estàndard 1.95.
Conjunt de valors aleatoris vs funció gaussiana de mitjana i variància desconegudes
 «
«
Se suposarà que la llista de valors és la mateixa de 60 elements de l'apartat anterior. El que és important és que la mitjana i la variància de la funció de distribució gaussiana amb la que es volen comparar els valors es consideren desconegudes. Els seus valors, s'han de calcular a partir de la llista,
mitjana de la mostra = 28.48,
variància de la mostra = 2.34.
El domini es dividirà en set parts com abans canviant només els límits d'acord amb els valors de la mitjana i la variància de la mostra en lloc de μ i σ. Cal notar que si bé el mètode per crear els intervals és el mateix que abans, els límits dels intervals canvien (més per la variància que per la mitjana). Els nombres Ek no canviaran perquè els límits dels intervals tenen les mateixes proporcions respecte a la desviació estàndard. Però, naturalment, els valors Ok si que canviaran, perquè la posició absoluta del límits és diferent.
A la taula adjunta es recull el nombre de valors Ok generats pel programa i el nombre esperat Ek dins cada un dels intervals.
| Interval | |||
| 1 | 3 | 4.0 | |
| 2 | 8 | 7.0 | |
| 3 | 13 | 11.9 | |
| 4 | 17 | 14.1 | |
| 5 | 9 | 11.9 | |
| 6 | 4 | 7.0 | |
| 7 | 6 | 4.0 |
Taula 2. Nombre de valors Ok i Ek de l'exemple considerat. La mitjana i la variància de la gaussiana usada per calcular Ek s'han determinat a partir del conjunt de punts.
Amb els valors de la Taula 2, es troba
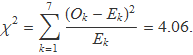
Ara cal determinar la probabilitat
Pr(χ2 ≥ 4.06)
però a diferència del cas anterior, s'ha de consultar la taula per a 5 graus de llibertat. Encara que s'hagin sumat 7 termes independents per calcular χ2, la mitjana i la variància de la gaussiana amb la que s'han calculat els valors Ek s'han determinat a partir del conjunt de punts. Per tant, s'han perdut dos graus de llibertat, ja només hi ha 5 termes independents en el sumatori.
Cercant a la taula de probabilitat de χ2 per a 5 graus de llibertat per a χ2/5 = 0.81 ≈ 0.8 es troba el valor 54.9. Interpolant es pot trobar que s'ha d'arrodonir a 54.
Pr(χ2 ≥ 3.64) = 54%.
La probabilitat està molt per damunt del límit del 5%. Per tant, els 60 valors estan distribuïts de manera compatible amb una funció densitat de probabilitat gaussiana.