
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Test khi quadrat
Nombre de gols en els partits dels Mundials de futbol i la distribució de Poisson
Introducció «
En aquest tema s'aplica el test χ2 al conjunt de dades de la Taula 1 i la funció de probabilitat de Poisson. La Taula 1 és la presentada a l'apartat sobre els gols dels mundials de futbol en la introducció a la distribució de Poisson.
| Gols | Partits | n Pμ(g) |
| 0 | 19 | 19 |
| 1 | 49 | 48 |
| 2 | 60 | 60 |
| 3 | 47 | 49 |
| 4 | 32 | 31 |
| 5 | 18 | 15 |
| ≥ 6 | 7 | 9 |
Taula 1. La primera columna és el nombre de gols g marcats en els partits durant el temps reglamentari (no s'inclouen els gols de les pròrrogues ni de les tandes de penals). La segona columna és el nombre de partits que acabaren amb aquest nombre de gols. La tercera columna és el valor de la distribució de Poisson per a Pμ(g) amb μ = 2.48, la mitjana de gols per partit. Dades extretes de Chu, S. (2003), INFORMS Transactions on Education, Vol. 3, No. 2, pàg. 62-68.
Aplicació del test χ2
 «
«
Per valorar la discrepància global entre els valors observats en una sèrie i el valor esperat, es calcularà
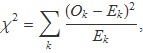
on Ok és el nombre de de partits en que es marcaren k gols i Ek és el valor esperat. Els valors de la Taula 1 donen l'histograma de la Fig. 1.
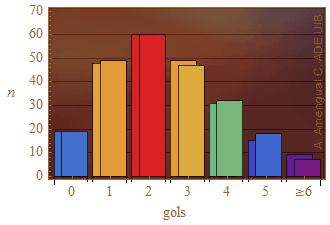
Figura 1. Histograma del nombre de gols de la Taula 1. Els valors donats per la funció de probabilitat de Poisson es mostren a les barres de darrera.
Per calcular Ek, s'ha determinat la mitjana de gols per partit, 2.48, i s'ha usat la funció de probabilitat de Poisson amb μ igual a aquesta mitjana,
![]()
Com que el nombre de gols total és n = 232, el valor esperat de partits amb k gols és
Ek = n Pμ(k)
Els partits amb 6 o més gols s'han d'agrupar. És necessari que el valor esperat sigui més gran que 4 o 5 unitats perquè s'ha de dividir per aquest valor en el càlcul de χ2. Quan no es tenen molts de casos d'algunes categories i no se'n poden aconseguir més (aquí no es poden fer més partits per tenir més casos amb sis gols) s'han d'agrupar categories (partits amb diversos resultats). El valor esperat de partits amb 6 o més gols és
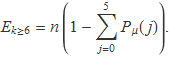
El nombre de partits amb k gols i el nombre esperat amb un decimal són
| 0 | 1 | 2 | 3 | 4 | 5 | ≥6 | |
| Ok | 19 | 49 | 60 | 47 | 32 | 18 | 7 |
| Ek | 19.4 | 48.2 | 59.7 | 49.4 | 30.6 | 15.2 | 9.4 |
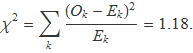
La suma s'ha fet sobre 7 valors; però la mitjana μ per calcular els valors esperats s'ha determinat usant els valors observats, per tant s'ha d'usar al taula de χ2 per a 7 – 1 = 6 graus de llibertat.
Usant la taula per a 6 graus de llibertat i χ2/6 = 0.20, es troba un probabilitat de 97.7%. Per tant,
Pr(χ2 ≥ 1.18) = 97.7%
quantifica l'acord entre Ok i Ek. Aquesta probabilitat és molt alta i es pot afirmar que la distribució de Poisson descriu el nombre de gols observats en els partits dels mundials.
Trobar que el nombre de partits amb un cert nombre de gols es pot calcular amb una funció de probabilitat és un fet que crida l'atenció inicialment. Aquí només s'ha quantificat l'acord entre els valors de la Taula 1 amb un test. Un assumpte interessant és l'anàlisi de perquè hi ha aquest bon acord. Sense entrar en detalls, la qüestió bàsica és que marcar un gol és un esdeveniment que no depèn dels gols que s'hagin marcat ni del temps que ha passat des de que es va fer el darrer gol.
