Curs ADE: GaussT1

Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.

Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.

Exercicis i problemes

Valors d'una gaussiana i probabilitat / 1r^model

1. Expressió de la gaussiana i valors «

Escriu la funció gaussiana G_1,1(x) i determina amb la calculadora el valor de la funció per a x igual a cada un dels valors indicats a la primera columna de la taula. Després comprova el resultat amb un full de càlcul amb la instrucció DISTR.NORM(x; μ; σ; 0) (el 0 final és necessari; la funció dóna el valor acumulat si es posa 1).

Solució oculta » visible

x

0.25

0.50

0.75

1.00

1.25

1.50

$x$	$G$
0.25	0.3011
0.50	0.3521
0.75	0.3867
1.00	0.3989
1.25	0.3867
1.50	0.3521

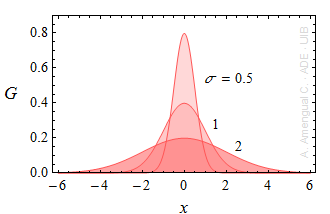
2. Comparació de tres gaussianes «

Dibuixa esquemàticament les gaussianes de mitjana 0 i variances 0.25, 1 i 4.

Solució »

3. Integral de la gaussiana canònica «

Usa la taula de la integral de la funció gaussiana per determinar la probabilitat que en un succés aleatori amb probabilitat gaussiana de mitjana 0 i variància 1 s'obtengui un valor z tal com s'indica a la primera columna.

Solució oculta » visible

Cas	Probabilitat
z < 0.58	·
z < 0.79	·
z < -0.37	·
z < -0.32	·
z > 0.58	·
z > -0.37	·
-0.32 < z < 0.58	·

4. Integral d'una gaussiana «

Usa la taula de la integral de la funció gaussiana per determinar la probabilitat que en un succés aleatori amb probabilitat gaussiana de mitjana 6.14 i desviació estàndard 4.66 s'obtengui un valor z tal com s'indica a la primera columna.

Solució oculta » visible

Cas	Probabilitat
z < 8.56	·
z < 5.53	·
z > 8.56	·
5.53 < z < 8.56	·

5. Càlcul de valors per interpolació «

Solució »

6. Error en el càlcul d'interpolació «

Usa taula de la integral de la funció gaussiana per determinar la probabilitat que en un succés aleatori amb probabilitat gaussiana de mitjana 0 i variància 1 s'obtengui un valor més petit que 0.3650. Com que aquest valor no apareix a la taula, s'ha de fer una interpolació. Per determinar la incertesa sobre la probabilitat calculada suposa que la única incertesa és la dels valors de la taula i val ±0.000005.

Solució »

7. Càlcul de probabilitats «

Calcula la probabilitat que en un succés aleatori amb probabilitat gaussiana de mitjana 3.86 i desviació estàndard 6.25 s'obtengui un valor x∈[5.6538,5.6706].

Solució »

8. Càlcul de probabilitats «

Usa el següent fragment de la taula de la integral de la funció gaussiana

a\|b	0.	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
0.3	0.61791	0.62172	0.62552	0.62930	0.63307	0.63683	0.64058	0.64431	0.64803	0.65173
0.4	0.65542	0.65910	0.66276	0.66640	0.67003	0.67364	0.67724	0.68082	0.68439	0.68793
0.5	0.69146	0.69497	0.69847	0.70194	0.70540	0.70884	0.71226	0.71566	0.71904	0.72240

per determinar la probabilitat que en un succés aleatori amb probabilitat gaussiana de mitjana 2.85 i desviació estàndard 6.06 s'obtengui un valor z₀ tal com s'indica a la primera columna. Dóna la probabilitat en tant per cent i amb un decimal.

Solució oculta » visible

Cas

z_{0} < 4.8498

z_{0} < 5.4558

z_{0} > 4.8498

4.8498 < z_{0} < 5.4558

Cas	Equivalent	Probabiliat (%)
$z_{0} < 4.8498$	$x_{0} < 0.330$	62.93
$z_{0} < 5.4558$	$x_{0} < 0.430$	66.64
$z_{0} > 4.8498$	$x_{0} > 0.330$	37.07
$4.8498 < z_{0} < 5.4558$	$0.330 < x_{0} < 0.430$	3.71

Per trobar les dues primeres probabilitats, s'ha de fer el canvi x₀ = (z₀ – μ)/σ. Els valors x₀ es poden consultar a la taula. La tercera probabilitat és la complementària de la primera. La quarta probabilitat és la resta de les probabilitats 2 menys 1.

9. Problema invers «

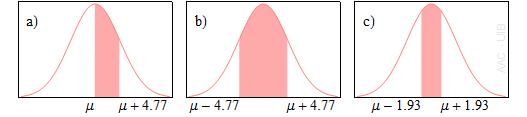
Una variable aleatòria gaussiana té mitjana μ = 9 i desviació estàndard σ = 5. Què ha de valer a perquè la probabilitat que el valor de la variable estigui dins l'interval:

a) [9, 9 + a] valgui 0.33?

b) [9 – a, 9 + a] valgui 0.66?

c) [9 – a, 9 + a] valgui 0.30?

Fes tres esquemes de la gaussiana amb les àrees que representen les probabilitats donades.

Solució »

10. Probabilitats que s'han de saber «

A partir de 9 mesures has determinat que la mitjana i la desviació estàndard de l’energia d’un tipus de partícules idèntiques és E = 7.07 ± 0.15 J. Contesta les preguntes següents justificant les respostes:

a) Què val l’error estàndard?

b) Quina és la probabilitat que es faci una altra mesura i s’obtengui un valor dins l’interval [6.92, 7.22]?

c) És possible que amb el mateix dispositiu experimental es faci una mesura més i s’obtengui que l’energia és més gran que 7.22? Si la teva resposta és no, explica el motiu. Si és si, calcula quina és la probabilitat que això passi.

Solució »

11. Límit de la distribució binomial «

Trobam escrit en un llibre que “el valor de B_n,p(468) per a n = 1112 i p = 0.39 és 0.00457”. Segurament la teva calculadora no te permetrà comprovar-ho aplicant la definició de la funció de distribució binomial.
a) Quin càlcul pots fer amb la calculadora per comprovar si és o no possible aquest valor?
b) És el valor possible?

Solució »

12. Límit de la distribució binomial «

La probabilitat d'èxit d'un succés és 0.20 i la probabilitat de que almenys 364 successos de 1839 siguin d'èxit és 0.59685. Atès que la calculadora no te permet comprovar-ho aplicant la distribució binomial, com pots fer un càlcul aproximat per comprovar-ho? Què dóna el càlcul?

Solució »

13. Probabiitat que una mesura sigui dolenta «

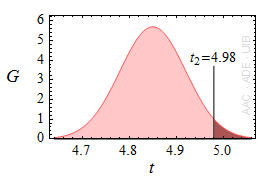
Es mesura un interval de temps amb error aleatori. El resultat és t_m = 4.85 ± 0.07 s. Considera que 0.07 és la desviació estàndard. Quina és la probabilitat que el temps mesurat realment valgui més que t₂ = 4.98 s?

Solució »

14. Probabiitat que una mesura sigui dolenta «

El conjunt de valors de taula següent corresponen als resultats de mesures d'una variable x amb presència d'errors aleatoris. Calcula la mitjana, l'error estàndard i la probabilitat que una mesura de la variable doni un valor a una distància de la mitjana igual o superior a la que està la dada més llunyana de la taula. Llavors, aplica el criteri de Chauvenet a aquesta dada.

8.29

8.32

8.17

8.45

8.27

7.78

8.32

8.12

Solució »

15. Probabiitat que una mesura sigui dolenta «

Repeteix l'exercici anterior amb aquest altre conjunt de valors.

7.030

6.964

7.028

6.942

7.037

6.938

6.943

7.042

Solució »