Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Exercicis i problemes
Teoria de la probabilitat / 2nmodel
1. Funció densitat de probabilitat trapezoidal
 «
«
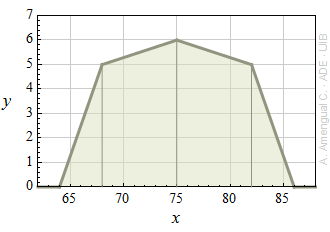
La representació gràfica d'una funció de distribució de probabilitat sense normalitzar d'una variable aleatòria X continua es mostra a la figura adjunta. La funció val zero fora del domini mostrat. Quina és la probabilitat que
a) x > 82.0?
b) 64.0 > x > 82.0?
c) x < 83.9?
d) x > 83.9?
Solució »
2. Funció densitat de probabilitat amb punta
 «
«
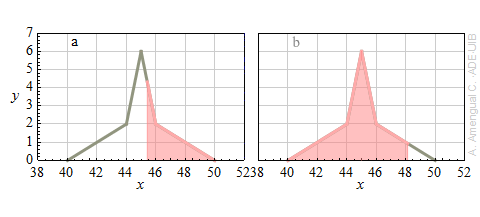
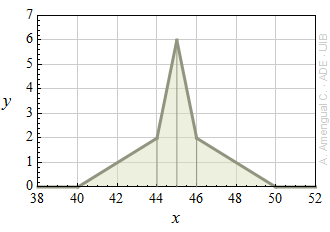
La representació gràfica d'una funció de distribució de probabilitat sense normalitzar d'una variable aleatòria X continua es mostra a la figura adjunta. La funció val zero fora del domini mostrat. Quina és la probabilitat que
a) x > 45.4?
b) 45.0 > x > 45.4?
c) x < 48.1?
d) x > 48.1?
Solució »
3. Demostració
 «
«
Una variable aleatòria positiva X té la densitat de probabilitat sense normalitzar mostrada a la figura adjunta (la densitat es manté igual a zero per a x > 1.0).
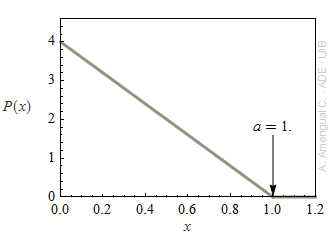
a) Justifica de manera senzilla que P(x) s'ha de multiplicar per α = 0.500 per tenir una densitat de probabilitat normalitzada.
b) Calcula el valor esperat de la variable aleatòria X.
Solució »
4. Desviació estàndard funció densitat de probabilitat parell
 «
«
a) Calcula la constant A per la qual s'ha de dividir la funció P(x) de la figura perquè la seva integral sobre tot el domini valgui 1.
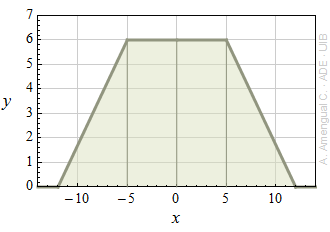
b) Si la funció P(x) dividida per A és la funció densitat de probabilitat d'una variable aleatòria X, el valor esperat de X és zero i l'expressió que dòna la variància és
![]()
Demostra que el resultat d'aquesta integral és igual a
![]()
c) Usa el resultat de l'apartat b per calcular la variància. Què val la desviació estàndard?
Solució »