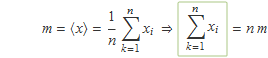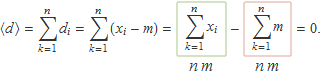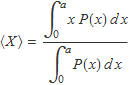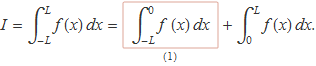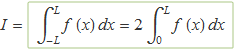Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Exercicis i problemes
Teoria de la probabilitat / 1r model
1. Demostració  «
«
La mitjana m de n nombres xi és la suma dels nombres dividida per n. La desviació de cada nombre respecte a la mitjana és di = xi – m. a) Fes la comprovació que la mitjana dels nombres di és zero amb el conjunt de valors {22, 6, 8}. b) Fes la demostració general que la mitjana dels nombres di és zero.
Solució »
2. Funció densitat de probabilitat dent de serra  «
«
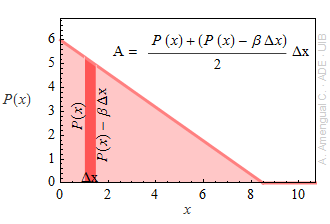
Una variable aleatòria positiva X té la densitat de probabilitat sense normalitzar mostrada a la figura adjunta (la densitat es manté igual a zero per a x > 4.0).
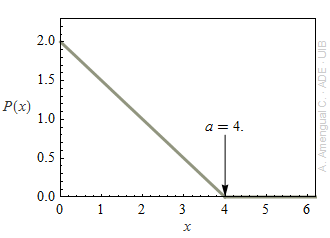
a) Justifica de manera senzilla que P(x) s'ha de multiplicar per α = 0.250 per tenir una densitat de probabilitat normalitzada.
b) Calcula el valor esperat de la variable aleatòria X.
Solució »
3. Centre de masses i mitjana  «
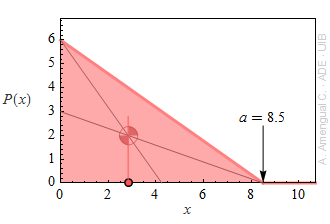
«
L'expressió que dóna el valor esperat d'una variable aleatòria X amb una funció de distribució de probabilitat P(x) és matemàticament igual a l'expressió que dóna l'abscisssa del centre de masses d'una làmina homogènea de massa M amb la forma de la funció P(x)
![]()
a) Comprova que la integral que dóna xcm és equivalent a la del valor esperat de X.
b) El centre de masses d'un triangle està a la intersecció de les rectes mitjanes (una mitjana passa pel centre d'un costat i pel vèrtex oposat). Cerca gràficament la posició del centre de masses, calcula el valor esperat de X per a la funció de la figura i comprova que és igual a l'abscissa del centre de masses.
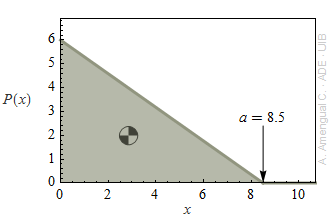
Solució »
4. Funció densitat de probabilitat trapezoidal  «
«
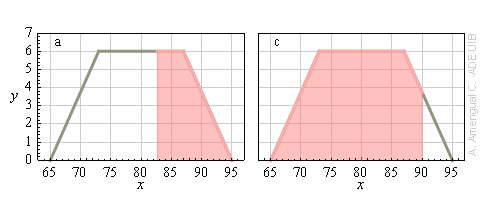
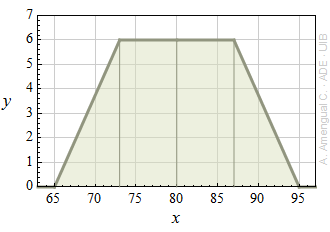
La representació gràfica d'una funció de distribució de probabilitat sense normalitzar d'una variable aleatòria X continua es mostra a la figura adjunta. La funció val zero fora del domini mostrat. Quina és la probabilitat que
a) x > 82.7?
b) 80.0 < x < 82.7?
c) x < 90.0?
d) x > 90.0?
Solució »
5. Funció densitat de probabilitat amb punta  «
«
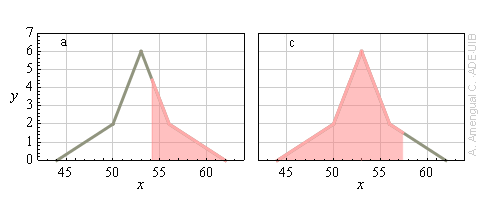
La representació gràfica d'una funció de distribució de probabilitat sense normalitzar d'una variable aleatòria X continua es mostra a la figura adjunta. La funció val zero fora del domini mostrat. Quina és la probabilitat que
a) x > 54.2?
b) 53.0 < x < 54.2?
c) x < 57.4?
d) x > 57.4?

Solució »
6. Funció densitat de probabilitat exponencial  «
«
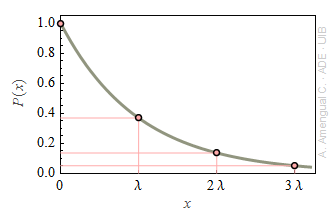
Considera la funció densitat de probabilitat per a la variable aleatòria X,
![]()
a) Calcula el valor de la constant A perquè P(x) estigui normalitzada.
b) Fes un gràfic esquemàtic de la funció P(x).
c) Calcula el valor esperat de X.
d) Calcula la desviació estàndard σ.
e) Què val la probabilitat que el valor de X estigui dins l'interval d'amplada 2σ centrat en el valor esperat?
Solució »
7. Funció triangular  «
«
a) Calcula la constant A per la qual s'ha de dividir la funció P(x) de la figura perquè la seva integral sobre tot el domini valgui 1.
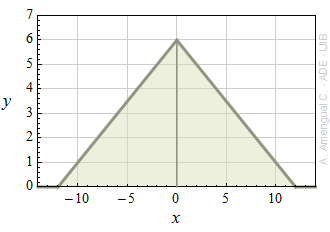
b) Si la funció P(x) dividida per A és la funció densitat de probabilitat d'una variable aleatòria X, el valor esperat de X és zero i l'expressió que dòna la variància és
![]()
Demostra que el resultat d'aquesta integral és igual a
![]()
c) Usa el resultat de l'apartat b per calcular la variància. Què val la desviació estàndard?
Solució »
8. Funció cosinus  «
«
Considera la funció
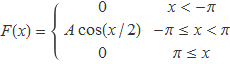
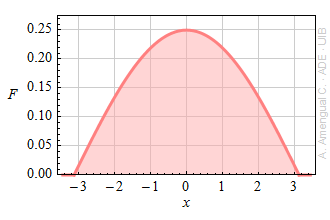
a) Què ha de valer la constant A perquè F pugui ser la funció densitat de probabilitat normalitzada d'una variable aleatòria X.
b) Dibuixa la funció F(x).
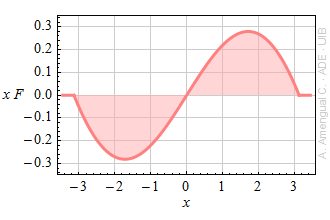
c) Quina integració s'ha de fer per calcular el valor esperat de X? Què val el valor esperat?
d) Calcula la variància de la funció donada.
Solució »