Figura 1. Valors experimentals representats per les abscisses d'uns punts.

Si la mitjana i la desviació estàndard de la mostra d'una variable x mesurada diverses vegades donen 55 i 5, respectivament, hi ha una probabilitat del 32 % que una nova mesura de x estigui fora de l'interval (50, 60). Aquest interval correspon a D₁ = (μ – σ, μ + σ), la probabilitat que |x – μ| < σ és del 68 % i la nova mesura quedarà fora de l'interval amb la probabilitat complementària.

La probabilitat que la nova mesura quedi fora de l'interval més ampla D₂ = (μ – 2σ, μ + 2σ) segueix essent notable, perquè encara és del 4.5 %. Que una mesura addicional quedi fora de l'interval D₁ no es considera estrany, que quedi fora de l'interval D₂ no passarà tant sovint, però tampoc es considerarà un succés estrany. Com més mesures amb el mateix error aleatori es fan, la probabilitat que alguna quedi fora dels intervals esmentats creix.

Donat un conjunt de mesures, amb una d'elles bastant enfora de la mitjana de les altres, es planteja la qüestió de si és probable que hi estigui o si convé pensar en la presència d'algun factor que justifiqui un anàlisi més detallat de la situació (per exemple, que un canvi de temperatura ha provocat un efecte que no es preveia) o, en un cas extrem, en la presència d'una errada important que justifiqui rebutjar la mesura.

Les barres d'un histograma donen el nombre de valors dins intervals determinats. Amb la divisió de totes les alçades de les barres pel nombre total de valors, l'altura d'una barra serà proporcional a la freqüència amb que la variable ha pres valors dins el seu interval. S'espera que les freqüències s'aproximin als valors d'una distribució continua si el nombre de mesures és suficientment gran. Usant aquesta distribució continua per a la qual es coneixen les propietats, els nombres de valors dins cada un dels intervals de l'histograma es poden calcular de manera aproximada multiplicant l'àrea sota la distribució continua pel nombre de valors total. Com que l'àrea sota una gaussiana fora de l'interval D₂ = (μ – 2σ, μ + 2σ) és 0.045, un histograma construït amb n punts tendrà 0.045n punts fora de l'interval D₂. Si n és inferior a 20, 0.045n és inferior a 1 i no cal esperar que cap valor quedi fora de l'interval. Aquesta idea és la que s'usa a continuació per analitzar una dada que es troba lluny de la mitjana de les altres.

La taula següent mostra 10 valors d'una variable mesurada amb errors aleatoris i unitats arbitràries.

El valor

x_r = 0.587

s'ha marcat amb color vermell perquè és bastant més gran que els altres. Els valors de la taula s'han usat com abscisses per dibuixar els punts de la Fig. 2 i es veu clar que x_r queda enfora de l'agrupació dels altres.

La mitjana dels 10 punts és

mentre que la mitjana sense incloure el valor llunyà x_r és

Encara que les dues mitjanes serien iguals si s'arrodoneixen a dos decimals, l'existència d'un punt tant llunyà s'ha d'analitzar.

Figura 2. Representació dels valors de la taula. La marca de color verd indica la mitjana dels punts verds; l'altra, la mitjana amb el punt vermell inclòs.

Pot ser que algun tipus d'error en la mesura hagi donat el valor més gran? O és 0.587 un valor tan vàlid com els altres?

Considerem que es fessin 5000 mesures en lloc de només 9. A la Fig. 3 es mostra un histograma de cinc mil mesures. Sobre l'eix d'abscisses s'han posat els punts de la Fig. 2. El punt vermell està dins la base d'una columna d'una altura de quasi 40 unitats. Si es fessin 5000 mesures, no seria estrany que en sortissin algunes amb un valor al voltant de 0.587. De fet, vist l'histograma, el que seria estrany és que no en sortís cap.

El nombre de mesures que donen un valor x ≥ x_r = 0.587 es pot determinar sumant els valors de la columna sobre el punt vermell i els de les columnes que queden a la seva dreta.

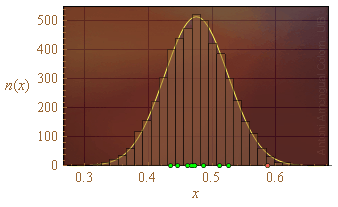
Figura 3. Histograma de 5000 punts amb els valors de la Fig. 2 sobre l'eix d'abscisses. La línia groga és la gaussiana centrada en la mitjana de x multiplicada per 5000.

Sense haver de recórrer a l'histograma d'un conjunt particular de n punts, el nombre de mesures que donen un valor x ≥ x_r es pot calcular aproximadament multiplicant n per l'àrea de la gaussiana per a  x ≥ x_r (Fig. 4)

Per a n = 5000 i x_r = 0.587, la integral multiplicada per n dóna 62.7. S'esperaran unes 62 mesures per damunt de 0.587 si se'n fan cinc mil. Però, per a n = 10, la integral multiplicada per n dóna només 0.13, un valor molt lluny de la unitat. Si només s'han fet 10 mesures i s'ha obtingut un valor com 0.587, s'ha de pensar que s'ha donat un cas molt poc probable o que ha passat alguna cosa perquè s'obtingués un valor tan alt i convé revisar l'experiment. Es prefereix pensar en la segona opció: Hi ha d'haver alguna cosa per la qual s'ha obtingut un valor llunyà quan no se n'esperava ni tans sols un.

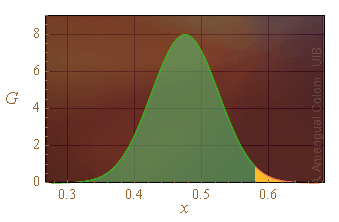
Figura 4. L'àrea de la zona taronja dóna la probabilitat d'obtenir x per damunt de x_r = 0.587. Si es fan n mesures, el valor de l'àrea multiplicat per n dóna el nombre de mesures que cal esperar surtin superiors a x_r.

S'estableix un límit per considerar que una mesura s'ha d'analitzar amb més detall per trobar-se massa enfora de la mitjana. El criteri de Chauvenet^‡ estableix que si

convé analitzar les circumstàncies que han donat el valor llunyà. Cal remarcar que el límit 0.5 es pot interpretar com que una de cada dues vegades que es repetís la sèrie de n mesures s'obtendria un valor superior a x_r.

El següent és un cas semblant per considerar. La suma dels punts de 10 daus està entre 10 i 60. Si els 10 daus es llancen només cinc vegades, resultarà molt estrany que la suma dels punts sigui en algun cas un dels valors extrems. El valor és possible, però la probabilitat és tan baixa que, si es dóna, val més pensar que els daus estan trucats per afavorir el valor extrem i no que s'hagi donat netament un cas tan improbable. Convendria fer més llançaments per tenir més informació, però si no fos possible, s'ha de prendre una decisió amb la informació disponible. Això és el que pot succeir amb valors experimentals quan no resulta fàcil fer més mesures.