Es tracta de trobar una recta d'ajust a un conjunt de n punts {x_i, y_i} quan la incertesa sobre les ordenades no és constant.

Suposem que entre les dues variables x i y existeix la relació

y = f(x) = a₁ x + a₀.

amb unes constant a₁ i a₀ desconegudes. Per a diversos valors x = x_i es pot fer una mesura per determinar el valor de la variable y. El valor mesurat tendrà sempre una incertesa. Se suposarà que la mesura de la variable y per a x = x_i és un mostreig d'una distribució gaussiana de mitjana f(x_i) i variança σ_y² = σ_i². La variança depèn de l'abscissa.

La probabilitat que es mesuri y = y_i ± σ_i per a x = x_i és proporcional a

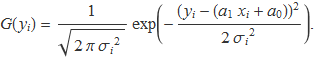
Si es fan n mesures per a un conjunt de valors {x₁, x₂, ..., x_n}, la probabilitat d'obtenir un conjunt de valors {y₁, y₂, ..., y_n} serà proporcional al producte de les probabilitats. Com que el producte d'exponencials és igual a l'exponencial de la suma dels exponents, la probabilitat serà proporcional a

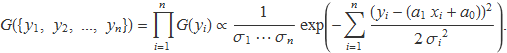
Ara es tracta de trobar els paràmetres a₁ i a₀ i farà de manera semblant a com es va fer quan EnllaSTema[les variances σ_i tenien totes el mateix valor wt_MinimsQuadrats035_GaussR011.nb].

La probabilitat G({y₁, y₂, ..., y_n}) no es pot avaluar numèricament perquè a₁, a₀ no tenen valors coneguts, però s'establirà el següent:

Els valors de a₁ i a₀ que s'usaran per definir la relació lineal entre les variables y i x seran els valors que facin més probable haver obtingut la sèrie de valors {y₁, ..., y_n}.

Per tant, cal cercar el màxim de G resolent les equacions

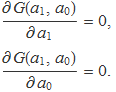
Definint els pesos

w_i = σ_i^-2

i usant les expressions de G i de la derivada d'una exponencial, les dues condicions anteriors es converteixen en

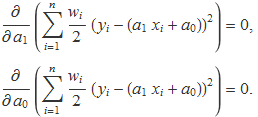
Fent la derivada es troba

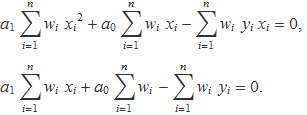
Aquestes són dues equacions que es poden escriure en forma matricial:

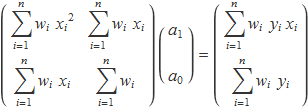
La solució usant la regla de Cramer és

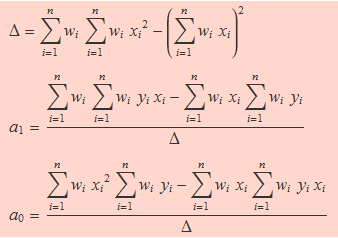
Aquestes solucions es poden escriure de manera compacta usant alguna de les notacions presentades quan la incertesa sobre els valors de les ordenades eren els mateixos.