L'ERROR PROBABLE D'UNA MITJANA

per Student

INTRODUCCIÓ

Qualsevol experiment es pot considerar un element d'una «població» d'experiments que es poden realitzar en les mateixes condicions. Una sèrie d'experiments és una mostra extreta d'aquesta població.

Ara, qualsevol sèrie d'experiments només té valor en la mesura que ens permet formar un judici sobre les constants estadístiques de la població a la qual pertanyen els experiments. En la majoria de casos, la qüestió finalment versa sobre el valor d'una mitjana, ja sigui directament o com la diferència mitjana entre dues quantitats.

Si el nombre d'experiments és molt gran, podem tenir informació precisa sobre el valor de la mitjana, però si la mostra és petita, tenim dues fonts d'incertesa: (1) a causa de «l'error de mostreig aleatori» la mitjana de la nostra sèrie d'experiments es desvia més o menys àmpliament de la mitjana de la població, i (2) la mostra no és prou gran per determinar quina és la llei de distribució dels elements. És usual, però, suposar una distribució normal, pel fet que, en un nombre molt nombrós de casos, l'aproximació és tan gran que una mostra petita no dóna cap informació real de la manera com la població es desvia de la normalitat: atès que s'ha d'assumir una llei de distribució, és millor treballar amb una corba les ordenades i l'àrea de la qual es tenen tabulades, i amb propietats ben conegudes. Aquest supòsit és el que s'assumeix en el present document, de manera que les conclusions no són aplicables estrictament a poblacions que se sap que no es distribueixen normalment, si bé sembla probable que la desviació de la normalitat ha de ser molt extrema per conduir a un error greu. Ens referim aquí únicament a la primera de les dues fonts d'incertesa esmentades.

El mètode usual de determinar la probabilitat que la mitjana de la població es trobi dins una distància donada de la mitjana de la mostra és assumir un distribució normal al voltant de la mitjana de la mostra amb una desviació estàndard igual a s/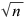, on s és la desviació estàndard de la mostra, i utilitzar llavors les taules de la integral de probabilitat.

Però, a mesura que es disminueix el nombre d'experiments, el valor de la desviació estàndard trobat a partir de la mostra d'experiments esdevé ell mateix subjecte a un error creixent, fins que els judicis assolits d'aquesta manera es poden convertir en totalment enganyosos.

En el treball de rutina, hi ha dues maneres de fer front a aquesta dificultat: (1) un experiment es pot repetir moltes vegades, fins que s'obté una sèrie tan llarga que la desviació estàndard es determina d'una vegada per totes amb la suficient precisió. Aquest valor se pot utilitzar llavors per a una sèrie posterior més curta d'experiments similars. (2) Quan els experiments es realitzen per duplicat en el curs natural de la feina, la mitjana quadràtica de la diferència entre els corresponents parells és igual a la desviació estàndard de la població multiplicat per . Podem així combinar diverses sèries d'experiments amb el propòsit de determinar la desviació estàndard. Però a causa del canvi secular, el valor obtingut és gairebé sempre massa baix, els experiments successius tenen correlació positiva.

Hi ha altres experiments que no es poden repetir molt sovint de manera fàcil. En aquests casos, de vegades és necessari jutjar la certesa dels resultats a partir d'una mostra molt petita, la qual proporciona a més l'única indicació de la variabilitat. Alguns experiments químics, molts de biològiques, la majoria dels agrícoles i els experiments de gran escala pertanyen a aquesta classe, que fins ara ha estat gairebé fora de l'abast de la investigació estadística.

Un cop més, tot i que és ben conegut que el mètode d'utilització de la corba normal només és fiable quan la mostra és «gran», ningú ens ha dit encara clarament on s'ha de traçar el límit entre mostres «grans» i «petites».

L'objectiu d'aquest treball és determinar el punt en el qual podem fer servir les taules de la integral de probabilitat per jutjar la significació de la mitjana d'una sèrie d'experiments, i proporcionar taules alternatives per usar quan el nombre d'experiments sigui massa petit.

THE PROBABLE ERROR OF A MEAN

by Student

INTRODUCTION

Any experiment may he regarded as forming an individual of a “population” of experiments which might he performed under the same conditions. A series of experiments is a sample drawn from this population.

Now any series of experiments is only of value in so far as it enables us to form a judgment as to the statistical constants of the population to which the experiments belong. In a greater number of cases the question finally turns on the value of a mean, either directly, or as the mean difference between the two quantities.

If the number of experiments be very large, we may have precise information as to the value of the mean, but if our sample be small, we have two sources of uncertainty: (1) owing to the “error of random sampling” the mean of our series of experiments deviates more or less widely from the mean of the population, and (2) the sample is not sufficiently large to determine what is the law of distribution of individuals. It is usual, however, to assume a normal distribution, because, in a very large number of cases, this gives an approximation so close that a small sample will give no real information as to the manner in which the population deviates from normality: since some law of distribution must he assumed it is better to work with a curve whose area and ordinates are tabled, and whose properties are well known. This assumption is accordingly made in the present paper, so that its conclusions are not strictly applicable to populations known not to be normally distributed; yet it appears probable that the deviation from normality must be very extreme to load to serious error. We are concerned here solely with the first of these two sources of uncertainty.

The usual method of determining the probability that the mean of the population lies within a given distance of the mean of the sample is to assume a normal distribution about the mean of the sample with a standard deviation equal to s/, where s is the standard deviation of the sample, and to use the tables of the probability integral.

But, as we decrease the number of experiments, the value of the standard deviation found from the sample of experiments becomes itself subject to an increasing error, until judgments reached in this way may become altogether misleading.

In routine work there are two ways of dealing with this difficulty: (1) an experiment may he repeated many times, until such a long series is obtained that the standard deviation is determined once and for all with sufficient accuracy. This value can then he used for subsequent shorter series of similar experiments. (2) Where experiments are done in duplicate in the natural course of the work, the mean square of the difference between corresponding pairs is equal to the standard deviation of the population multiplied by . We can thus combine together several series of experiments for the purpose of determining the standard deviation. Owing however to secular change, the value obtained is nearly always too low, successive experiments being positively correlated.

There are other experiments, however, which cannot easily be repeated very often; in such cases it is sometimes necessary to judge of the certainty of the results from a very small sample, which itself affords the only indication of the variability. Some chemical, many biological, and most agricultural and large scale experiments belong to this class, which has hitherto been almost outside the range of statistical inquiry.

Again, although it is well known that the method of using the normal curve is only trustworthy when the sample is “large”, no one has yet told us very clearly where the limit between “large” and “small” samples is to be drawn.

The aim of the present paper is to determine the point at which we may use the tables of the probability integral in judging of the significance of the mean of a series of experiments, and to furnish alternative tables for use when the number of experiments is too few.