
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Ajusts per mínims quadrats
Ajust amb una recta que passa per l'origen
Introducció «
A la Fig. 1 es mostra una línia que passa per l'origen, sis punts i els segments verticals que marquen la distància entre les ordenades dels punts i la línia. Els números al costat dels punts són les distàncies amb les mateixes unitats de l'eix d'ordenades. A la part superior del gràfic es dóna la suma dels quadrats de les distàncies. Amb els dos botons que hi ha a baix de la figura, es pot canviar el pendent de la recta. Si el pendent s'augmenta des del valor inicial mostrat, les distàncies canvien i la suma dels quadrats passa per un valor mínim.
Figura 1. Sis punts donats (les coordenades s'indiquen a la Taula 1) i les distàncies a una recta que passa per l'origen (usa els botons per augmentar o disminuir el pendent de la recta).
La separació entre cada punt i la recta s'està mesurant en direcció vertical. Aquesta separació no és la distància del punt a la recta que, per definició, es mesura en la direcció perpendicular a la recta. Aquí interessa la diferència entre l'ordenada d'un punt i l'ordenada de la recta per a la mateixa abscissa i, per tant, la separació es mesura verticalment.
Determinació del pendent de la recta que ajusta els punts
 «
«
Es considerarà el problema general de la determinació del pendent de la recta
f(x) = a1 x
perquè la suma dels quadrats de les separacions entre la recta i un conjunt donat de n punts (xi, yi), i = 1..n, sigui mínima. La suma s'escriurà S(a1) per indicar que només depèn del pendent (els punts tenen coordenades amb valors determinats). La suma val
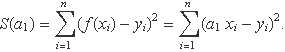
El gràfic de S(a1) entre 1 i 1.5 per al conjunt de punts de la Fig. 1, es mostra a la figura següent. La corba és mínima per a un valor pròxim a a1 = 1.24.
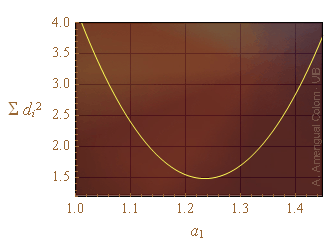
Figura 2. La suma dels quadrats de les distàncies dels sis punts de l'exemple de la Fig. 1 en funció del paràmetre a1 que dóna el pendent de la recta. La suma té un valor mínim per a un valor del pendent proper a 1.24.
El valor de a1 on S és exactament mínima es pot obtenir cercant la solució de
![]()
Estàs avesat a derivar respecte de x? Els mínims i màxims d'una funció f(x) se cerquen amb l'equació que resulta d'igualar a zero la derivada de la funció respecte de x. Per a una funció que depengui d'una altra variable, els extrems s'han de cercar derivant la funció respecte d'aquesta altra variable i això és el que s'acaba de fer.
Resolució de l'equació que dóna el pendent
 «
«
La derivada d'una suma de funcions és la suma de les derivades, per tant
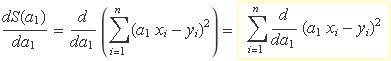
La derivada de (a1 xi – yi)2 respecte de a1 és 2 (a1 xi – yi) xi, llavors
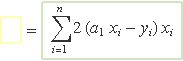
Usant les propietats dels sumatoris
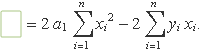
Finalment, s'iguala la derivada a 0 i s'obté l'equació
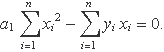
D'aquí s'obté directament
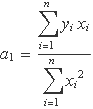
Exemple
 «
«
Per al conjunt de sis punts de l'exemple mostrat a la Fig. 1 es té
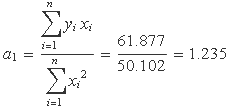
A la taula següent es donen les coordenades dels punts, les sumes per determinar a1 i el càlcul de S mínim.
| xi | yi | xi yi | xi2 | a1 xi | di = a1 xi - yi | di2 |
| 0.7736 | 0.2336 | 0.1807 | 0.5984 | 0.9554 | 0.7218 | 0.5210 |
| 1.5081 | 2.2498 | 3.3930 | 2.2744 | 1.8625 | -0.3873 | 0.1500 |
| 2.2141 | 2.1532 | 4.7673 | 4.9023 | 2.7345 | 0.5813 | 0.3379 |
| 2.9480 | 3.6667 | 10.8094 | 8.6905 | 3.6408 | -0.0259 | 0.0007 |
| 3.6486 | 5.1484 | 18.7846 | 13.3123 | 4.5061 | -0.6423 | 0.4126 |
| 4.5082 | 5.3108 | 23.9423 | 20.3242 | 5.5678 | 0.2570 | 0.0661 |
| Σ = 61.877 | Σ = 50.102 | Σ = 1.4883 |
Taula 1. Taula amb les coordenades dels punts de l'exemple de la Fig. 1 i les càlculs per obtenir el pendent de la recta que s'ajusta als punts.
