Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Exercicis i problemes
Distribució de Poisson / 3r model
1. Valors de la funció de probabilitat
 «
«
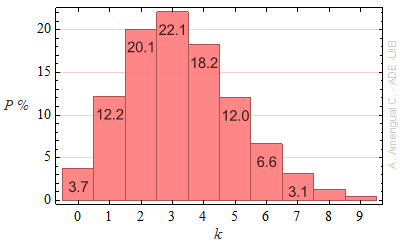
Calcula els valors de la funció densitat de Poisson Pμ(k) per a μ = 3.3 i k = 0, 1, ..., 9. Fes un histograma de barres amb els valors calculats.
Solució »
2. Nombre de desintegracions
 «
«
Una mostra radioactiva conté 4.7 1020 àtoms, cadascun dels quals té una probabilitat p = 5.6 10-21 de desintegrar-se en un determinat interval de 6 segons. a) Quin és el nombre mitjà esperat μ de desintegracions de la mostra en 6 s? b) Calcula la probabilitat d'observar k desintegracions en un interval de 6 s, per a k = 0, 1, 2, 3. c) Quina és la probabilitat d'observar 4 o més desintegracions en un interval de 6 s?
Solució »
3. Mostra radioactiva
 «
«
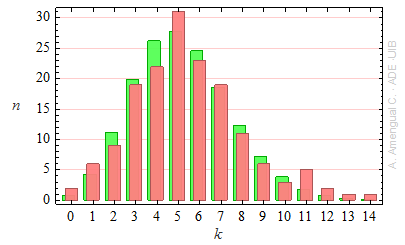
Una mostra radioactiva dóna una mitjana de 5.3 desintegracions per minut. Una parella d'estudiants compta 160 vegades el nombre de desintegracions durant un minut i suma el nombre n de vegades que ha obtingut un determinat nombre k de desintegracions en un minut. La taula del resultat és la següent.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| 2 | 6 | 9 | 19 | 22 | 31 | 23 | 19 | 11 | 6 | 3 | 5 | 2 | 1 | 1 |
Fer un histograma dels resultats junt amb l'histograma de la distribució esperada.
Solució »
4. Comparació variància de la mostra i de la població
 «
«
Per fer un experiment en el laboratori de Física Nuclear, es mesuren les desintegracions d'una mostra radioactiva amb un comptador Geiger. De manera automàtica es fan repetides mesures del nombre de desintegracions durant un temps τ. El nombre n de vegades que s'ha obtingut un determinat nombre k de desintegracions en el temps τ es recull en la taula següent
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| 12 | 52 | 86 | 145 | 170 | 151 | 113 | 74 | 29 | 18 | 14 | 3 | 1 | 2 |
a) Calcula el nombre mitjà de desintegracions en el temps τ a partir de la informació d'aquesta taula.
b) Calcula la variància del nombre de desintegracions en el temps τ.
c) Compara els resultats dels dos apartats anteriors.
Solució »
5. Aplicació
 «
«
El 2.0 % d'esferes per a bolígrafs que surten d'una línia de producció tenen un diàmetre més petit que el necessari. Calcula la probabilitat de trobar 3 esferes per a bolígrafs d'un diàmetre més petit que el necessari d'un conjunt elegit a l'atzar de
a) 100 elements.
b) 140 elements.
Solució »
6. Cobrament de factures
 «
«
Una empresa emet factures diàriament amb una data de venciment a un mes. Els clients tenen des del dia que s'emet la factura fins a un mes després per pagar-les. L'empresa veu que hi ha una mitjana de 7 factures que no s'han pagat el dia del venciment. Calcula la probabilitat que el nombre de factures vençudes sense pagar sigui
a) 3 un dia determinat.
b) 12 entre un dia i l'endemà.
Solució »
7. Control de qualitat
 «
«
En el control de qualitat de la producció a gran escala d'una fàbrica es troben en mitjana 38 components per minut que s’han de rebutjar. Calcula la probabilitat que s’hagin de rebutjar
a) 222 components en 6 minuts;
b) almenys 562 components en 15 minuts;
c) més de 198 components en 5 minuts.
Solució »
8. Límit de la funció de probabilitat binomial
 «
«
Segurament no podràs comprovar amb la calculadora que el valor de Bn,p(25) per a n = 1186 i p = 0.014 és 0.01245 aplicant la definició de la funció de distribució binomial, però la distribució de Poisson serveix per calcular si és un valor més o menys real. Què dóna el valor aproximat amb la distribució de Poisson?
Solució »