Es puja a una torre i es llança una pilota des d'una altura de 17.9 m amb una velocitat inicial de 34.2 km/h i un angle de 39.8º respecte a l'horitzontal. La incertesa de l'altura és 0.3 m, de la velocitat, 0.6 km/h i de l'angle, 0.2º. Amb l'acceleració de la gravetat g = 9.80 m/s² i negligint la fricció amb l'aire, determina

a) l'altura màxima de la pilota sobre el terra;

b) la distància recorreguda horitzontalment fins que toca terra per primera vegada.

Considerem un sistema de coordenades cartesianes amb origen en el peu de la torre. La posició de la pilota en funció del temps serà

x(t) = v₀ cos(α) t,

La velocitat serà

v_x(t) = v₀ cos(α),

v_y(t) = v₀ sin(α) – g t.

Els valors númerics de h, v₀ i α són

h = 17.9 ± 0.3 m,

v₀ = 34.2 ± 0.6 km/h = 9.500 ± 0.166 m/s,

α = 39.8º ± 0.2° =  0.69464 ± 0.00349 rad.

Les incerteses de la velocitat i l'angle s'han escrit amb tres xifres significatives perquè no són resultats finals.

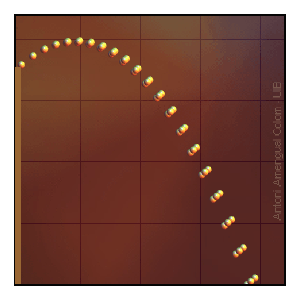
Figura 1. Posicions de la pilota a intervals de temps regulars per a tres velocitats inicials lleugerement diferents.

La pilota arriba a l'altura màxima quan la velocitat v_y s'anul·la. Això passa per a un temps t₁ solució de

v_y(t₁) = v₀ sin(α) – g t₁ = 0.

d'aquí s'obté

L'altura màxima A és y(t₁). Fent les operacions s'obté

La incertesa serà

a) Altura màxima = 19.8 ± 0.4 m  

La pilota arriba a terra quan y(t) s'anul·la. Això passa per a un temps t₂ tal que

La solució cercada és

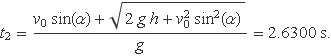
La incertesa d'aquest temps és

amb

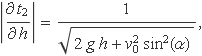
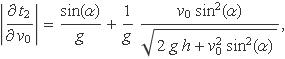
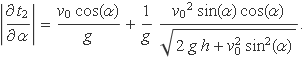
La incertesa del temps t₂ és 0.0329 s, per tant

t₂ = 2.63 ± 0.03 s.

Durant aquest temps, la pilota es mou horitzontalment una distància

Per calcular la incertesa d'aquesta distància, s'ha d'estar alerta, perquè t₂ depèn de h, v₀ i α. S'ha de considerar

i calcular la incertesa amb l'expressió

Es tendrà

Les derivades de t₂ respecte de h, v₀ i α s'han calculat abans. S'obté així

b) Distància horitzontal fins a terra = 19.2 ± 0.6 m