A la presentació de la distribució de Poisson s'escrigué que el nombre de partits en els mundials amb un determinat nombre de gols es podia aproximar amb aquesta funció i les dues taules d'aquell apartat en donaven una prova qualitativa. Si bé els números reals i els del model coincidien bastant bé, la comparació s'ha de fer quantitativament. La funció densitat de probabilitat khi quadrat (χ²) presentada en aquest bloc de temes serveix per analitzar la probabilitat que unes dades es distribueixin segons alguna distribució teòrica.

Després de presentar la funció densitat de probabilitat χ² es presentarà el test del mateix nom i s'aplicarà i) per analitzar si uns daus estan trucats, ii) per comprovar que la comparació entre els gols marcats i els generat per la distribució de Poisson és matemàticament bona i iii) per comprovar si un conjunt de valors aleatoris es poden descriure amb una distribució gaussiana.

Especialment en casos semblants al tercer s'ha de tenir present que algunes vegades, l'anàlisi del fenomen que genera les dades numèriques serveix per definir la funció de probabilitat, però altres vegades les dades s'usen per establir una funció de probabilitat teòrica que les pot descriure i, a partir d'ella, fer algun tipus d'anàlisi. Però si en aquest segon cas el nombre de dades és petit, hi pot haver més d'una funció de probabilitat que sembli descriure la seva distribució. A la Fig. 1 es mostra una gaussiana i una altra funció de distribució que té la mateixa mitjana i la mateixa desviació estàndard (és l'anomenada funció gamma). Les dues corbes són semblats i si no es té un conjunt de molts de punts segurament aquest conjunt passarà el test χ² per a les dues: Les dues funcions densitat de probabilitat podrien servir per descriure-les. Com més semblants siguin les funcions, més dades són necessàries perquè es puguin distingir.

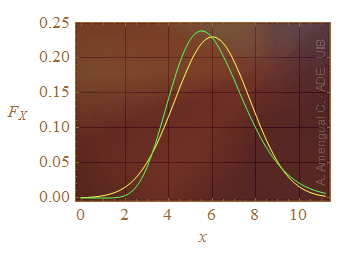
Figura 1. Gràfics de la funció densitat de probabilitat gaussiana (línia groga) i de la funció densitat de probabilitat gamma de la mateixa mitjana i desviació estàndard que la gaussiana (línia verda).