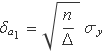Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Ajusts per mínims quadrats
Errors sobre els coeficients de la recta d'ajust
Introducció «
Les expressions que donen els coeficients a0 i a1 de l'ajust y = f(x) = a1 x + a0 són

Les sumes Sx, Sx2 i Δ només depenen de les abscisses xi i es coneixen exactament. Per tant, només s'ha de determinar la propagació de la incertesa σy de les ordenades yi on
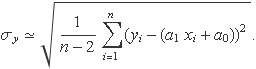
Incertesa sobre el terme independent «
L'expressió que dóna el coeficient a0 es pot escriure de la manera següent:
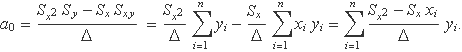
El coeficient a0 és una combinació lineal dels valors yi,
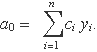
Escrita l'expressió de a0 així, la incertesa és directament
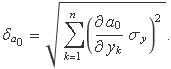
Si es té present que la incertesa sobre les ordenades és la mateixa, es pot extreure factor comú,
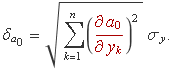
La derivada parcial dóna
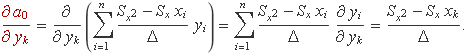
L'expressió de l'error és
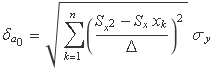
Elevant el terme entre parèntesis al quadrat
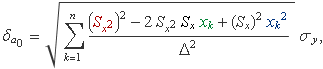
i fent les sumes es tendrà: i) En sumar el terme vermell, que és un número, sortirà n vegades aquest número; ii) en sumar xk (terme verd), sortirà el valor de Sx com el que ja hi ha; i iii) en sumar xk2 (terme blau), sortirà la suma Sx2. Per tant,
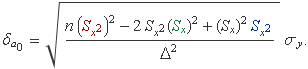
El tercer terme del numerador anul·la el 2 del segon terme i queda
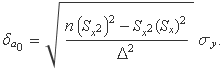
El numerador és Sx2 multiplicat per n Sx2 – (Sx)2, que és Δ,
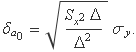
Simplificant, s'obté finalment
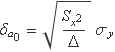
Incertesa sobre el pendent
 «
«
L'expressió que dóna el coeficient a1 es pot escriure de la manera següent:
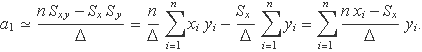
El coeficient a1 és una combinació lineal dels valors yi,
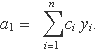
Escrita l'expressió de a1 així, la incertesa és directament
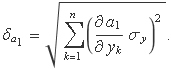
Si es té present que la incertesa sobre les ordenades és la mateixa, es pot extreure factor comú,
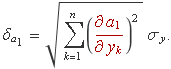
La derivada parcial dóna
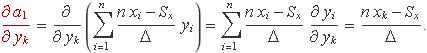
L'expressió de l'error serà
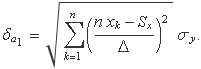
Elevant el terme entre parèntesis al quadrat
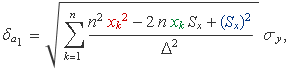
i fent les sumes es tendrà: i) En sumar el terme vermell, sortirà la suma Sx2; ii) en sumar xk (terme verd), sortirà el valor de Sx com el que ja hi ha; i iii) en sumar el terme blau, que és un número, sortirà n vegades aquest número. Per tant,
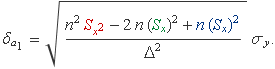
El tercer terme del numerador anul·la el 2 del segon terme i queda
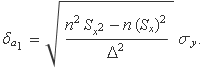
El numerador és n multiplicat per n Sx2 – (Sx)2, que és Δ. En conseqüència