
Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Distribucions de probabilitat
Definicions
Llista ordenada conceptualment «
Es recull la notació usada de manera habitual, però no exclusiva, per indicar diversos termes que aparèixen en el text.
Espai mostral, població o univers Ω
 «
«
Conjunt dels possibles valors que pot tenir una variable aleatòria. Per a cada tipus de procés aleatori es tendrà un univers. S'indicarà amb la lletra omega majúscula, Ω.
Ω : (Omega) Espai mostral, població o univers d'una variable aleatòria genèrica.
ΩX : Univers d'una variable aleatòria anomenada X.
L'univers de la suma dels punts resultants en el llançament de dos daus és
Ω = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
Variable
 «
«
Magnitud que pot tenir un valor qualsevol dels compresos en un conjunt.
Una variable r igual a qualsevol número real (r ∈ R).
Una variable k igual a qualsevol número sencer (k ∈ Z).
Una variable v igual a una lletra (v ∈{a, b, c, ..., y, z}).
Variable discreta
 «
«
Variable que pren valors en un conjunt numerable (conjunt que es pot posar en correspondència biunívoca amb el conjunt o un subconjunt del números sencers).
Una variable v que pot ser igual a una lletra és discreta.
Variable continua
 «
«
Variable que pren valors en un conjunt tal que entre dos possibles valors sempre n'hi ha infinits més.
Una variable r que pot ser igual a un número real és continua.
Variable aleatòria
 «
«
Magnitud que pot tenir un valor qualsevol a l'atzar dels compresos en un conjunt Ω que s'anomenarà univers. Per definir una variable aleatòria s'ha d'especificar l'univers i la probabilitat que la variable aleatòria prengui un valor d'aquest univers.
Sigui X la variable aleatòria que pren un valor de l'univers Ω = {cara, creu} com a resultat del llançament d'una moneda voltejada en l'aire, la probabilitat de cada resultat és 1/2. En aquest exemple la variable aleatòria és discreta.
Sigui X la variable aleatòria continua Ω ∈ R de l'interval de temps entre l'arribada de dues partícules de la radiació de fons a un comptador Geiger.
Variables independents
 «
«
Dues varirables aleatòries són independents si el valor que prengui una variable no limita el valor que pugui prendre l'altra.
Per a dues variables independents X i Y, la probabilitat que X = x0 i Y = y0 és la probabilitat que X = x0 multiplicada per la probabilitat que Y = y0.
Probabilitat Pr(A)
 «
«
La notació Pr(A) no representa una funció estrictament, s'usa per poder incloure dins les fórmules la frase «probabilitat que succeeixi A», on A pot ser, per exemple, «resultat igual a 2», «resultat més gran que 2»...
En un context on hi hagi definida una o més variables aleatòries X, Y..., Pr(xi) o Pr(xi, yi) seran notaciona compactes on A s'ha d'interpretnar per «resultat X = xi») i «resultat X = xi i Y = yi», respectivament.
Distribució de probabilitat FX(x)
 «
«
La distribució de probabilitat per a una variable aleatòria X és la funció FX(x) que dóna la probabilitat que X sigui menor o igual que x,
FX(x) = Pr(X ≤ x)
En anglès s'usen les sigles CDF per cumulative distribution function i es pot traduir per funció de distribució acumulada.
La distribució de probabilitat per a una variable aleatòria discreta només es pot definir si es té definida una funció per ordenar els elements de l'univers Ω.
Sigui X la variable aleatòria que pren un valor aleatori dins l'interval (0, a) amb igual probabilitat. La distribució de probabilitat és la funció
>FX(x) = Pr(X ≤ x) = x/a.
Funció de probabilitat PX(ν)
 «
«
La funció de probabilitat per a una variable aleatòria discreta X és la funció PX(ν) que dóna la probabilitat pν que X sigui igual a ν,
P(ν) = Pr(X = ν) = pν.
Sigui X la variable aleatòria igual al nombre de punts que s'obtenen al llançar un dau sense trucar. L'únivers té sis elements, Ω = {1, 2, 3, 4, 5, 6} i qualsevol puntuació pot sortir amb la probabilitat p1 = p2 = ... = p6 = 1/6.
Funció de probabilitat binomial
 «
«
La funció de probabilitat binomial Bn,p(k) dóna la probabilitat de tenir k resultats d'èxit quan es fan n experiments, cada un dels quals té una probabilitat d'èxit p.
![]()
Funció de probabilitat de Poisson
 «
«
Sota determinadades condicions, si en mitjana es donen μ successos d'un tipus en un interval de temps o d'espai fixat, la probabilitat que es donin k sucessos en un interval determinat és
![]()
Densitat de probabilitat PX(x)
 «
«
La densitat de probabilitat per a una variable aleatòria continua X és la funció
![]()
de manera que usant la lletra grega ξ per indicar la variable d'integració
![]()
En anglès s'usen les sigles PDF per probability density function i es pot traduir per funció densitat de probabilitat. Cal notar que la sigla D de PDF no té el mateix significat que la D de CDF (cumulative distribucion function) amb que s'anomena la distribució de probabilitat.
Sigui X la variable aleatòria que pren un valor aleatori dins l'interval (0, a) amb igual probabilitat. La densitat de probabilitat és PX(x) = 1/a.
Densitat de probabilitat normal o gaussiana
 «
«
La funció de probabilitat de Gauss, anomenada normal o gaussiana, de mitjana μ i variància σ2 és
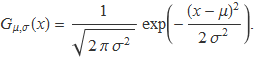
Valor esperat
 «
«
El valor esperat s'indica amb E(X), E(X, Y)
Valor esperat d'una variable aleatòria
 «
«
Si X és una variable aleatòria discreta, el valor esperat d'una funció u(X) és
![]()
Si X és una variable aleatòria continua, el valor esperat d'una funció u és
![]()
Si f(X) = c, una constant, el valor esperat és c perquè la suma de les probabilitat pν o la integral de la densitat de probabilitat val 1. El valor esperat d'una constant és la constant.
Si f(X) = X, el valor esperat és la mitjana poblacional.
Si la funció f(X) = a g(X) + b h(X), on a i b són constants, llavors resultarà ![]() L'operador valor esperat és lineal.
L'operador valor esperat és lineal.
Valor esperat de dues variables aleatòries
 «
«
Per a dues variables aleatòries X i Y discretes definides sobre el mateix univers, el valor esperat d'una funció u(X, Y) és, simbólicament,
![]()
Si X i Y són variables aleatòries continues, el valor esperat d'una funció u(X, Y) és, simbòlicament,
![]()
Mitjana poblacional μ
 «
«
La mitjana poblacional és el valor esperat de la funció identitat de la variable aleatòria X. Per a variables discretes i continues es calcula amb les expressions
![]()
![]()
respectivament. La suma es fa sobre tots els valors de l'univers i la integral, sobre el domini de l'univers. El valor de la mitjana poblacional s'indica amb la lletra μ:
![]()
Variància poblacional σ2
 «
«
La variància poblacional és el valor esperat de la funció (X – μ)2. Per a variables discretes i continues es calcula amb les expressions
![]()
![]()
respectivament. El valor de la variància poblacional s'indica amb la lletra σ al quadrat.
![]()
La variància d'una combinació lineal de variables aleatòries independents,
![]()
és
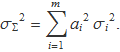
Desviació estàndard σ
 «
«
Arrel quadrada de la variància.
Mostra
 «
«
Un subconjunt de la població.
Estimador estadístic
 «
«
Un estimador estadístic és un valor calculat a partir d'una mostra per descriure una propietat desconeguda de la població Ω. Per exemple, la mitjana d'una mostra és un estimador de la mitjana poblacional. Una propietat θ indeterminada de la població pot tenir més d'un estimador estadístic (cal notar que al canviar la mida de la mostra, l'estimador estrictament ja és diferent). Genèricament, l'estimador de la propietat θ s'escriu ![]() .
.
Biaix
 «
«
Sigui ![]() un estimador estadístic d'una propietat de valor θ d'una població Ω. L'estimador estadístic es calcula a partir d'una mostra. El biaix de l'estimador estadístic és
un estimador estadístic d'una propietat de valor θ d'una població Ω. L'estimador estadístic es calcula a partir d'una mostra. El biaix de l'estimador estadístic és
![]()
Si el biaix d'un estimador estadístic és nul, es diu que l'estimador no té biaix.
Un estimador estadístic per a la mitjana poblacional (θ = μ) és la mitjana d'una mostra. El biaix d'aquest estimador és 0.
Mitjana d'una mostra ![]()
 «
«
La mitjana d'una mostra de n valors {x1, x2, x3 ..., xn}és
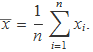
La mitjana d'una mostra de n valors d'una variable aleatòria X és un estimador estadístic sense biaix de la mitjana poblacional μ.
Variància de la mostra sN2 esbiaixada
 «
«
Per a una conjunt de n valors {x1, x2, x3 ..., xn}, l'expressió
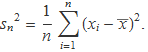
no és un estimador estadístic apropiat de la variància poblacional perquè el biaix no és nul.
Variància de la mostra sN2 sense biaix
 «
«
La variància sense biaix d'una mostra de n valors {x1, x2, x3 ..., xn}és
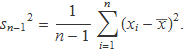
La variància sense biaix d'una mostra de n valors d'una variable aleatòria X és un estimador estadístic de la variància poblacional.
Variància de la mitjana de la mostra
 «
«
Una mostra de n elements de Ω es pot considerar com si fos una mostra de 1 element de cada una de n variables Xi. La variància de la variable aleatòria
![]()
equival a la variància de la mitjana dels n elements. Usant la variància d'una combinació lineal de variables aleatòries,
![]()
amb ai = 1/n, es té
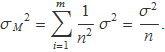
Error estàndard de la mostra
 «
«
L'error estàndard d'una mostra de n elements de Ω és la desviació estàndard de la mitjana de la mostra
![]()
