Curs ADE: CorrLin1

Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.

Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.

Exercicis i problemes

Ajust per mínims quadrats / 1r^model

1. Variances i covariància de dues variables «

La taula següent dóna n = 6 mesures de dues variables amb unitats arbitràries

$x$	18.9895	17.4806	18.0637	19.0089	19.6577	18.1229
$y$	14.215	13.4907	13.7706	14.2243	14.5357	13.799

a) Calcula les variances de x i y i la covariància

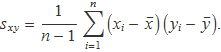
"ade_1.gif"

b) Donada la funció

q(x, y) = $\frac{y^{2}}{2 x + 10}$

determina la sèrie de Taylor a primer ordre en el punt . Calcula els valors de q per als punts (x, y) de la taula amb la funció donada i amb la sèrie de Taylor determinada.

c) Calcula la desviació estàndard de la variable q a partir dels valors q_i(x_i, y_i).

d) Calcula ara la desviació estàndard de q usant la fórmula general

i compara amb el resultat obtingut a l'apartat anterior.

e) Escriu els valors mitjans de x, y i q amb l'error estàndard i el nombre de xifres significatives adient.

Solució »

a) s_xy = 0.31.

c) s_q = 0.09.
d) s_q = 0.09.
e) $\overline{x}$ = 18.6 ± 0.3,
$\overline{y}$ = 14.01 ± 0.16,
$\overline{q}$ = 4.16 ± 0.04

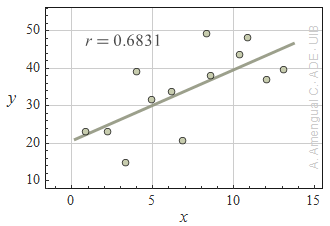
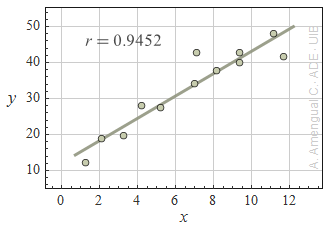
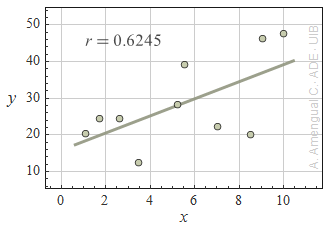
2. És la correlació lineal significativa? «

En els gràfics següents es mostra un conjunt de punt, la recta que els ajusta per mínims quadrats i el coeficient de correlació lineal r. Determina en cada cas si la correlació lineal entre les variables x i y és significativa o molt significativa.

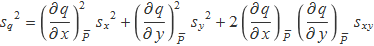
"ade_4.gif"

Solució »

"ade_5.gif"

Solució »

"ade_6.gif"

Solució »

"ade_7.gif"

Solució »

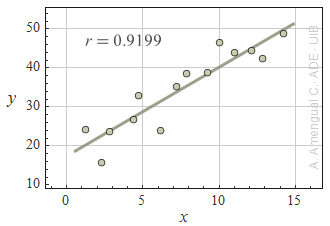
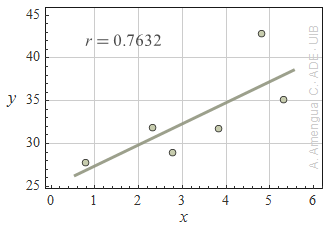
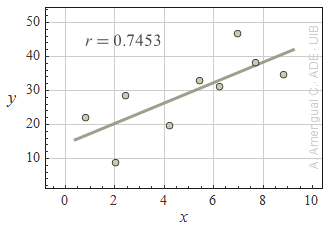
"ade_8.gif"

Solució »

"ade_9.gif"

Solució »

"ade_10.gif"

Solució »