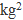Anàlisi de Dades Experimentals
© Antoni Amengual Colom. Departament de Física, Universitat de les Illes Balears.
Versió 1.0 publicada al setembre de 2013. DL: PM 860-2013.
Exercicis i problemes
Ajust per mínims quadrats / 2n model
1. Ajust recta que passa per l'origen
 «
«
a) Determina amb tres decimals el coeficient a de la recta y = a x que ajusta per mínims quadrats els punts
| x | y |
| 3.9 | -0.53 |
| 8.2 | -1.16 |
| 12.2 | -1.46 |
| 16.3 | -2.10 |
| 20.5 | -2.52 |
| 24.5 | -3.58 |
b) Fes un gràfic amb els punts i la recta que els ajusta.
Solució »
2. Ajust rectilini
 «
«
a) Determina amb tres decimals els coeficients a i b de la recta y = a x + b que ajusta per mínims quadrats els punts (x, y) de la taula.
| x (kg) | y (Pa) |
| 3.0 | 0.4 |
| 5.9 | 0.8 |
| 9.1 | 1.1 |
| 12.1 | 1.4 |
| 14.9 | 1.6 |
b) Fes un gràfic amb els punts i la recta que els ajusta.
Solució »
3. Ajust parabòlic
 «
«
a) Dedueix les expressions que donen els valors de les constants a i b que minimitzen la suma S de les distàncies al quadrat de n punts Pi = (xi, yi) a la corba y = a x2 + b.
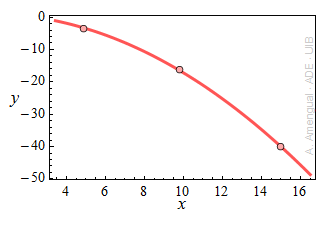
b) Determina la corba y = a x2 + b que ajusta per mínims quadrats els punts (4.9, -3.5), (9.8, -16.2) i (15.0, -40.1). Dóna les constants a i b amb tres decimals.
c) Fes un gràfic amb els tres punts i la corba que els ajusta.
Solució »
4. Elongació d'una molla
 «
«
Considera una molla de constant elàstica k, longitud natural s0 i massa negligible. La molla tendrà una longitud x més gran que la natural quan es penji d'un punt fix i s'estiri pel pes d'una massa m. La força recuperadora és igual al pes quan la massa no es mou i es compleix la relació
k (s – s0) = m g,
on s – s0 és l'elongació de la molla i g, l'acceleració de la gravetat.
Es disposa de masses diverses i s'usen per mesurar la longitud de la molla sotmesa a pesos diferents.
a) Segons la relació donada, quin serà el pendent de la recta s(m)?
b) A la taula adjunta es donen els valors de l'elongació mesurada amb 5 masses penjades diferents. Què val la suma dels productes si mi?
| 0.156 | 0.425 |
| 0.302 | 0.484 |
| 0.537 | 0.574 |
| 0.670 | 0.628 |
| 0.826 | 0.686 |
c) Què val la suma dels quadrats de les masses? (Aquesta suma i l'anterior es necessiten per respondre l'apartat següent.)
d) Determina el valor del pendent de la recta que ajusta els punts per mínims quadrats i fes un gràfic dels punts amb la recta s(m)
e) Usa g = 9.80 m/s2 per determinar la constant elàstica de la molla en N/m.
f) Quina és la longitud natural en cm de la molla segons les mesures fetes?
g) Determina per mínims quadrats el pendent de la recta que ajusta els punts xi ≡ si, yi ≡ mi g i verifica que és igual a k.
Nota: Dóna els resultats demanats amb tres xifres decimals.
Solució »
5. Cal·librar un termòmetre
 «
«
La resistència d'un filament metàl·lic augmenta amb la temperatura. Aquest fet permet construir termòmetres basats en la mesura de la resistència del filament. S'ha mesurat la resistència d'un filament a 7 temperatures conegudes. Els resultats han estat els de la taula.
| T (K) | R (Ω) |
| 277.62 | 21.3862 |
| 287.15 | 25.8793 |
| 299.61 | 29.6113 |
| 315.27 | 34.4903 |
| 333.09 | 38.0947 |
| 358.75 | 42.9429 |
| 392.35 | 47.3963 |
a) Determina els coeficients de la funció T (K) = a2 R2 + a1 R + a0 amb R expressat en ohms, que ajusta els valors mesurats per mínims quadrats.
b) Quina és la temperatura del filament si R = 35.2515 Ω?
c) I si R = 39.0751 Ω?
Solució »