Trajectòries dins camps gravitatoris (1)
Quan sigui necessari usar la gravetat a la superfície terrestre, s'usarà g = 9.80 m/s2. La constant gravitatòria s'ha de saber almenys amb l'aproximació
G = 6.67 10 − 11 N m2 kg − 2.
Altres valors necessaris per resoldre els problemes, la massa i el radi de la Terra per exemple, es donaran amb l'enunciat.
Lleis de Kepler 


Johannes Kepler (1571-1630), astrònom i matemàtic alemany. Va descobrir les lleis sobre el moviment dels planetes. Les seves obres més influents varen ser Astronomia Nova i Harmonices Mundi.

• Enunciar les lleis de Kepler, interpretar-les i resoldre problemes amb la tercera llei.
1
El semieix de l'òrbita de Júpiter és 5,204 vegades més gran que el de l'òrbita de la Terra. Quants d'anys tarda Júpiter en fer una volta al Sol d'acord amb la tercera llei de Kepler?
2

De les quatre llunes de Júpiter que va descobrir Galileu el 1610, Ió és la més pròxima al planeta i Cal·listo, la més llunyana. L'òrbita de Cal·listo té un període de 400.6 hores i el semieix més gran mesura 1882700 km. L'òrbita d'Ió té un període de 42.5 hores, què mesura aproximadament el semieix de l'òrbita d'Ió?
3
Un planeta es mou al voltant d'una estrella en una òrbita circular amb un període de 2.5 anys. Quin és el període d'un altre planeta d'aquest sistema solar que té una òrbita 5 vegades més lluny de l'estrella?
Trajectòria radial 



• Aplicar el principi de conservació de l'energia mecànica per determinar la velocitat o la posició d'un objecte que es mou radialment.
• Calcular si un objecte llançat en direcció radial des d’un planeta pot arribar a una determinada distància i fins a quina distància arriba abans de tornar cap el planeta, negligint l'efecte gravitatori d'altres planetes i llunes.
4
Una sonda a Venus té una velocitat de 2.37 km/s a 9100 km del centre del planeta. Quina serà la velocitat de la sonda a 7000 km?
MVenus = 4.867 1024 kg. El canvi d'energia potencial gravitatòria respecte del Sol és molt petit i es pot negligir.
5
Des de la superfície de la Terra es llança un objecte verticalment amb una velocitat de 1200 km/h. Negligint la fricció amb l'aire i suposat que l'acceleració de la gravetat val 9.823 m/s2 durant tot el recorregut, fins a quina altura màxima arriba l'objecte?
6
Repeteix el problema 5 tenint en compte la variació de l'atracció gravitatòria amb l'altura.
MT = 5.972 1024 kg, RT = 6370 km.
7
Apagats els propulsors, una sonda espacial s'allunya radialment de la Terra. A 72000 km de la Terra es mou a 3 km/s. Fins a quina distància màxima de la Terra arribarà?
MT = 5.972 1024 kg.
Velocitat d'escapament 



• La definició de velocitat d’escapament d’un objecte i saber calcular-la a partir del principi de conservació de l’energia mecànica quan l’objecte està inicialment a la superfície d’un cos massiu sense rotació o a certa distancia del centre de masses del cos massiu.
8
Quina velocitat mínima ha de tenir una sonda quan està a 2 105 km d'una estrella de 5 1030 kg per allunyar-se indefinidament d'ella sense propulsió?
Òrbites circulars 


• Calcular les característiques de les òrbites circulars d’un objecte en un camp gravitatori.
• Les relacions entre les energies potencial Ep, cinètica Ec i total ET per a una òrbita circular i com s'obtenen aquestes:
Ec = −Ep/2,
ET = Ec + Ep = Ep/2.
• Calcular el radi i l'altura d'una òrbita estacionària. Distingir entre altura i radi de l'òrbita.
9
L'energia potencial gravitatòria d'un satèl·lit en òrbita circular al voltant de la Terra val −5.4 1010 J. Què val l'energia cinètica del satèl·lit?
10
Un satèl·lit en òrbita circular té una energia mecànica total de −6.4 1010 J. Què val l'energia potencial gravitatòria del satèl·lit?
11
L'energia cinètica d'un satèl·lit de 1210 kg en òrbita circular al voltant de la Terra val 2.41 1010 J. Quin és el radi de l'òrbita?
MT = 5.972 1024 kg.
12
Una òrbita geostacionària és una òrbita circular dins el pla equatorial caracteritzada perquè el període orbital és igual al període de rotació de la Terra. Un satèl·lit en òrbita geostacionària està sobre un mateix lloc de la Terra. Què val l'altura de l'òrbita geostacionària?
MT = 5.972 1024 kg, RT = 6370 km.
13
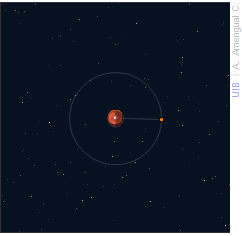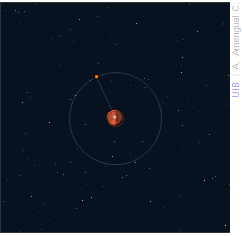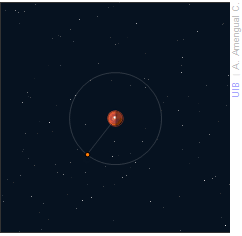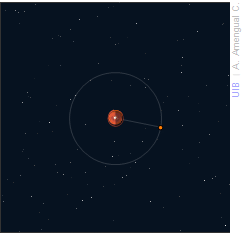
La figura adjunta mostra Mart i l'òrbita estacionària al voltant seu a la mateixa escala que la Terra i l'òrbita geostacionària a la figura de l'exercici 12. Calcula a partir de lleis físiques el radi de l'òrbita estacionària al voltant de Mart. Què val l'altura d'aquesta òrbita?
Actualment no hi ha cap satèl·lit en òrbita estacionària al voltant de Mart però ja s'ha donat nom a l'òrbita. El nom de l'òrbita i la justificació es mostrarà quan s'hagi contestat correctament la pregunta (i es relacionarà amb Wonder Woman).
Dades del planeta Mart: Massa = 6.417 1023 kg; Radi = 3396 km; Període de rotació = 24 h 37 min.
14
Un objecte de 2400 kg en òrbita circular al voltant d'un planeta de 6 1024 kg té una energia potencial de −1.91 1012 J. La velocitat de l'objecte és constant i tangent a la circumferència de l'òrbita. Si la velocitat canviés a radial, fins a quina distància màxima del planeta arribaria?
15
La lluna més gran del sistema solar té una massa de 1,482 1023 kg i una òrbita al voltant del seu planeta que es desvia poc d'una circumferència de radi 1,07 106 km i es completa en 7 dies i 3.6 hores.
En un examen, no es pot demanar quina és aquesta lluna ni al voltant de quin planeta orbita (saber les llunes del sistema solar no entra en el temari). Però amb dues de les tres dades numèriques presentades és possible calcular la massa del planeta, llavors en un examen sí que es podria demanar aquesta massa. Quina és la massa del planeta? Fixa't que la solució s'ha de donar usant la massa de la Terra com a unitat (en haver obtingut la massa en kg, divideix el valor per la massa de la Terra). Els noms de la lluna i el planeta es podran veure després d'haver contestat correctament.
MT = 5.972 1024 kg.

 Temes
Temes  Portada
Portada  Olimpíada
Olimpíada 