Camp gravitatori

Una càrrega puntual

El treball és un concepte físic que relaciona el desplaçament a velocitat constant (o amb acceleració zero) d'un objecte i una força aplicada sobre l'objecte.
El treball es defineix matemàticament de manera que només es té en compte la component de la força en la direcció del desplaçament. Per això, es multiplica la força pel desplaçament i pel cosinus de l'angle α que formen la força aplicada sobre la partícula amb càrrega elèctrica i la direcció del desplaçament.
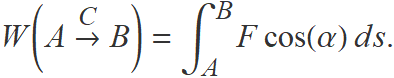
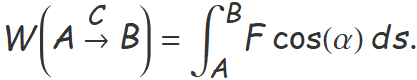
S'ha de distingir el treball del camp elèctric del treball d'una força externa quan es mou una càrrega dins un camp elèctric.
El treball del camp elèctric Wcamp és el treball que fa la força que apareix sobre una partícula amb càrrega elèctrica dins un camp elèctric.
El treball de la força externa és el treball que fa una força aplicada a una partícula dins un camp elèctric perquè es mogui a velocitat constant. la força externa anul·la la força elèctrica perquè no hi hagi acceleració. Al llarg del mateix desplaçament, la força externa sobre una partícula carregada elèctricament té sentit contrari a la força elèctrica. Els treballs serán iguals en mòdul, però de signe contrari:
WFext(A→B) = −Wcamp(A→B)
Quan l'angle α estigui entre 0 i menys de 90°, el treball serà positiu (perquè el cosinus de l'angle ho és positiu).
Quan l'angle α estigui entre més 90° i 180°, el treball serà negatiu (perquè el cosinus de l'angle és negatiu).
Quan l'angle α sigui de 90°, la força no fa treball: El treball és zero.

En el desplaçament radial des de Q d'una càrrega q des d'una distància rA fins a una rB, el treball fet pel camp eléctric de Q s'ha de calcular amb una integral perquè la intensitat del camp canvia
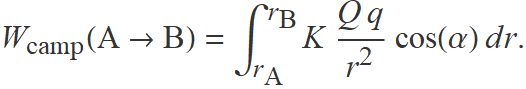
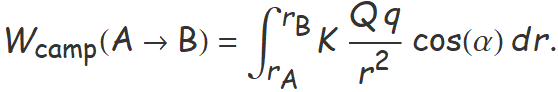
En aquesta expressió no hi ha el signe menys davant la integral que surt a l'expressió de Wcamp(A→B) del camp gravitatori perquè les càrregues tenen signe. Quan q té signe contrari a Q, s'atreuen com les masses i l'integrand és negatiu.
L'angle α és zero perqué el camp i el desplaçament són paral·lels. Amb cos(0) = 1, el treball s'obtindrà integrant 1/r2 que és −1/r. Després d'imposar els límits d'integració queda
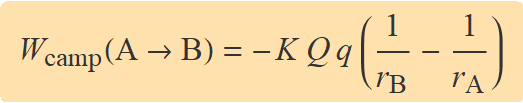
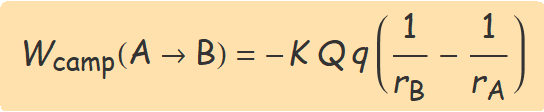
Els valors numèrics de Q i q s'han d'expressar amb el seu signe per calcular el treball.

Per moure una partícula carregada dins un camp elèctric sense acceleració, la força externa ha de cancel·lar la força elèctrica i, per tant, ha de tenir sentit contrari a aquesta força. Els treballs tenen signes contraris
WFext(A→B) = −Wcamp(A→B)
Canviant el signe al resultat Eq. (1), es té
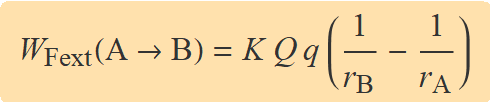
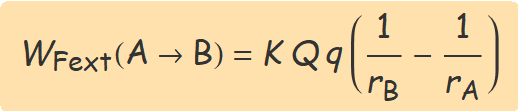
Exemple 1. Acostar dues carregues del mateix signe.
Si les càrregues s'acosten, rB < rA i rB−1 − rA−1 > 0. Llavors, atès que el producte Q q és positiu, el treball de la força externa també és positiu.
Exemple 2. Allunyar dues carregues de signe contrari
Si les càrregues s'allunyen, rB > rA i rB−1 − rA−1 < 0. Llavors, al multiplicar per Q q, que és negatiu, s'obté un resultat positiu per al treball de la força externa.

Calcular el treball realitzat per la força elèctrica o per la força externa explícitament al llarg d'un camí qualsevol entre dos punts A i B donats no és immediat, però es pot demostrar que el treball és el mateix sigui quin sigui el camí entre A i B.
WA→B no depèn del camí ⇔ Camp conservatiu

L'Eq. (1) de l'apartat «Treball fet pel camp» és
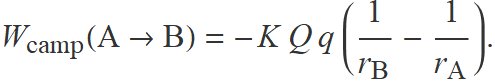
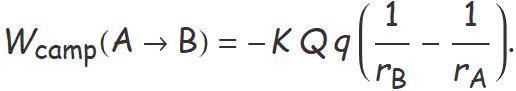
Si el punt B se situa a l'infinit, queda
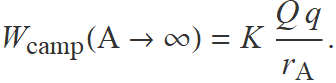
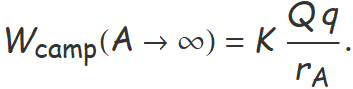
Aquest treball defineix l'energia potencial elèctrica Ep d'una partícula amb càrrega q a una distància rA de la càrrega puntual Q. Prescindint del subíndex A, es defineix
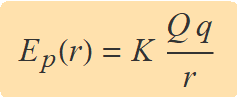
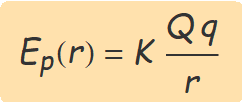
A partir de l'expressió de l'energia potencial, es defineix el potencial a una distància r com l'energia potencial d'una partícula de càrrega q,
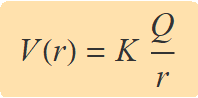
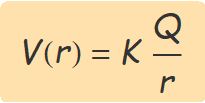
Amb aquesta definició, el treball d'una força externa per desplaçar sense acceleració una partícula amb càrrega elèctrica q entre dos punts A i B es pot determinar a partir de la diferència dels potencials en els dos punts
Wcamp(A → B) = −q (V(rB) − V(rA)).
Per simplificar la notació, es pot escriure
Wcamp(A→B) = −q (VB − VA)
El treball d'una força externa és
WFext(A→B) = q (VB − VA)
Les unitats del sistema internacional del treball són joules (J).
I les del potencial elèctric, volts (V).
Principi de superposició

El camp elèctric a causa de partícules carregades eléctricament és la suma vectorial dels camps elèctrics que causen les partícules individualment. Com a conseqüència, el potencial elèctric en un punt és la suma dels potencials elèctrics de les càrregues de les partícules.
Siguin q1, q2, q3, ... les càrregues d'unes partícules i r1P, r2P, r3P, ... les distàncies de les partícules al punt P on es vol calcular el potencial. El potencial en el punt P és la suma dels potencials elèctrics de cada partícula indiviualment,
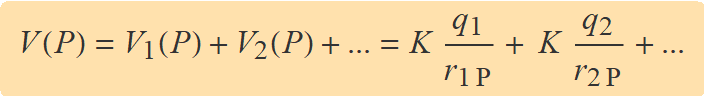
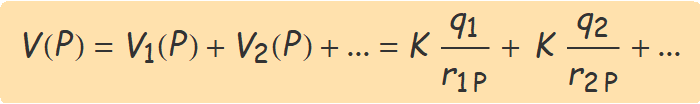
El treball del camp quan una càrrega q es mou entre dons punts A i B dins el camp elèctric d'altres càrregues és
WFext(A→B) = q (VB − VA)


A la figura següent, els cercles vermells, ●, representen partícules amb càrregues positives i el cercles negres, ●, partícules amb càrregues negatives.
Els cercles buids on apunten les fletxes mostren les posicions finals de les partícules.
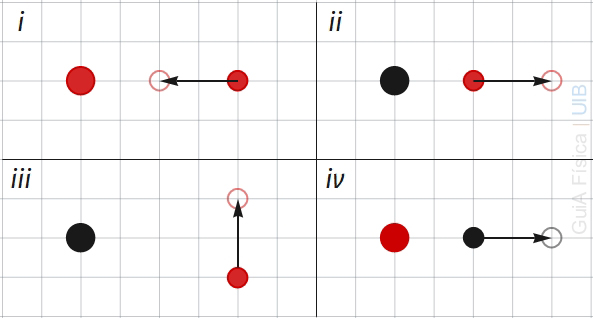
a) En un dels casos, el treball de la força externa és zero. En quin cas?
b) Justifica en cada un dels casos amb la definició de treball i els sentits de la força aplicada i el desplaçament, si el treball fet per una força externa per moure sense acceleració una partícula de la posició inicial a la final marcada pel cercle buid és negatiu, zero o positiu.
c) Calcula el treball fet pel camp en cada un dels casos si els cercles grans representen càrregues de 8 nC en valor absolut i els cercles petits, càrregues de 5 nC en valor absolut. Els quadrats del reticle tenen 1 μm de costat.
Comprova que el signe del treball del camp és el contrari del treball de la força externa determinat a l'apartat anterior.
Resolució mostrar
Sobre les figures, es dibuixen de color taronja les fletxes que representen les forces elèctriques sobre la càrrega que s'ha de moure: Repulsiva si tenen el mateix signe i atractiva si tenen signe contrari.
La força externa s'ha d'aplicar sempre en sentit contrari a la del camp perquè no hi hagi acceleració. Sobre la figura, es dibuixen de color blau les fletxes que representen les forces.
A la figura iii, també s'ha dibuixar un arc de circumferència centrat a la càrrega fixa i que passa per les posicions inicial i final de la càrrega positiva.
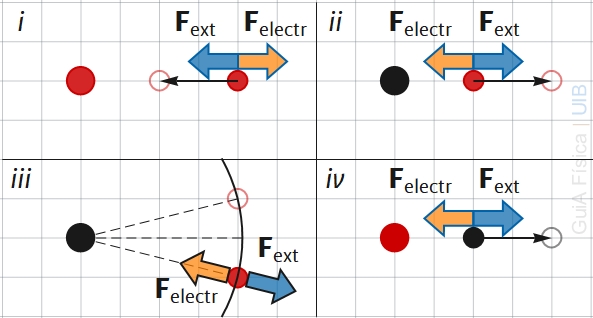

En el cas iii el treball és zero perquè les posicions inicial i final estan sobre una línia equipotencial de la càrrega fixa.
Atès que el camp és conservatiu, el treball es pot calcular a partir de la diferència de potencial entre les posicions inicial i final. Aquí, no hi ha diferència de potencial entre les dues posicions i el treball és nul.

En cada un dels casos i, ii i iv, la força externa i el desplaçament de la posició inicial a la final (marcat per la fletxa negra) tenen el mateix sentit. Per tant, el treball en els tres casos és positiu.
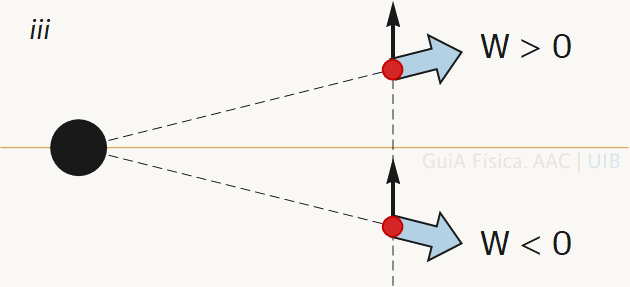
A l'apartat anterior, ja s'ha argumentat perquè el treball en el cas iii és nul. La justificacio a partir dels sentits de la força aplicada i el desplaçament és que la força externa necessària per equilibrar l'atracció sobre la càrrega positiva (vermella) és radial i el desplaçament vertical. Així, l'angle que formen la força i el desplaçament té el cosinus negatiu per baix de la línia horitzontal taronja (l'angle supera els 90°) i negatiu per damunt de la la línia horitzontal (l'angle és inferior a 90°), de manera que el treball en la primera meitat del desplaçament es cancel·la amb el treball en la segona meitat.

Les expressions per calcular el treball del camp i el treball fet per la força externa són:
Wcamp(A → B) = −q (V(B) − V(A)),
WFext(A→B)) = q (V(B) − V(A)).
S'usa aquí la segona expressió i es té:

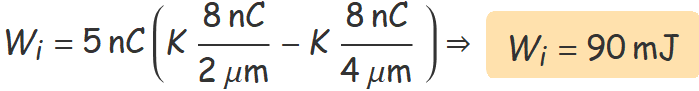
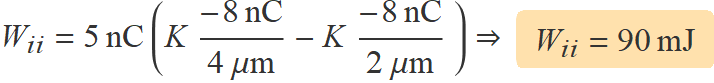
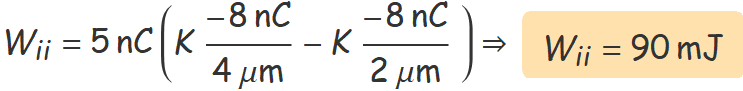
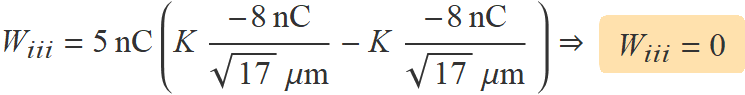

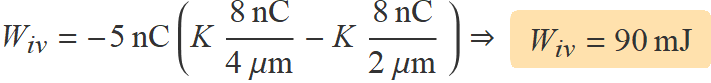
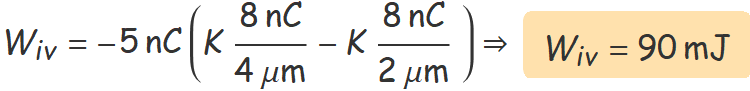
Abans de fer operacions amb la calculadora, es pot treure K factor comú i simplificar el 109 d'aquesta constant amb les potencies de 10 dels nanocoulombs i les micres.
ocultar
En un vèrtex de la base d'un quadrat d'1 m de longitud hi ha una càrrega puntual de −4 nC i a l'altre vèrtex, una de −3 nC. Calcula el potencial en el punt P en el centre del costat oposat.


Una càrrega de +2 C es desplaça sense acceleració per l'acció d'una força externa en línia recta dins el camp elèctric d'una càrrega puntual positiva Q.
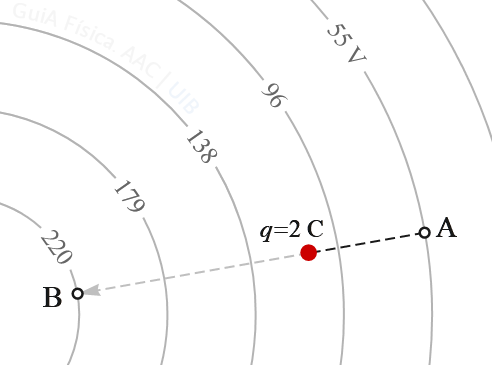
Determina el signe del treball de la força externa en el desplaçament de la càrrega des del punt A on el potencial elèctric val 55 V fins el punt B on el potencial val 220 V i quina de les afirmacions següents és certa.
a) El treball fet pel camp elèctric és positiu.
b) El treball fet per la força externa és positiu.
c) El treball fet per la força externa és negatiu.
Resposta mostrar
El signe del treball de la força externa es pot determinar de dues maneres.

El camp elèctric és conservatiu i, per definició, el treball fel pel camp es determina amb la diferència de potencial entre els punts extrems del camí:
Wcamp(A → B) = −q (V(B) − V(A)).
Així,
Wcamp(A → B) = −q (220 V − 55 V) < 0.
El treball fet pel camp és negatiu.
El treball fet per la força externa és positiu perquè
WFext(A→B) = −Wcamp(A→B).
L'afirmació correcta és la b

Es pot entendre que el treball de la força externa és positiu veient que el desplaçament d'A a B va en la direcció en que s'ha d'aplicar la força externa.
En el camp d'una càrrega Q positiva, el potencial és positiu i decreix allunyant-se de la càrrega.
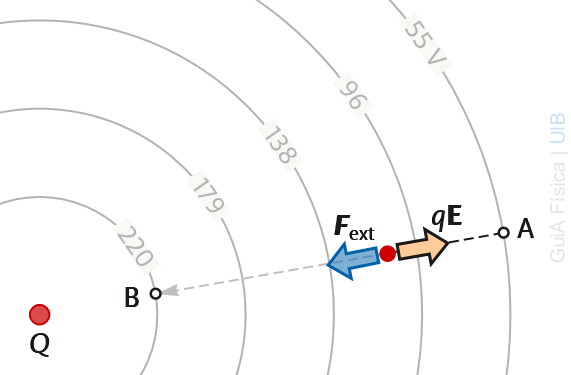
Si q es mou d'A a B a velocitat constant (és a dir, sense acceleració, com diu l'enunciat), la força externa ha d'equilibrar la força de repulsió entre càrregues positives. Per tant, ha d'apuntar radialment cap a Q i tendrà el mateix sentit que el desplaçament. Llavors, el treball és positiu.
ocultar
L'any 2015 la revista Science publicava el següent:
«Researchers have, for the first time, been able to track the movement of an electron in a molecule in real time and have demonstrated that these processes can be controlled.»
«Investigadors han pogut, per primera vegada, seguir el moviment d'un electró en una molècula en temps real i han demostrat que aquests processos es poden controlar.»
Suposant que el moviment d'un electró també es pogué dirigir, considera dues partícules molt petites carregades amb 5 mC i separades 10 μm, i un electró a 3 μm d'una d'elles com mostra la figura. Què val el treball que fa una força externa per dur l'electró del punt A al punt M?
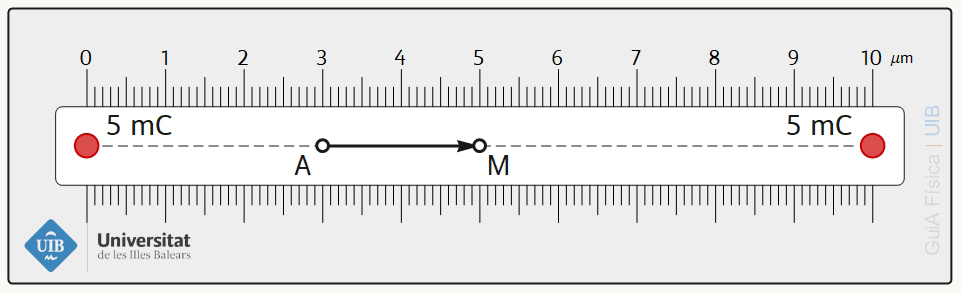


Es pot definir una funció potencial per al camp elèctric perquè és un camp és conservatiu: El treball per moure una càrrega entre dos punts dins un camp elèctric no depèn del camí seguit.

1
En una prova de l'Olimpíada nacional de Física, s'explicava el següent:
«En el año 1909 Robert Millikan y Harvey Fletcher diseñaron y realizaron el primer experimento para medir la carga del electrón. Hasta entonces los electrones sólo habían podido ser observados en forma de rayos catódicos, pero con ellos sólo se podía determinar la relación entre su carga y su masa. Con este experimento, Millikan logró medir el valor de la carga y, por tanto, también el de la masa. Para ello supuso (por aquel entonces no estaba verificado) que la carga del electrón era la fundamental y, en consecuencia, la carga de cualquier cuerpo sería un múltiplo de dicha cantidad.»OEF 2011
Millikan determinà que la càrrega de l'electró era, expresst en coulombs,
mesura de Millikan: −1.5924 × 10−19 C.
El valor establert actualment (amb incertesa en els dos darrers decimals) és
càrrega de l'electró = −1,602176487 × 10−19 C.
Calcula el potencial a 0.1 μm d'un electró segons el valor que donà Millikan per a la seva càrrega i segons el valor establert actualment.
2
Els protons es consideraren partícules elementals fins la dècada de 1960 quan s'ideà el model de quarks. En les dècades següents, amb experiments de col·lisió de partícules, es fonamentà que cada protó està format per tres quarks.
La càrrega del protó es va determinar que és igual que la de l'electró, però positiva:
càrrega d'un protó = 1,602176487 × 10−19 C.
Amb els experiments on es bombardejen protons amb electrons es determina que els protons es comporten com una càrrega concentrada en una esfera de 10−15 m. Aquí es consideren distàncies més grans i la càrrega del protó es pot tractar com a càrrega puntual. El potencial elèctric a una distància r del protó és
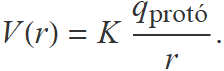
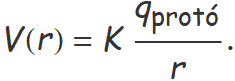
a) A quina distància r1 d'un protó el potencial elèctric és 3 mV més alt que a 150 nm del protó?
b) I a quina distància r2 el potencial és 3 mV més baix que a 150 nm?
3
Quan es frega una barra de vidre amb una tela de seda, el vidre cedeix electrons a la seda. També, quan els cabells o un jersei de llana o de cotó es frega amb un globus, se cedeixen electrons al globus i la seva superfície es carrega negativament.
Petites gotes també poden captar electrons per fregrament amb l'aire (Millikan, esmentat en el primer exercici, usà aquest fet en el seu experiment per mesurar la càrrega de l'electró). Una gota molt petita, inicialment neutra, guanya electrons i el potencial elèctric a 0.25 μm de la partícula val aproximadament −300 mV. Determina la càrrega en Coulombs que ha de tenir la gota i, després, calcula quants d'electrons ha guanyat.
4
Una petita gota neutra perd electrons. Se sap que el potencial a 0.09 μm de distància val uns 240 mV. Determina quants d'electrons ha perdut la gota.
5
El potencial elèctric en un punt a causa d'una càrrega puntual depèn de la distància entre el punt i la càrrega. El potencial al llarg d'una línia que passa per una partícula amb càrrega positiva s'ha dibuixat en el següent gràfic. La partícula està a l'origen de coordenades. Determina la càrrega elèctrica de la partícula a partir del gràfic.


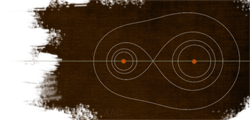
La il·lustració mostra les línies equipotencials de dues càrregues puntuals, una el doble de l'altra. A batxillerat no es demanen les equipotencials però sí calcular el potencial en un punt del pla donat, un càlcul tan senzill com és calcular les distàncies del punt a les càrregues.

6
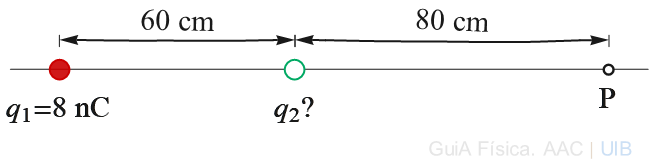
Les dues càrregues de la figura i la seva posició són iguals que les del tercer problema resolt en el tema del càlcul del camp elèctric. En aquell problema, es demanava el valor de la càrrega puntual q2 que anul·lava el camp en el punt P. Aquí es demana què ha de valer q2 perquè el potencial en el punt P sigui zero?
7
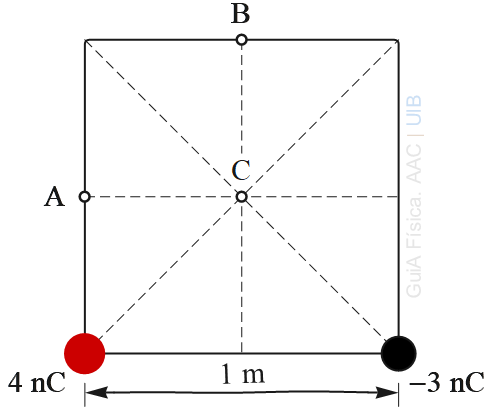
En un vèrtex de la base d'un quadrat d'1 m de longitud hi ha una càrrega puntual de 4 nC i a l'altre vèrtex, una de −3 nC. Calcula el potencial elèctric en els punts A i B, en el centre dels costats mostrats a la figura, i en el punt C, centre del quadrat.
8
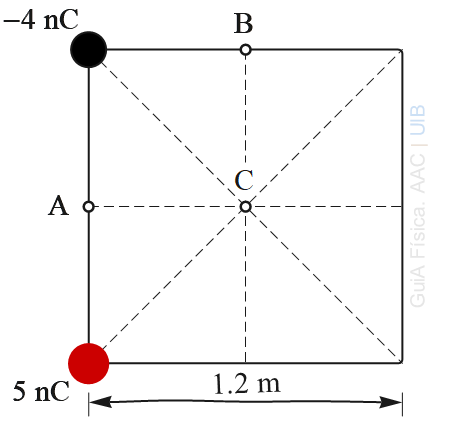
En un vèrtex del costat d'un quadrat d'1.2 m de longitud hi ha una càrrega puntual de 5 nC i a l'altre vèrtex, una de −4 nC. Calcula el potencial elèctric en els punts A i B, en el centre dels costats mostrats a la figura, i en el punt C, centre del quadrat.
9
Dues càrregues puntuals de 5 nC i $−$3 nC estan separades 2 mm. Determina a quina distància de la càrrega positiva està un punt del segment entre les càrregues on el potencial elèctric val zero.
Ajuda mostrar
L'equació que s'ha de resoldre és senzilla,
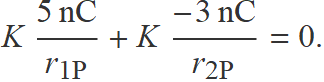
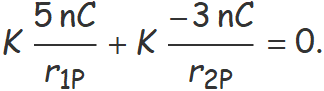
Però s'ha de tenir en compte que r1P i r2P són distàncies i el seu valor és positiu. Sigui x > 0 la distància desconeguda en mm de q1 a P, llavors
r1P = x,
r2P = 2 mm − x.
10
El potencial elèctric V(x) al llarg de la línea que passa per la posició de dues partícules amb càrregues elèctriques q1 i q2 s'ha representat gràficament. L'origen de x s'ha establert enmig de les dues partícules. Les unitats no s'han inclòs en el gràfic.
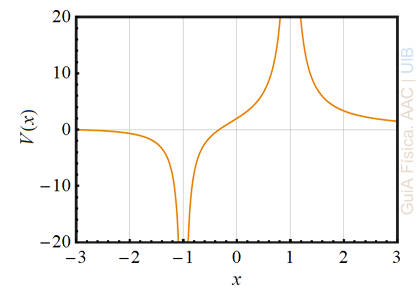
a) La partícula que té la càrrega més gran en valor absolut és la partícula de l'esquerra o la partícula de la dreta de l'origen de coordenades? Justifica la resposta.
b) Quina càrrega té la partícula de l'esquerra, positiva o negativa?


El treball fet sobre una càrrega per moure-la dins un camp elèctric o el treball fet pel camp sobre una càrrega, només depenen dels punts inicial i final del desplaçament i es poden calcular a partir de la funció potencial electrostàtic.

11
S'aplica una força a una partícula molt petita amb una càrrega elèctrica q2 positiva perquè es mogui a velocitat constant en línia recta cap una altra partícula fixa amb càrrega q1 també positiva.
a) Amb la disposició de les càrregues que mostra la figura, en quin sentit s'ha d'aplicar la força externa. Cap a l'esquerra o cap a la dreta?
b) A partir de la definició del treball d'una força, argumenta si el treball fet per la força externa és positiu o negatiu.
c) Calcula el treball fet per la força externa quan la segona partícula s'acosta de 3 μm a 2 μm de la primera partícula quan les càrregues elèctriques de les partícules són les indicades a la figura.
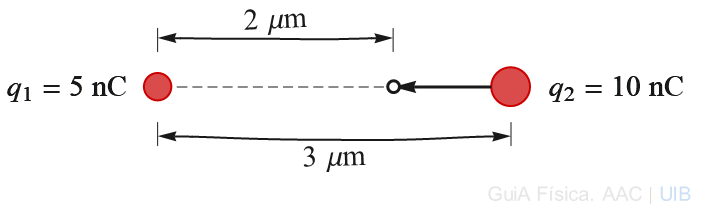
11a)
Les partícules amb càrrega positiva es repel·leixen, per tant s'ha d'aplicar una força externa cap a l'esquerra per cancel·lar la força repulsiva i què la partícula de la dreta s'acosti a la primera partícula a velocitat constant.
11b)
La força externa aplicada sobre la segona partícula i el desplaçament tenen el mateix sentit. En aquests casos, el treball és positiu.
12
a) El treball per moure una càrrega entre dos punts dins un camp elèctric es pot calcular usant una funció potencial. Quin adjectiu dels següents s'usa per als camps amb aquesta característica?
(1) escalar; (2) vectorial; (3) potencial; (4) conmutatiu; (5) associatiu; (6) cohesiu; (7) disyuntiu; (8) extensiu; (9) condensatiu; (10) constructiu; (11) conservatiu; (12) refrigeratiu; (12) transformatiu.
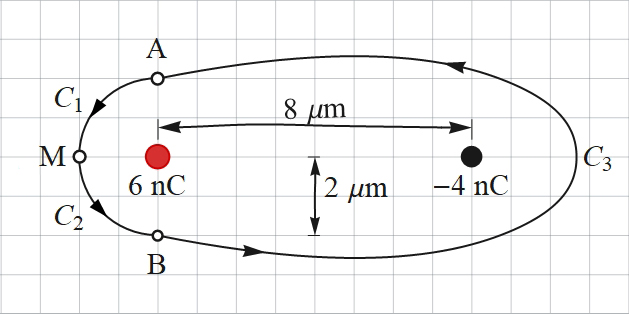
La figura representa camins entre punts dins el camp elèctric de dues partícules amb càrreges de 6 nC i −4 nC. El camins C1 entre A i M i C2 entre M i B són arcs circulars. Determina els treballs següents quan es mou una càrrega de 2.6 μC:
b) Treball del camp entre A i M al llarg del camí C1.
c) Treball del camp entre A i B seguint C1 i C2.
d) Treball d'una força externa entre M i A seguint C2 i C3.