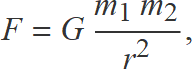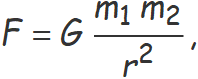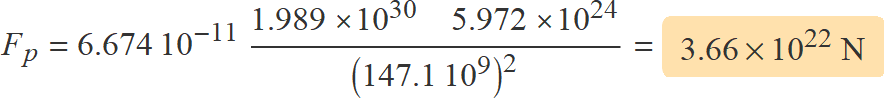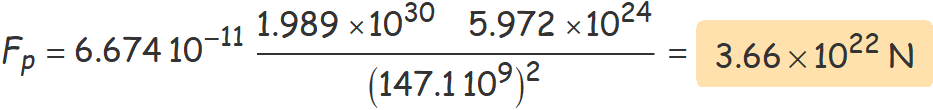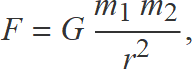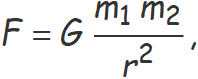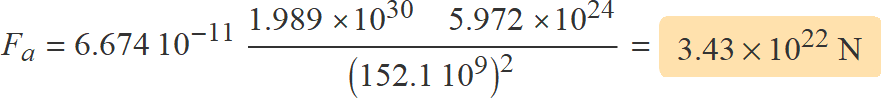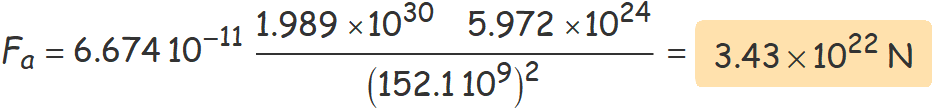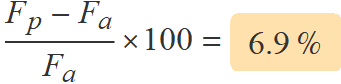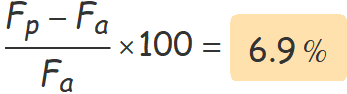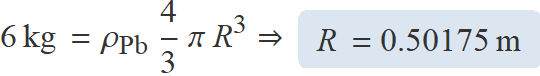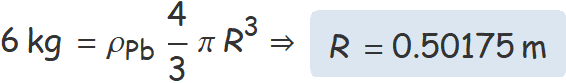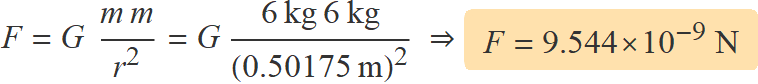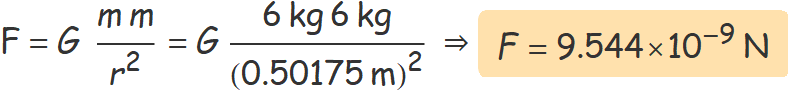Bloc E
Orbita o cau
Ho has de saber
• Entendre que les forces gravitatòries produeixen en alguns casos moviments de caiguda lliure i en altres moviments orbitals.
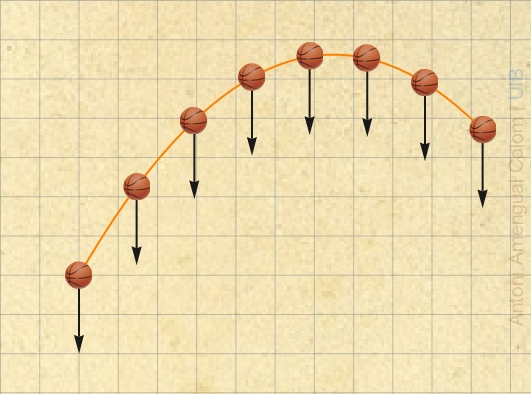
• Prop de la superfície d'un planeta o d'una lluna, la trajectòria d'un objecte llançat és parabòlica perquè l'acceleració de la gravetat es considera constant.
La teoria de la gravitació universal de Newton 
Uns 80 anys després de la formulació de les lleis del moviment planetari de Kepler, Isaac Newton va donar l'explicació de perquè els planetes orbitaven el Sol d'acord amb aquelles lleis.
En el llibre "Philosophiæ Naturalis Principia Mathematica", publicat el 1687, Newton va formular la famosa llei de la gravitació universal:
«Cada partícula de matèria de l'univers atreu cada altra partícula amb una força que és directament proporcional al producte de les masses i inversament proporcional al quadrat de la distància que les separa.»
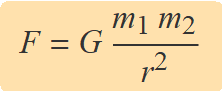
La constant de proporcionalitat és la constant de gravitació universal que es determina experimentalment i val, aproximadament,
G = 6.6743 10−11 N m2 kg−2
El Sol i els planetes eren com a esferes i quan se sumava l'atracció entre totes les seves partícules el resultat era que:
Dues esferes de masses M1 i M2 s'atreuen amb força que és directament proporcional al producte de les masses i inversament proporcional al quadrat de la distància entre els centres de les esferes.
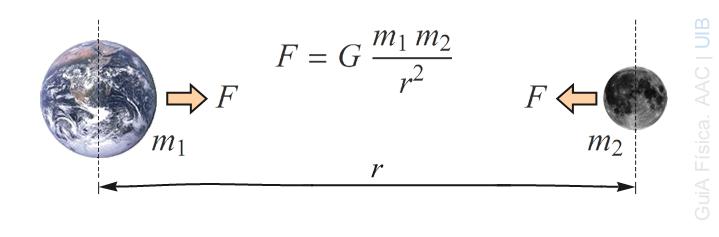
La força d'atracció gravitatòria entre dues masses puntuals és proporcional a les masses i inversament proporcional al quadrat de la distància entres elles.
Newton aplicà la llei de gravitació universal per calcular la trajectòria d'un planeta al voltant del Sol i va deduir les lleis de Kepler matemàticament.
Amb tots els èxits de la llei de la gravitació universal de Newton, cal saber que és una aproximació. Quan s'intentà aplicar la llei per calcular la trajectòria de Mercuri, es va trobar una discrepància entre la trajectòria observada i els resultats matemàtics. Es va pensar si hi havia un planeta desconegut que s'hagués de tenir en compte. Finalment, va ser clar que la llei era aproximada perquè perd validesa quan la intensitat del camp gravitatori creix (el camp gravitatori del Sol dins la zona de l'òrbita de Mercuri ja era suficientment gran per notar discrepàncies). Per a camps gravitatoris intensos s'ha d'aplicar la teoria general de la relativitat.
Prop de la superfície terrestre 
L'estudi del moviment d'objectes prop de la superficie de la Terra, la lluna o altres planetes qes realitza negligint la curvatura de l'astre uan l'abast és petit i se suposa que l'atracció gravitatoria és constant. En el cas de la Terra, mentre l'objecte no s'allunyi molt de la superfície, la distància entre el centre del planeta i l'objecte serà quasi igual al radi de la Terra. Per tant, amb
RT (radi mitjà de la Terra) = 6378 km,
MT (massa de la Terra) = 5.972 × 1024 kg.
la força d'atracció sobre un objecte de massa m és
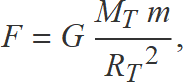
i l'acceleració
a = F / m ≈ 9.8 m/s2.
En el cas de la Lluna, també en un moviment de curt abast i prop de la superfície, es tindrà
RL (radi mitjà de la Lluna) = 1737 km,
ML (massa de la Lluna) = 7.348 × 1022 kg.
i l'acceleració de caiguda d'un objecte serà
a = F / m ≈ 1.62 m/s2.
Negligint el fregament amb l'aire, quan un objecte es llança des d'una altura h amb una velocitat v0 que forma un angle α amb l'horitzontal, les equacions del moviment són un moviment uniforme en direcció horitzontal (eix x) y un moviment uniformement accelerat en dirección vertical:
x(t) = v0 cos(α) t,
y(t) = h + v0 sin(α) t − g t2/2,
vy(t) = v0 sin(α) − a t.
La trajectoria serà vertical si l'objecte es deixa caure (v0 = 0) o parabòlica en altre cas.
La trajectòria deixa de ser parabòlica a causa de la fricció amb l'aire.
L'estudi s'amplia en el tema de la caiguda vertical d'un objecte
Lluny de la superfície. Cau o orbita? 

Exercicis resolts 
Força del Sol sobre la Terra 

La Terra segueix una trajectòria el·líptica al voltant del Sol. El periheli és el punt de l'òrbita més proper al Sol i està a 147.1 106 km de l'estrella. L'afeli és el punt més llunyà i està a 152.1 106 km.
a) Què val la força del Sol sobre la Terra quan passa per l'afeli?
b) I quan passa pel periheli?
c) En quin tant per cent augmenta la força d'atracció del Sol sobre la Terra entre el pas de la Terra per l'afeli i el pas pel periheli?
MS (massa del Sol) = 1.989 × 1030 kg,
MT (massa de la Terra) = 5.972 × 1024 kg.
Resolució mostrar
Atracció màxima entre dues esferes de plom 
Determina la força d'atracció gravitatòria màxima entre dues esferes de plom de 6 kg.
ρPb (densitat del plom) = 11.34 kg/m3,
volum esfera de radi R = 4 π R3 / 3.
Resolució mostrar


 Portada
Portada Índex temes
Índex temes