Indicaciones
para ejercicios de clase
Ejercicio: Determina el tamaño mínimo de un espejo para que puedas verte de cuerpo entero en él. ¿Determina cómo depende este tamaño de la distancia a la que te encuentres del espejo? (problema resuelto en clase)
Ejercicios 2 y 3 (página 16): Recuerda que en clase planteamos el ejercicio 2 pero no resolvimos la integral final. Asegúrate de que sabes resolverla. El ejercicio 3 lo resolvimos como comentario del ejercicio 2. Escríbe la solución explícitamente.
Ejercicio 4 (página 16): Ejercicio resuelto en clase. Comprueba que sabes resolverlo por tí solo.
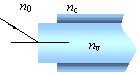
Ejercicio: Determina el dominio de los ángulos de incidencia para que el rayo de entrada quede atrapado dentro de la guía mostrada en la figura en función de los índices de refracción del vidrio en el núcleo de la guia, de la capa que lo envuelve y del medio exterior.
Ejercicio: Escribe la ecuación de la superfície de revolución que separa dos medios de índices de refracción 1 y 1.5 para que los rayos que proceden de un punto sobre el eje óptico en p=-30 cm converjan en q=40 cm. Comprueba que esta superfície no es una esfera.
Ejercicio: Demuestra matemáticamente que una superfície parabólica es la que consigue reflejar todos los rayos paralelos a su eje hacia un único punto.
Ejercicio 1 (página 43): El propósito de este ejercicio es ilustrar el mérito de un criterio de signos para unificar en una expresión casos distintos. Se puede resolver de dos maneras: i) El criterio de signos no se usa. Se llega a la expresión final y se nota que hay signos que no son los mismos que los de la expresión final derivada para otro caso. Resulta evidente que usar un criterio de signos es necesario si se quiere siempre la misma expresión final. ii) El criterio de signos se aplica desde el principio. En este caso sea cual sea el caso, se comprueba que la expresión final es siempre la misma.
En la clase de dia 5 de noviembre empecé la resolución según el modo i. No lo acabamos porqué se entendió que había dos maneras de resolver el ejercicio.
Si se quiere hacer el ejercicio según el modo ii, se puede usar el diagrama siguiente (identifica tú los ángulos). Segun este dibujo n2 es menor que n1. Igual que se pidió en clase.
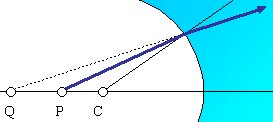
Según el criterio de signos: a y b serán positivos, mientras que qi, qk y g serán negativos.El triángulo con base PC y vértice en el punto de refracción tiene los ángulos a, qi y p+g (+ porque g ya es una cantidad negativa) de manera que su suma debe ser p. Teniendo en cuenta que el valor de qi es negativo, la suma será a - qi + p + g = p. Así pues, qi = a + g. Determinar qk no debería ser difícil.
Al dejar la clase se me ha planteado qué ocurriría si el rayo se refractara mucho y el punto Q quedase a la derecha de la superfície refringente. El nuevo diagrama sería como el siguiente:
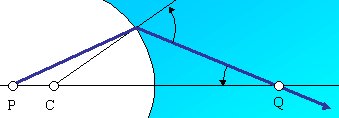
Según nuestro criterio, el único ángulo que ha cambiado el signo es beta. Ahora es el ángulo es negativo. Del triángulo con base CQ y vértice en el punto de refracción se tiene: -b +(p + qk) - g = p (recordad que qk es negativo). Por tanto qk = b + g.
Si nos ajustamos al criterio de signos, entonces siempre se tendrá: qi = a + g y qk = b + g.
Ejercicio 2 (página 44): Tienes la solución escrita.
Ejercicio: Deriva las ecuaciones (15) y (16) (página 47) a partir de (13) y (14).
Si g es pequeño, su coseno y su secante son prácticamente iguales a 1, la distancia p = R-(-p0+R)secg es aproximadamente igual a p0 y, por consiguiente, la ecuación (13) proporciona x(g) = D(p0)-R = q0-R que es la ecuación (15).
Para derivar (16) a partir de (14), seng se aproxima por la tangente y/(-p0+R); entonces y(g) = (D(p0)-R)(y/(-p0+R)). Después de sustituir D(p0) por su valor según (12), restarle R y operar, se obtiene la ecuación (16).
Ecuación de Descartes para una superficie refringente
Ejercicio: Dos medios de índices de refracción 1 y 1.5 están separados por una superficie esférica cuyo radio es, en valor absoluto, 50 cm. En las cuatro figuras inferiores se muestran cuatro problemas por resolver: El valor de p indica la posición de un objeto de altura 1 cm. Calcula la posición y la altura de su imagen y haz un dibujo esquemático colocando el objeto y la imagen con sus tamaños aproximados.
Para ver la solución de cada caso coloca el cursor sobre el cuadro de cada dibujo; aunque conviene que no la mires hasta después de haberla calculado.
La flecha azul representa el objeto y la naranja su imagen.
Ejercicio 3 (página 48): La solución es la siguiente:

Ejercicio: Una lente está limitada por dos superfícies esféricas, dibuja la sección de todas las lentes posibles según los signos de los radios de estas superfícies. Comprueba que los signos de sus distancias focales en aire indican si la lente es convergente o divergente.
Ejercicio: Considera una lente delgada convergente y después una divergente. Traza los rayos principales desde el extremo de un objeto de altura apropiada colocado a 3f, 2f, f/2, -3f, -2f i -f/2. Comprueba tu solución con la LenteD.exe.
Ejercicio 4 (página 48): Pendiente de resolución en clase
Ejercicio 5 (página 48): Pendiente de resolución en clase.
Ecuación de Descartes para una lente delgada
Ejercicio: Considera una lente convergente delgada de focal 50 cm. Calcula la posición y el tamaño de la imagen de un objeto de altura 1 cm colocado en p=-200 y en p=200 cm. A continuación, considera una lente divergente delgada de focal -50 cm y haz los mismos cálculos con el mismo objeto a -300 y a 300 cm de la lente. Utiliza el programa LenteD para comprobar los resultados.
Aplica la ecuación de Descartes y la expresión del aumento transversal para conseguir la posición y el tamaño de la imagen. En el primer caso (p=-200) el objeto está a la izquierda de la lente. Su imagen queda a la derecha de la lente y está invertida (como reflejará el signo negativo del aumento transversal).
Comentario para el ejercicio de las pupilas
Enunciado: El sistema óptico de la figura está formado por dos lentes convergentes y un diafragma en el centro. Calcula la imagen de una fuente puntual situada a 36.4 cm a la izquierda de la primera lente. Determina las pupilas de entrada y de salida del sistema.
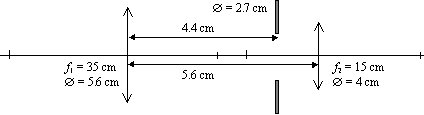
Comentario: Para determinar la pupila de entrada y de salida del sistema debemos averiguar qué diafragma o montura limita la entrada de los rayos de luz. Si no lo has hecho, convendría que leyeras el complemento sobre diafragmas y pupilas. Las trayectorias de los rayos procedentes de un punto sobre el eje a 36.4 cm de la primera lente son como las del diagrama de la derecha (no deberías tener ningún problema para obtener uno equivalente con el programa soc). Resulta obvio que el diafragma es lo que limita la entrada de los rayos de luz y por tanto es el diafragma de apertura. La pupila de entrada será su imagen por la lente de la izquierda y la pupila de salida la generada por la lente de la derecha.

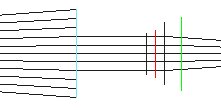
Mirando hacia la entrada, veríamos un círculo dentro de la montura de la primera lente delimitado por el diafragma. Matemáticamente esto se justifica calculando los ángulos que forma el eje óptico con las líneas que unen el punto del eje base del objeto y los extremos de las imágenes de L1, el diafragma (arctan( (3.09/2)/(5.03+36.4)) = 2.13º) y L2 (3.12º). El ángulo más pequeño es el de la imagen del diafragma y, por tanto, éste actúa como diafragma de apertura. La pupila de entrada será su imagen por L1, que ya hemos calculado, y la pupila de salida será la imagen del diafragma por L2 (su diámetro es 2.93 y está a 1.30 cm de la segunda lente entre ella y el diafragma).
ÓPTICA. Antoni Amengual. Departament de Física, Universitat de les Illes Balears



