Ángulo sólido y estereoradianes

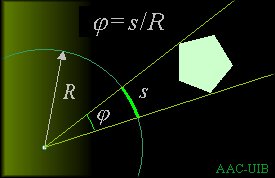
Considérese un objeto plano (en la figura inferior se trata de un pentágono) y un punto P de referencia en el plano definido por el objeto. Si desde P se trazan dos rectas que tocan el perímetro del objeto sin entrar nunca en su interior ¿cúal es el ángulo formado por las dos rectas?

Una manera de contestar a la pregunta es dibujar una circunferencia centrada en el punto y medir la longitud s del arco limitado por las dos rectas. Luego, una sencilla regla de tres (s es al angulo j lo que 2pR es al ángulo 2p) permite obtener j como el cociente entre s y R.

Un problema semejante se puede enunciar con un objeto tridimensional. Ahora se debe generar un cono (de sección probablemente irregular) de manera que las rectas que surgen del punto tocan el objeto sin entrar nunca en su interior. Consideremos un ejemplo dónde el objeto se ha dibujado usando una fotografia de la NASA.

Siguiendo operaciones semejantes a las del caso unidimensional, si se dibuja una esfera de radio R alrededor del punto, las rectas que tocan el objecto, interceptan la esfera en una curva cerrada que define un sector esférico. Si el área de este sector es a, El ángulo sólido w definido por el objecto desde el punto de referencia es igual el cociente indicado en la figura. Las unidades de w son estereoradianes y su valor está entre 0 y 4p.