En la presentación de este problema en el libro se toma como un hecho que la posición de equilibrio “se da cuando la elongación del muelle multiplicada por su constante elástica es igual a (2M + m)g”. Este resultado es de hecho irrelevante para hallar la frecuencia de las oscilaciones de pequeña amplitud alrededor de la posición de equilibrio; aunque, habiéndolo mencionado, ¿cómo se determina esa igualdad? Veamos dos maneras:

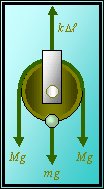
Primera: consideremos las fuerzas que actúan sobre la polea. En la figura adjunta se muestran éstas fuerzas: La que ejerce el muelle hacia arriba (igual a su constante elástica por su elongación); la que ejerce la masa en el perímetro de la polea (mg hacia abajo); y las dos fuerzas de tensión de la cuerda (en el equilibrio también hacia abajo e iguales al peso Mg; nótese que en el equilibrio, tener la cuerda con un extremo atado al suelo es equivalente a tener una cuerda con masas iguales colgadas de sus extremos). El equilibrio de las fuerzas implica, como se quería mostrar, que la elongación debe ser (2M + m)g/k. (Recuérdese que se supone que la masa de la polea es despreciable).

Segunda: consideremos que no fuéramos capaces de establecer inicialmente la elongación del muelle en el equilibrio. En este caso, al definir la energía potencial elástica escribiríamos k(z-d)2/2; dejando la variable d como una cantidad desconocida. En el libro, se escribe directamente d = (2M + m)g; de manera que al linealizar la ecuación de Euler-Lagrange se obtiene una ecuación del tipo

(1)    d²z/dt² = -w²z,

que es formalmente igual a la de un oscilador armónico. Si no se especificara valor alguno para d, al repetir el cálculo de la ecuación de Euler-Lagrange, se obtendría una ecuación del tipo

(2)    d²z/dt² = cte -w² z.

La constante que aparece en esta ecuación es una expresión proporcional a -kd + mg + 2Mg, que se anula si d es igual a la expresión dada antes y que queríamos mostrar. La situación en este problema no es nueva. La ecuación del movimiento de una masa en un plano horizontal sin fricción sujeta por un muelle de constante elástica k y longitud natural nula es una ecuación de la forma (1); y la ecuación del mismo sistema colocado verticalmente es una ecuación de la forma (2). En este segundo caso, si se cambia la coordenada original por una que mida el desplazamiento respecto a la posición de equilibrio, o si se modifica la longitud natural del muelle sin modificar su constante elástica, la ecuación toma la forma (1).

Nota: Al escribir la definición de zm[t_] copiándola del Mathematica se introdujo una errata en la página 29 del libro; pues zm[t_] aparece igual a zmeq + 2 z[t] + ... y sobra el 2. Lo correcto es zm[t_]:= zmeq + z[t] + R(...

SISTEMAS MECÁNICOS. Antoni Amengual. Departament de Física, Universitat de les Illes Balears ISBN: 84-7632-641-6