La Sección 1.2 (Un problema importante) acaba en la página 10 diciendo que un ejercicio interesante es comparar la duración del trayecto a lo largo de una línea recta, una parábola y una cicloide. Aquí se presentan algunos detalles de los cálculos y resultados numéricos.

Como en el libro, consideraremos que la partícula se mueve en el plano vertical x-z con el eje z positivo hacia arriba y que desliza desde el origen hasta el punto (x_f , -z_f).

A lo largo de una línea recta

Sea a el ángulo que forma la línea recta con el eje x, positivo en sentido horario. La ecuación de la recta será z(x)=-(z_f /x_f )x o bien z(x)=-(tana) x. El problema se puede resolver cinemáticamente: La aceleración de la partícula es g sina y el espacio que debe recorrer x_f seca. Sustituyendo en la expresión espacio = aceleracion t² / 2 se puede despejar el tiempo que se busca. Alternativamente, se puede evaluar la integral (2) del libro. La integración es trivial y si se usa la expresión z(x)=-(tana)x se consigue la solución escrita en la misma forma que con el método cinemático. Algunos resultados numéricos se ofrecerán al final.

A lo largo de una parábola

El tiempo de viaje se calcula con la integral (3) del libro (pág. 5) y el resultado es la expresión (5) (en el libro hay una errata porque falta un signo menos delante del cociente que multiplica a toda la expresión de la derecha). Como se sugiere en el libro, para llegar a la expresión (5) se puede usar el Mathematica para resolver la integral elíptica; pero conviene que los límites de integración se analicen a parte. Al hacer las operaciones, hay que tener en cuenta que el valor de a es siempre positivo (la parábola tiene los brazos hacia arriba) y que el valor de b es siempre negativo (se ve directamente de su definición). Teniendo esto en cuenta, se pueden simplificar varios términos. Por ejemplo, (a²/b²)^1/2 será a/(-b). Además, hay que usar la propiedad E(-j | x) = -E(j | x) (propiedad que se ve también directamente de la definición (4)).

A lo largo de la cicloide

Tal como se define en el libro, el valor de la constante a de la cicloide es negativo. Su valor se puede obtener con el Mathematica en dos etapas. En la primera, se dividen las expresiones de z[q]:=a(1-cosq) y de x[q]:=-a(q-sinq) para q = q_max y el cociente se iguala a -z_f / x_f para conseguir una ecuación cuya solución es q_max:

En la segunda etapa, el valor de a se obtiene a partir de x(q_max). A continuación se puede proceder ya a calcular el tiempo invertido en recorrer la trayectoria cicloidal.

Consideremos la expresión (2) como punto de partida para recuperar el resultado presentado en muchos libros de Mecánica y cuya simplicidad es notable:

El tiempo de recorrido a lo largo de la cicloide es (|a|/g)^1/2q_max.

Puesto que se tiene la forma paramétrica de la curva, la integral (2) conviene realizarla en función del parámetro q. Para ello debemos evaluar, dx y z' en función de q. Tendremos:

Al calcular estas derivadas y sustituir en (2) se comprobará que todos los términos se simplifican y queda el resultado tan simple ya indicado. (Nota: Algunos estudiantes no consiguieron ese resultado porque intentaron aplicar directamente la expresión (12) sin analizarla y como si estuviera escrita en formato de Mathematica. La expresión indica que la integral se debe realizar calculando todos los términos en función de q. El problema surge al interpretar qué es z'(q). La respuesta correcta es que z'(q) es la derivada de z respecto a x expresada en función de q. Una interpretación errónea surge al leer z'(q) directamente en notación del Mathematica e identificarla con z'[q], es decir la derivada de z respecto a q. En cualquier caso, dado que se ha producido una confusión es obvio que la notación usada debería haber sido otra.)

Comparación de los tiempos

En la siguiente figura se muestra la parábola más rápida y la cicloide que unen el origen y el punto (4, -1) (las unidades de distancia son metros). ¿Adivinas cúal es la parábola?

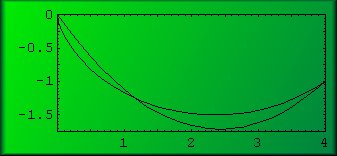
(es la que casi llega a tocar el eje de abscisas). A medida que el punto se aleja hacia la derecha, el tiempo de viaje siguiendo una cicloide es mucho menor que siguiendo una línea recta. No obstante, seguir la cicloide no supone un avance tan notorio cuando se compara con el camino parabólico más rápido. En la siguiente tabla se ofrecen los valores de los parámetros que definen la parábola más rápida y la cicloide, los tiempos de trayecto y su comparación:

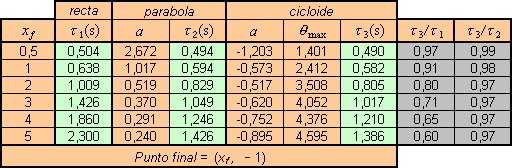
(El valor de g utilizado es 9.83 m/s²)