Sobre la obtención de la ecuación de Kepler M = E - e sinE
En un campo central newtoniano la órbita de una partícula de masas m moviéndose con energía total negativa es elíptica y, en coordenadas polares con origen en el centro de fuerzas, se tiene
r(j) = p / (1 + e cosj)
La ecuación de Kepler se usa para determinar la posición de la partícula en su órbita en función del tiempo. Este es el tipo de cálculo que se debe realizar para fijar aproximadamente la posición de un planeta alrededor del Sol. En los tres pasos siguientes se demuestra esta ecuación tomando el origen de tiempo cuando la partícula pasa por el pericentro.
El área de la órbita elíptica se puede calcular de dos maneras:
i) geométricamente: Si los semiejes mayor y menor son a
y b,
Área = pab
ii) aplicando la ley de las áreas: Si J y t
son el momento angular y el período de la órbita,
Área = (J/2m)t
Igualando las dos áreas resulta: (J/2m)=pab/t
Dado que la velocidad areolar es constante, el área barrida por el radio vector de posición desde el origen del tiempo hasta un tiempo t dado será (J/2m)t o, haciendo uso del resultado del paso anterior: pabt/t. Esta área se muestra en la siguiente figura:
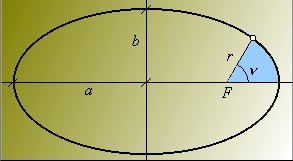
Para conocer la posición de la partícula en t se
debe determinar el valor de n para el cual
el área azul es igual a pabt/t.
Esta determinación se realiza en el tercer paso.
Si el área entre x1 y x2 de una función g(x) es A, él área entre x1 y x2 de f(x) = a g(x) será aA (a es una constante). Comprobado este hecho, consideremos la siguiente figura en la que se ha trazado una circunferencia de radio a sobre la órbita elíptica:

La gráfica de g(x) podría ser la línea desde el foco F a la posición de la partícula sobre la elipse, y desde esta posición al pericentro. Su área está indicada en azul claro y es la que se debe determinar según el paso anterior. Ahora bien, la función f(x)=(b/a)g(x) es el arco de circunferencia y por lo dicho, tendremos que:
pabt/t = área azul claro = (b/a) área azul
Pero el área en azul se puede calcular trivialmente en función
del ángulo excéntrico E como se muestra gráficamente
en la siguiente figura. El área del sector circular es la mitad
del ángulo por el radio al cuadrado y el área del triángulo
es base por altura dividido por dos. La base es igual a la distancia
del centro de la elipse al foco: ae y la altura es igual a asenE.
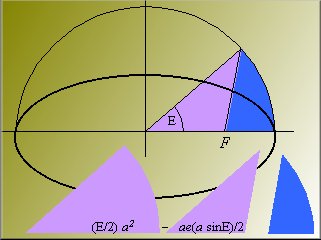
En consecuencia:
pabt/t = área azul claro = (b/a) área azul = (b/a){(E/2)a2- (ea2/2)senE}
La ecuación de Kepler se obtiene finalmente después de
simplificar términos y definir: M
= 2pt/t
M = E - e senE .
SISTEMAS MECÁNICOS. Antoni
Amengual. Departament
de Física, Universitat de les Illes Balears
ISBN: 84-7632-641-6