Temes 
Portada 
Olimpíada Equació de les ones harmòniques
Problemes 
La llum és una ona electromagnètica i el so una ona de pressió. L'estudi de les propietats matemàtiques de les ones és necessari per treballar en diversos camps de la Física.
• Escriure i interpretar l’expressió matemàtica d’una ona harmònica transversal
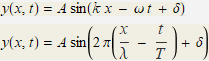
• Que el sinus es pot canviar per cosinus restant π/2 a la fase δ.
• El significat de longitud d'ona λ, nombre d'ones k, període T, freqüència angular ω i fase δ.
• Determinar la velocitat de propagació de l'ona
• Determinar l'equació de la vibració i la velocitat de les partícules que formen una ona material
1
Les equacions de cinc ones harmòniques són:
y(x, t) = 24 sin(3 x − 5 t),
y(x, t) = 17 cos(2 x − 4 t),
y(x, t) = 36 cos(−x − 7 t),
y(x, t) = 19 cos(−5 x + t),
y(x, t) = 45 sin(−6 x + 5 t),
on x s'ha d'expressar en metres, t en segons i y en les unitats pròpies d'una pertorbació qualsevol, quina és l'amplitud de l'ona d'aquest llistat que es desplaça cap a l'esquerra?
1) L'ona harmònica 
2) L'ona harmònica
2
Les equacions de sis ones harmòniques són:
y(x, t) = 20 cos(2 x − 2 t),
y(x, t) = 15 cos(4 x + 2 t),
y(x, t) = 18 cos(8x − 4 t),
y(x, t) = 27 cos(2 x − 4 t),
y(x, t) = 32 cos(4 x + 8 t),
y(x, t) = 25 cos(8 x − 4 t),
on x s'ha d'expressar en metres, t en segons i y en les unitats pròpies d'una pertorbació qualsevol, quina és l'amplitud de l'ona d'aquest llistat que es desplaça a 2 m/s cap a la dreta?
3
Per a l'ona harmònica y(x, t) = 18 cos(2π (x/7.5) − 2 t),on x s'ha d'expressar en metres, t en segons i y en cm, quina és l'amplitud de la pertorbació a x = 22.5 m quan l'amplitud és màxima a x = 0?
4
En un canal rectangular llarg es genera una ona harmònica a la superfície de l'aigua. L'altura de la superfície de l'aigua en una regió del canal es calcula amb l'equació d'una ona harmònica d'amplitud 2 cm. La longitud d'ona és 15 cm i l'ona es propaga a 0.29 m/s, on x s'ha d'expressar en metres, t en segons i y en cm. L'animació següent representa un tall en la direcció x d'aquesta ona.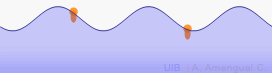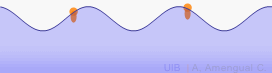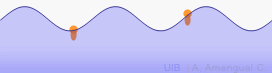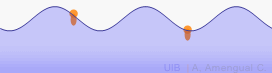 
Quina és l'altura de la superfície de l'aigua a x = 50 cm i t = 4.9 s si en aquesta posició l'altura ha estat màxima a t = 4.5 s?
5
Què ha de valer la fase δ de l'ona harmònica que es desplaça cap a la dreta d'amplitud 15 cm, nombre d'ones 4.7 m-1 i freqüència angular 2.1 rad/s, perquè la pertorbació a l'origen valgui zero a l'instant t = 7 s?
Atenció: La fase que s'ha d'escriure dins el requadre per comprovar la resposta és un angle del primer quadrant.
6
Què ha de valer el nombre d'ona de l'ona harmònica que es desplaça cap a la dreta
y(x, t) = 16 sin(k x − 1.2 t + 45º)
on x s'ha d'expressar en metres, t en segons i y en les unitats pròpies de la pertorbació que es vulgui tractar, perquè aquesta pertorbació a x = 0.8 m sigui màxima a l'instant t = 4 s i el nombre d'ona sigui el més petit possible?
7
L'equació d'una ona mecànica transversal és
y(x, t) = 9 sin(5 x − 3 t),
on x s'ha d'expressar en metres, t en segons i y en centímetres, quina és la velocitat de propagació de l'ona?
8
Per a l'ona harmònica de l'exercici anterior, quina és la velocitat màxima de vibració de les partícules que la formen?
9
L'equació d'una ona mecànica transversal és
y(x, t) = 7 cos(k x − 4 (rad/s) t),
on x s'ha d'expressar en metres, t en segons i y en cm. Què ha de valer el nombre d'ona perquè la velocitat de propagació sigui el triple que la velocitat de vibració màxima de les partícules que formen l'ona?
10
L'equació d'una ona mecànica transversal és
y(x, t) = 5 cos(3 x − ω t),
on x s'ha d'expressar en metres, t en segons i y en cm. Què val ω si la pertorbació es propaga a 2.7 m/s?
