Camp magnètic
Força de Lorentz
- 1. Exercicis resolts
- 1.1. Direcció i sentit de la força usant la mà dreta
- 1.2. Trajectòries de tres partícules
- 1.3. Dues trajectòries circulars
- 1.4. Partícula que perd una fracció de la massa
- 1.5. Nombre de voltes completades per un protó
- 1.6. Una component de la força de Lorentz
- 2. Exercicis per resoldre
- 2.1. Enunciats

La força de Lorentz 
S'anomena força de Lorentz a la força que actua sobre una partícula amb càrrega elèctrica quan és mou dins un camp magnètic.
L'expressió que dona la força de Lorentz és la següent (es troba en el formulari)
F = q v × B
q = càrrega de la partícula,
v = velocitat de la partícula,
B = camp magnètic.
El mòdul de la força de Lorentz és
F = q v B sin(α)
on α és l'angle que formen el vector velocitat i el vector camp magnètic.
Quan la velocitat i el camp magnètic són perpendiculars, α = 90° i
F = q v B.
Quan la velocitat i el camp magnètic tenen la mateixa direcció, α = 0° o α = 180°,
F = 0.
La direcció de la força de Lorentz és perpendicular a la velocitat i al camp magnètic.
El sentit de la força és pot determinar amb la mà dreta posant els dits com mostra la figura. El dit índex, el dit del mig i el polze de la mà dreta es col·loquen formant angles rectes entre ells, com els eixos de coordenades x, y i z.

El dit índex es posa en la direcció de la velocitat.
El dit del mig es posa en la direcció del camp magnètic.
El dit polze indica la direcció i el sentit de v × B.
La força de Lorentz té el sentit de v × B si la càrrega de la partícula és positiva, i sentit contrari si la càrrega és negativa.
Representació d'un camp uniforme 
Un camp magnètic igual en tots els punts d'una regió es diu que és uniforme.
S'usen aquí dos tipus de gràfics per representar un camp uniforme en un pla:

La repetició del símbol ⊗ representa un camp uniforme cap a dins del pla del dibuix.

La repetició del símbol ⊙ representa un camp uniforme cap a fora del pla del dibuix.
Trajectòries 
La trajectòria d'una partícula amb càrrega elèctrica dins un camp magnètic uniforme és:
recta si la velocitat és paral·lela al camp;
circular si la velocitat és perpendicular al camp
helicoidal en altre cas.
En aquest curs es consideren les trajectòries circulars i la resolució de problemes per determinar una propietat de la partícula (massa, càrrega o velocitat), del camp magnètic (sentit o intensitat) o la trajectòria (radi, període i sentit del gir).
Quan la velocitat inicial és perpendicular al camp, la força de Lorentz serà constant i perpendicular a la velocitat i això genera una trajectòria circular continguda en un pla perpendicular al camp.
Igualant l'expressió de la força centrípeta a la força de Lorentz, s'obté


Igualant la velocitat a la longitud d'una trajectòria circular de radi R dividida pel període per completar-la, s'obté


Aquestes dues equacions són les necessàries per resoldre els problemes.
La força de Lorentz és una força centrípeta que corba la trajectòria de la partícula carregada. La força apunta cap al centre de l'arc circular.
Per determinar si una partícula amb càrrega negativa seguirá un arc circular movent-se en sentit horari o antihorari, fes el següent:
• Posa la mà dreta amb el dit polze apuntant en la direcció i el sentit del camp magnètic, i la resta de dits apuntant en la direcció de la velocitat de la partícula.
• Doblega un poc els dits de la mà mantenint el polze en la direcció del camp.
• Mira els dits doblegats. Aquests dits indiquen si la partícula es mourà en sentit horari o sentit antihorari sobre la circumferència.
Si es coneix com es mou una partícula i els dits doblegats indiquen el sentit observat, la partícula té càrrega negativa, si no, té càrrega positiva.

Exercicis resolts 
Direcció i sentit de la força usant la mà dreta 
Dues partícules amb càrrega elèctrica entren dins un camp magnètic uniforme amb la mateixa velocitat inicial perpendicular al camp. Les trajectòries s'han representat a la figura següent. S'ha dibuixat el vector velocitat en el punt a i el vector producte v × B.

a) Orienta el dit índex paral·lel a la velocitat i el dit mig, paral·lel al camp magnètic. Verifica que el dit polze marca v × B.
b) Quin signe té la càrrega de la partícula en el punt a?
c) Dibuixa el sentit de la força sobre la partícula en el punt b i determina el signe d'aquesta partícula?
Resolució mostrar
a) Verificació del sentit de v × B 

b) Signe de la càrrega de la partícula en el punt a 
El centre de la circumferència que segueix la partícula a està a la part interior de la curva. La força de Lorentz apunta en aquest sentit que és el mateix que el de v × B. Per tant, q > 0. La partícula té càrrega positiva.
c) Signe de la càrrega de la partícula en el punt b 
Si la partícula que passa pel punt a s'ha desviat cap a l'esquerra i té càrrega negativa, la partícula que s'ha desviat cap a la dreta ha de tenir signe contrari. La partícula que passa pel punt b té càrrega negativa.
O amb el índex paral·lel al vector velocitat en el punt b i el dit del mig cap a baix, el dit polze indica cap a l'exterior de la corba. Per tant, el signe de q ha de ser negatiu perquè q v × B indiqui cap a l'interior.
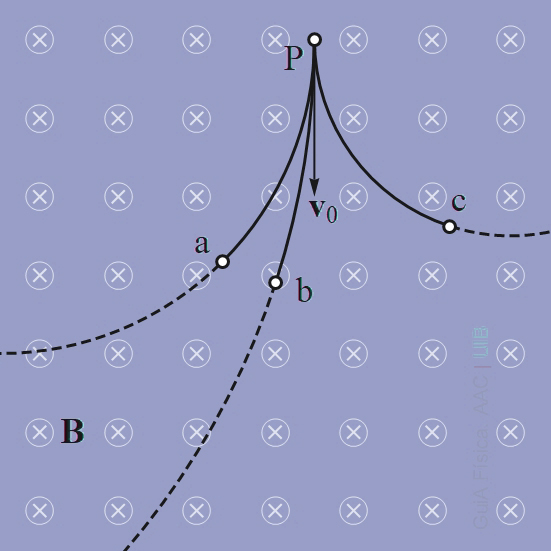
ocultarTrajectòries de tres partícules 
Tres partícules de la mateixa massa tenen càrregues elèctriques. Per determinar el signes de les càrregues, les partícules s'injecten amb la mateixa velocitat v0 dins una regió on hi ha un camp magnètic uniforme perpendicular a la velocitat. Es registre la trajectòria de les partícules, la qual es reprodueix a la figura.
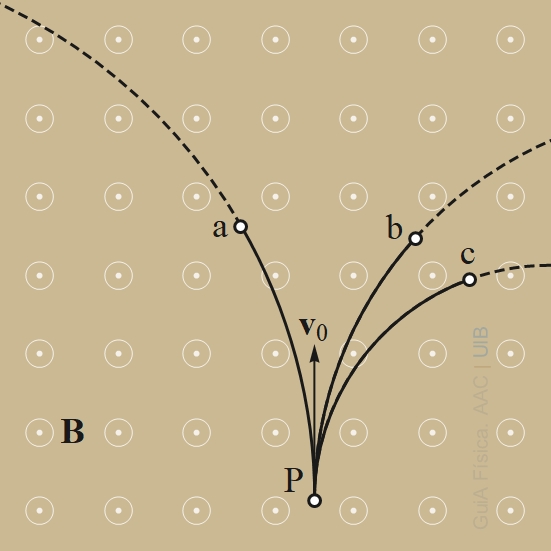
a) Quin tipus de corba és la trajectòria de les partícules?
b) Quins signes tenen les càrregues de les partícules?
Resolució mostrar
a) Tipus de corba 
La trajectòria d'una partícula dins un camp magnètic uniforme quan la velocitat inicial és perpendicular al camp és una circumferència. Per tant les corbes de la figura són arcs de circumferències.
b) Signes de les càrregues 

El sentit cap a on es devia una partícula carregada es pot determinar amb la regla amb la mà dreta. La mà dreta es posa de manera que el dit polze marqui el sentit del camp magnètic. Els altres dits un poc doblegats marquen la curvatura de la trajectòria d'una partícula amb càrrega negativa.
Les partícules que tenen la trajectòria corbada al revés tenen càrrega positiva. Així:
qa < 0 qb > 0 qc > 0
Alternativament, el signe de la càrrega de cada partícula es pot determinar amb el sentit de la força de Lorentz:
Inicialment, el producte vectorial v0 × B dona una vector cap a la dreta. La força de Lorentz va en aquest sentit si q > 0 i, cap a la dreta, si q < 0. El sentit de la força en el moment inicial, determina en quin sentit es desvia la partícula:
Amb càrrega positiva, la partícula es desvia cap a l'dreta.
Amb càrrega negativa, la partícula es desvia cap a l'esquerra.
ocultarDues trajectòries circulars 
Les partícules carregades dins un camp magnètic uniforme perpendicular a la velocitat de les partícules segueixen una trajectòria circular. El motiu és que la força de Lorentz és una força perpendicular a la velocitat i actua com a una força centrípeta constant sobre les partícules.
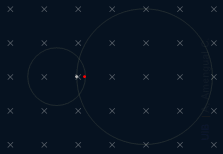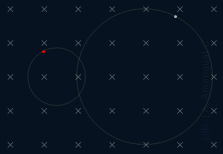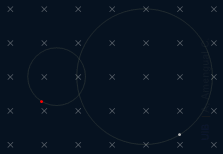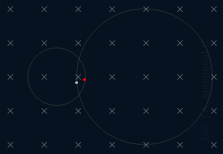
Les dues partícules representades a la figura tenen la mateixa relació càrrega/massa en valor absolut,


a) Sigui v1 la velocitat de la partícula vermella de la trajectòria esquerra i T1 el temps que tarda en completar una volta. Sigui v2 la velocitat de la partícula blanca de la trajectòria dreta i T2 el seu període. Calcula T2/T1.
b) Si només es veíes la trajectòria circular no es podria saber el signe de les càrregues, però veient com es mouen, sí. Quin signes tenen les càrregues q1 i q2 de les dues partícules?
c) Determina el mòdul de la força magnètica sobre una partícula de 3.6 10−12 kg amb una càrrega elèctrica de −5.0 μC quan es mou a 350 km/s dins un camp magnètic de 0.3 T.
d) Determina el diàmetre de la trajectòria de la partícula de l'apartat c.
Resolució mostrar
a) Relació entre els períodes 
La força de Lorentz és la força centrípeta que corba la trajectòria de la partícula, llavors, igualant la força centrípeta al mòdul de la força de Lorentz quan la velocitat i el camp són perpendiculars es té


El període (temps per completar una volta) és igual a la longitud de la circumferència dividida per la velocitat,


Si les partícules tenen la mateixa relació carrega/massa en valor absolut, el període és el mateix. Encara que no tenguin la mateixa velocitat, completen una volta en el mateix temps perquè, si una partícula es mou amb una velocitat més gran, també és proporcionalment més gran el radi de la circumferència que segueix. Per tant,


b) Signes de les càrregues 

La mà dreta es posa per damunt del dibuix amb el dit polze marcant cap a dins, que és el sentit del camp magnètic.
Es altres dits marquen la curvatura de la trajectòria de la partícula blanca.
Llavors; la partícula blanca té càrrega negativa i la vermella càrrega positiva.
c) Força magnètica 
La força magnètic no depèn de la massa de la partícula.
|F| = |q| v B = 0.525 N
d) Diàmetre de la trajectòria 
Partícula que perd una fracció de la massa 
Una partícula de 2 μg carregada elèctricament segueix una trajectòria circular de 0.52 m de radi dins un camp magnètic uniforme perpendicular a la velocitat incial.
Determina quin serà el radi de la nova trajectòria circular si la partícula perd la meitat de la càrrega elèctrica.
Nombre de voltes completades per un protó 
Calcula quantes voltes completa un protó a 320 km/s durant 2 μs dins un camp magnètic de 0.2 T perpendicular a la velocitat?
Una component de la força de Lorentz 
Una partícula de 4 μg carregada amb 50 μC es mou dins un camp magnètic. El camp magnètic és uniforme de 3.7 T en la direcció de l'eix z. Aquest camp magnètic és molt intents. Què val la component en direcció x de la força magnètica sobre la partícula quan passa per l'origen de coordenades si en aquest moment vx = 210 km/s i vy = 520 km/s?
Exercicis per resoldre 

La força sobre una càrrega elèctrica en moviment dins un camp magnètic s'anomena força de Lorentz pel físic Hendrik Lorentz.
Enunciats 
1
Tres partícules de la mateixa massa tenen càrregues elèctriques diferents. Les partícules s'injecten amb la mateixa velocitat v0 dins una regió on hi ha un camp magnètic uniforme, perpendicular a la velocitat, per determinar els signes de les càrregues.

Les trajectòries registrades de les partícules es reprodueixen a la figura.
a) La corba seguida per les partícules és circular o parabòlica?
b) Quins signes tenen les càrregues de les partícules?
2
Tres partícules de la mateixa massa tenen càrregues elèctriques diferents. Les partícules s'injecten amb la mateixa velocitat v0 dins una regió on hi ha un camp magnètic uniforme, perpendicular a la velocitat, per determinar els signes de les càrregues.

Les trajectòries registrades de les partícules es reprodueixen a la figura. Determina els signes de les càrregues de les partícules.
"Regla de la mà esquerra"
Posa la mà esquerra de manera que el dit polze apunti en la direcció i el sentit del camp magnètic i que la resta de dits apuntin en la direcció de la velocitat de la partícula.
Doblega un poc els dits de la mà mantenint el polze en la direcció del camp.
La curva que fa la mà esquerra indica la curvatura de la trajectòria d'una partícula amb càrrega positiva.
3
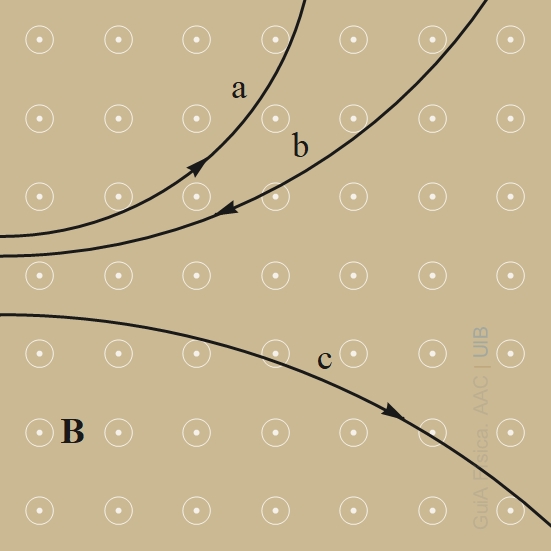
Usa la regla de la mà dreta per determinar els signes de les càrregues de les partícules a partir de les trajectòries representades a la figura.
4
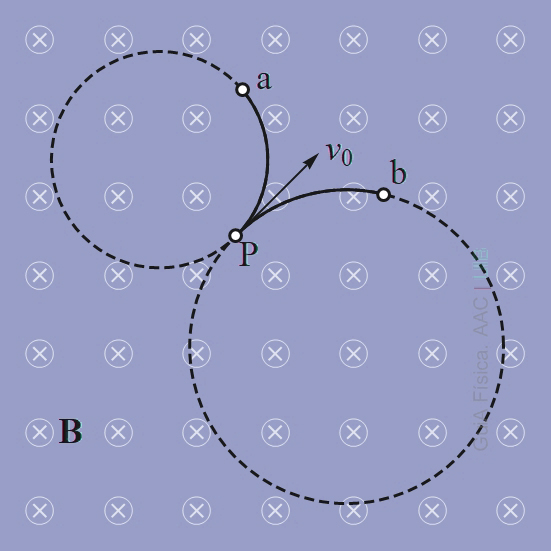
Usa la regla de la mà dreta per determinar els signes de les càrregues de les partícules a partir de les trajectòries representades a la figura..
5
Tres partícules, identificades com a, b i c, tenen una massa de 2 μg i segueixen les trajectòries representades a la figura de l'exercici número 2, que es torna reproduir aquí. Les tres partícules passen pel punt P amb la mateixa velocitat v0 = 3 km/s. la intensitat del camp magnètic uniforme és d'1.5 T.

a) Calcula el valor absolut de la càrrega elèctrica en microcoulombs de la partícula identificada amb la lletra a si la seva trajectòria té 64 cm de radi.
b) Quina partícula segueix la trajectòria circular amb el radi més gran?
c) Quina partícula té la càrrega elèctrica més gran en valor absolut?
d) Quin és el signe de la càrrega elèctrica de cada partícula?
e) Quantes voltes completa la partícula c durant 120 ms dins el camp magnètic uniforme si la seva càrrega elèctrica en valor absolut és de 0.75 μC.
6
Dues partícules de 7 μg, identificades com a i b, segueixen les trajectòries representades a la figura, dins un camp magnètic uniforme B de 0.35 T. Les dues partícules passen per un punt P amb la mateixa velocitat v0 = 6 km/s.
a) Calcula el valor absolut de la càrrega elèctrica en mC de la partícula b si la seva trajectòria té 60 cm de radi.
b) Quina partícula té la càrrega elèctrica més petita en valor absolut?
c) Quin és el signe de la càrrega elèctrica de cada partícula?
c) Calcula el temps en segons que tarda la partícula a, que té una càrrega elèctrica de 2.9 μC en valor absolut, en completar 240 voltes.
7
El ciclotró va ser desenvolupat per Ernest O. Lawrence i M. Stanley Livingstone a principis de la dècada de 1930.

En el ciclotró, es crea un camp magnètic uniforme intens perquè partícules carregades elèctricament segueixin una trajectòria circular. Com que la força de Lorentz no augmenta la velocitat de la partícula, el dispositiu té una zona estreta dins el camp magnètic on també hi ha un camp elèctric el qual accelera la partícula carregada quan l'atravessa.
A la sortida del camp elèctric, la partícula només està sotmesa a la força de Lorentz i segueix una trajectòria semicircular. Al completar aquesta mitja volta, la partícula entra de nou a la zona de camp elèctric, el qual s'ha invertit, per accelerar (i no frenar) la partícula. Així, la partícula guanya velocitat cada vegada que travessa per la zona de camp elèctric el sentit del qual s'inverteix perquè sempre acceleri la partícula. La presència del camp magnètic serveix perquè la partícula faci voltes i creui la zona de camp elèctric i guanyi velocitat repetidament.
a) El dispositiu funciona perquè el temps Tm que tarda una partícula carregada en completar mitja volta dins el camp magnètic uniforme no depèn de la velocitat i se sap quan s'ha d'haver invertit el sentit del camp elèctric. Dedueix l'expressió que dona Tm a partir de l'acceleració centrípeta i el mòdul de la força de Lorentz. Quina de les expressions següents correspon a Tm:




b) El doble de Tm és el temps que tarda una partícula en completar una volta. La freqüència angular ω = 2π/T es denomina freqüència angular de ciclotró de les partícules. Calcula la freqüència de ciclotró de partícules alfa.
Massa partícula α = 6.64 × 10−27 kg,
Càrrega partícula α = 3.20 × 10−19 C.
8
Ernest O. Lawrence, coinventor del ciclotró, ja va usar un ciclotró de 152 cm de diámetre per accelerar protons que, amb col·lisions amb àtoms, creaven isòtops radioactius de fósfor-32 amb els que tractar pacients de leucèmia. Actualment, el protons també s'usen directament amb el tractament del càncer en l'anomenada teràpia de protons. L'avantatge d'aquesta teràpia és que els feix de protons es pot concentrar millor sobre el tumor sense afectar els teixits sans del voltant. El protons s'acceleren amb un ciclotró i amb alta energia es dirigeixen al tumor per eliminar les cèl·lules cancerígenes.
a) Calcula la freqüència de ciclotró ωc de protons dins un camp magnètic de 0.95 T.
b) En una màquina de teràpia de protons, la velocitat dels protons arriba al 60 % de la velocitat de la llum. Calcula la distància recorreguda en línia recta per un protó amb aquesta velocitat en el temps 2π/ωc?
c) D'acord amb el resultat de l'apartat anterior, es podria usar un accelerador lineal per assolir la mateixa velocitat dels protons dins una sala hospitalària de mida normal? Respon, sí o no.
Massa protó = 1.673 × 10−27 kg,
Càrrega protó = 1.6022 × 10−19 C.
9
Una partícula de 2 mg amb una càrrega elèctrica de 2 mC en valor absolut segueix una trajectòria circular de 65 cm de radi, dins un camp magnètic uniforme de 0.6 T perpendicular al pla de la trajectòria. Els símbols ⊙ indiquen el sentit del camp i les fletxes sobre la circumferència, el sentit del moviment de la partícula. Determinau, justificant cada resposta:

a) El signe de la càrrega de la partícula.
b) La velocitat de la partícula en km/s.
c) El mòdul de la força magnètica sobre la partícula en newtons.
d) Quantes voltes completa la partícula durant 1 s.
10
En una regió on el camp magnètic es constant es pot injectar una partícula amb una velocitat controlada a través d'un forat H. Es tenen dos tipus de partícules. Tenen la mateixa massa m però càrregues q1 i q2 diferentes.
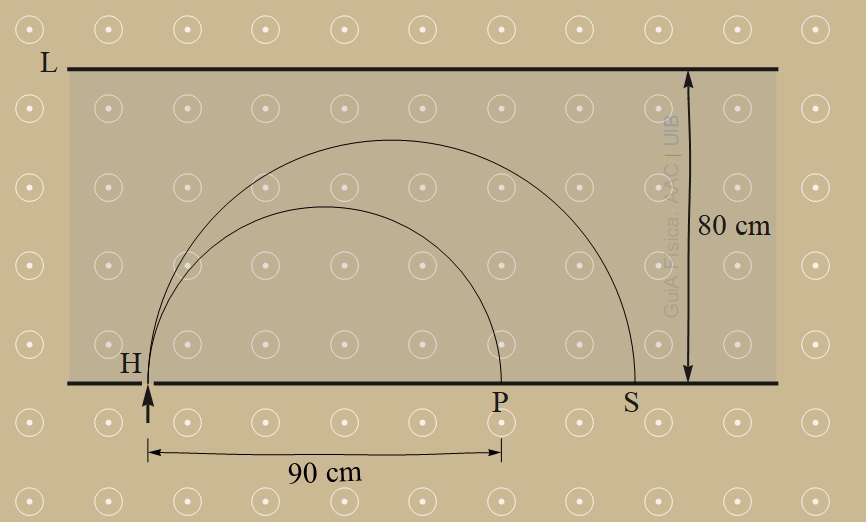
a) Per aconseguir que una partícula de càrrega q1 injectada a v0 = 2 km/s impacti en el punt P, a 90 cm del punt d'injecció H, el camp magnètic s'ha d'ajustar a 0.18 T. Determina el quocient q1/m en C/kg.
b) Una partícula de càrrega q2 impacta en el punt S, a 124 cm de l'entrada H quan s'injecta amb la mateixa velocitat v0 anterior. A partir de l'expressió de q/m en funció de la velocitat, la intensitat del camp i el radi de la trajectòria, argumenta si q2 és més gran o més petit que q1. És q2 més gran que q1?
c) Determina la velocitat màxima en km/s amb que es pot injectar una partícula de càrrega q1 perquè no arribi a la línia L sinó que pugui voltar abans i impacti finalment en un punt de la línia de baix.
Primera edició: 12/2017. Segona edició: 09/2024.
Elaboració dels problemes i disseny d'aquest lloc web:
Antoni Amengual Colom, Departament de Física

El contingut d'aquest lloc web (text, imatges i vídeos) no es pot usar per fer-ne obres derivades. El contingut esmentat es pot usar amb finalitat educativa sense modificar, retallar o refer i sense ànim de lucre, citant sempre l'autor de les pàgines i posant en lloc visible l'adreça d'aquest lloc web. Usau: "GuiA Física · Antoni Amengual Colom · UIB url: dfs.uib.cat/apl/aac/fisicapbau/".

 Portada
Portada  Temes
Temes 
 Olimpíada
Olimpíada 

