
Camp magnètic


El flux d'un camp magnètic uniforme d'intensitat B a través d'una espira plana d'àrea S és
Φ = B S cos(α),
on α és l'angle que forma el camp magnètic amb la direcció perpendicular al pla de l'espira.
El flux pot canviar perquè:
canvia la intensitat del camp, B = B(t).
canvia l'àrea de l'espira, S = S(t).
canvia l'orientació relativa de l'espira i el camp, α = α(t).
Es consideraran casos on es produeix un canvi de només la intensitat, l'àrea o l'orientació.
Si el camp magnètic uniforme és perpendicular al pla d'una espira d'àrea S, el flux és
Φ = B S.
La unitat de flux magnètic en el Sistema Internacional d'Unitats és el Weber (Wb).

La llei de Faraday-Lenz s'escriurà en la forma
fem = −dΦ(t)/dt.
La llei de Faraday estableix que el canvi de flux de camp magnètic a través d'un circuit indueix un corrent elèctric en el circuit.
La llei de Lenz estableix que el sentit del corrent és tal que el camp magnètic a causa d'aquest corrent induït genera un flux que s'oposa al canvi de flux.
La llei de Faraday-Lenz reuneix les dues lleis.
Saber calcular la força electromotriu induïda en un circuit i saber determinar el sentit del corrent elèctric induït en una espira aplicant la llei de Lenz.
La força electromotriu s'indica en alguns llibres amb la lletra grega èpsilon (ε).
La unitat de força electromotriu el Sistema Internacional d'Unitats és el Volt (V). La força electromotriu no es mesura en newtons perquè no és una força en el sentit que tenen les forces dins la Física. Es denomina força perquè s'ha mantingut la denominació des de l'inici dels estudis de l'electricitat quan la paraula "força" s'usà perquè hi havia una causa que movia les càrregues elèctriques (electrons) en un circuit.


La llei de Lenz estableix que el sentit del corrent induït en un circuit quan canvia el flux de camp magnètic que el travessa, és aquell que s'oposa a la variació del flux.
Un fil conductor de 22 cm de longitud que té una resistència elèctrica de 300 Ω. Els extrems se solden i el fil es corba per formar una espira circular completa de 3.5 cm de radi.
L'espira es col·loca dins un camp magnètic uniforme perpendicular al pla de l'espira.
Determina el sentit del corrent induït, la força electromotriu i la intensitat del corrent elèctric a l'espira, quan la intensitat en tesles del camp magnètic canvia en funció del temps, expressat en segons, així:
a) B(t) = B0 + 0.60 t.
a) B(t) = B0 − 0.60 t.
B0 és un valor constant.
Demostración mostrar
Per donar el sentit del corrent, es considerarà que el camp magnètic apunta cap a fora del pla del dibuix, com es representa a la figura.

La intensitat del camp augmenta cap a fora del pla ⇒ El flux augmenta cap a fora del pla.
Oposar-se a l'augment de flux cap a fora ⇒ El corrent induït a l'espira ha de crear un camp cap a dedins ⇒ El corrent induít ha de tenir sentit horari.
Per la llei de Faraday-Lenz,
Φ(t) = B(t) Àrea = (B0 + 0.60 t) 0.00385 m2,
fem = −2.31 mV
El corrent elèctric és
I = |fem|/R = 2.331 mV / 300 Ω = 7.7 μA

La intensitat del camp disminueix cap a fora del pla ⇒ El flux disminueix cap a fora del pla.
Oposar-se a la disminució de flux cap a fora ⇒ El corrent induït a l'espira ha de crear un camp cap a fora ⇒ El corrent induït ha de tenir sentit antihorari.
La força electromotriu és 2.31 mV i la intensitat 7.7 μA.
ocultar
Una espira quadrada de costat 3 mm està dins un camp magnètic uniforme perpendicular al pla de l'espira. La intensitat del camp magnètic canvia sinusoïdalment amb una freqüència angular ω = 70 rad/s i un valor màxim B0 = 120 mT,
B(t) = B0 sin(ω t + π/3),
Calcula:
a) El flux de camp magnètic a través de l'espira en funció del temps.
b) La fem induïda a l'espira
c) Els tres primers instants després de t = 0 quan la fem és màxima.
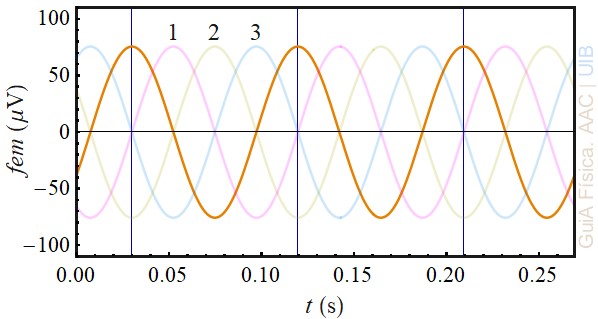
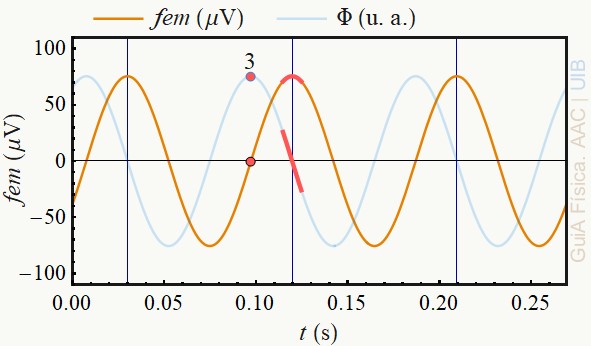
d) El gràfic següent mostra la força electromotriu en funció del temps i tres corbes de funcions sinusoïdals de la mateixa amplitud. Quina de les tres corbes representa correctament la variació del flux en funció del temps amb una determinada escala?
Resolució mostrar

L'àrea de l'espira és S = L2.
El flux de camp magnètic quan el camp és perpendicular al pla de l'espira és
Φ(t) = B S = B0 sin(ω t + π/3) L2
Usant els valors de l'enunciat s'obté
Φ(t) = 1.08 sin(70 t + π/3) μWb

Per la llei de Faraday-Lenz,

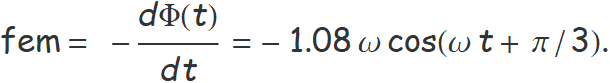
Amb els valors de l'enunciat,
fem = 75.6 cos(70 t + π/3) μV

Els primers instants després de t = 0 quan la força electromotriu és màxima corresponen als temps quan el cosinus val −1, això passa quan ω t + π/3 és igual a π més un múltiple de 2 π.
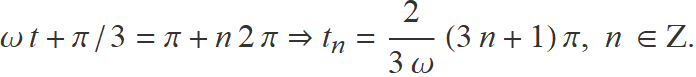
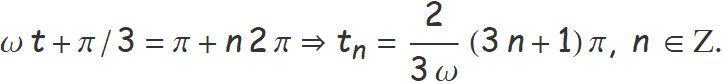
Els valors sencers n que donen els tres primers valors positius són 0, 1 i 2 :
t0 = 29.9 ms, t1 = 119.7 ms, t2 = 209.4 ms
Es pot comprovar que t2 − t1 i t1 − t0 són iguals a 2π/ω, que és el període de la funció sinusoidal.

El zeros de la corba de la força electromotriu han de coincidir amb els extrems de la corba del flux. Això no passa a la corba 1.
Pel signe negatiu de la llei de Faraday-Lenz, la força electromotriu és positiva i arriba al valor màxim quan la corba del flux decreix,
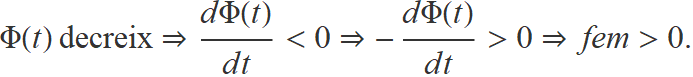
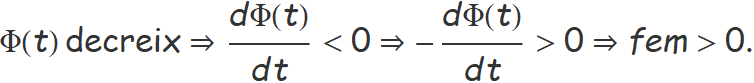
Això no passa a la corba 2.
La tercera corba compleix les dues condicions com ilustra la figura següent. Per tant,
La corba que representa correctament la variació del flux en funció del temps amb una determinada escala és la corba número 3

Un fil conductor recte es doblega en forma d'U de manera que la part corba és semicircular de 2 cm de radi. Una barra conductora rígida es col·loca sobre el fil doblegat com mostra la figura. La barra és perpendicular als braços del fil doblegat i passa inicialment pel centre de l'arc. S'estableix un camp magnètic perpendicular al pla del circuit i, a t = 0, la barra es comença a desplaçar cap a la dreta a 0.03 m/s
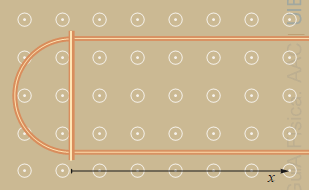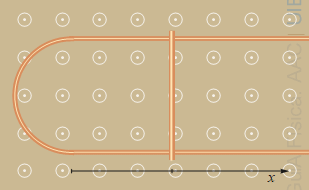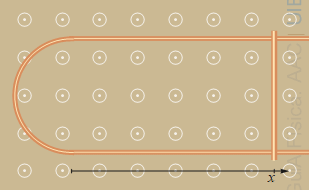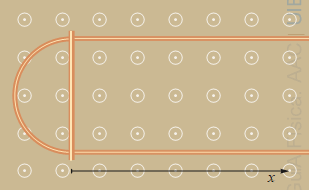
a) Escriu, en funció del temps, la posició x(t) de la barra i l'àrea S(t) que queda tancada entre la part esquerra de la U i la barra.
b) Determina el flux Φ(t) quan la intensitat del camp magnètic uniforme és de 0.7 T.
c) Calcula la força electromotriu induïda en el circuit que tanca la barra.
d) En quin sentit circula el corrent induït per la barra, segons la figura, de dalt a baix o de baix a dalt?
Resolució mostrar

Per un desplaçament de velocitat constant x(t) = x0 + v0 t, per tant, amb el temps en segons,
x(t) = 3 t cm
L'àrea tancada per la barra i la part esquerra de la U és igual a l'àrea del semicercle més l'àrea del rectangle de base x(t) i altura 2R = 4 cm. Amb el temps en segons,
S(t) = (2 π + 12 t) cm2 = (2 π + 12 t) 10−4 m2

Quan el camp magnètic uniforme és perpendicular al pla del circuit, el flux és B S(t). Amb el temps en segons,
Φ(t) = 0.7 T (2 π + 12 t) 10−4 m2 = (0.440 + 0.84 t) mWb

S'aplica la llei de Faraday-Lenz a la funció Φ(t) de l'apartat anterior. La derivada del flux és immediata.



Amb el desplaçament de la barra cap a la dreta, l'àrea S creix i, per tant, el flux de camp magnètic en la direcció cap a fora del pla de la figura augmenta.
Encara que l'espira formada per la barra i la part que queda a l'esquerra de la U no tengui forma circular, la regla de la mà dreta per determinar el sentit del camp magnètic a causa d'un corrent en el circuit es pot aplicar. El corrent induït ha d'anar en sentit horari perquè aquest corrent crearà un camp magnètic cap a l'interior del pla de la figura i s'oposarà a que augmenti el flux de camp magnètic.
Amb un corrent en sentit horari, el corrent per la barra ha d'anar
de dalt a baix
ocultar
Una espira circular de radi R té el centre a l'origen de les coordenades cartesianes. Inicialment, l'espira està continguda dins el pla x-z y el vector p perpendicular a l'espira que passa pel centre té la direcció i el sentit de l'eix y.
Es crea un camp magnètic uniforme en la direcció de l'eix y d'intensitat B0.
a) Determina el flux de camp magnètic a través de l'espira en funció de l'angle que forma el vector p i l'eix y.
b) L'espira es fa girar al voltant d'un diàmetre paral·lel a l'eix z a velocitat angular ω des de la posició inicial amb el vector p en la direcció de l'eix y. Que val l'angle α entre el vector p i l'eix y positiu en funció del temps?
c) Calcula la força electromotriu induïda a l'espira en funció del temps.
Resolució mostrar

El flux d'un camp magnètic uniforme d'intensitat B0 a través d'una espira plana d'àrea S és
Φ = B S cos(α),
on α és l'angle que forma el camp magnètic amb la direcció perpendicular al pla de l'espira. Es demana el flux en funció de l'angle que forma el vector p i l'eix y. Aquest angle és l'angle α perquè el vector el camp magnètic té la direcció de l'eix y i p és perpendicular al pla de l'espira.

L'angle α val 0 inicialment. Amb un gir a velocitat constant ω,
α = ω t

Quan l'espira gira a velocitat angular ω al voltant de l'eix z, el flux és
Φ(t) = B S cos(ω t).
Amb la llei de Faraday-Lenz, s'obté
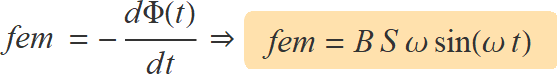
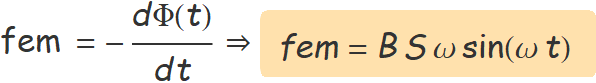


La unitat del flux magnètic en el Sistema Internacional, el Weber, (Wb) té el nom en honor al físic Wilhelm Eduard Weber. L'any 1856 publicà un article amb Rudolf Kohlrausch on apareixia la lletra c, inicial de la paraula llatina celeritas (velocitat), per primera vegada en premsa per indicar la velocitat de la llum.

1
La forma i les mides de dues espires es motren a la figura. L'espira de l'esquerra està formada per un fil que té dos arcs semicirculars i dos segments rectes que uneixen els extrems dels arcs. L'espira de la dreta està formada per un arc semicircular de 2 cm de radi, dos quarts d'arcs semicirculars de 4/3 cm de radi, i un segment recte a baix que tanca l'espira.

Les dues espires es col·loquen dins un camp magnètic uniforme amb la direcció del camp perpendicular al pla de les espires. Es necessita que el flux de camp magnètic a través de l'espira de l'esquerra sigui de 0.75 mWb i per això es regula la intensitat del camp magnètic.
a) Sense usar el valor de la intensitat del camp magnètic, determina el flux de camp magnètic a través de l'espira de la dreta quan el flux a través de l'espira de l'esquerra és 0.75 mWb.
b) Calcula la intensitat del camp magnètic perquè el flux a través de l'espira de l'esquerra sigui de 2 mWb.
2
El camp magnètic a l'interior d'un solenoide llarg, enfora dels extrems, és constant. La seva intensitat és μ0 n I, on n és el nombre de voltes del fil conductor per unitat de longitud. Determina la intensitat del corrent elèctric que ha de circular per un solenoide de 725 espires/cm per aconseguir el camp magnètic necessàri per crear un flux de 0.2 mWb a través d'una espira de 81 cm2.
3
Un fil conductor segueix el perímetre d'un rectangle de 21 cm2 dins un camp magnètic de 0.37 T. El pla del rectangle és perpendicular inicialment al camp magnètic, però després es gira al voltant d'un dels costats curts cap a dalt.
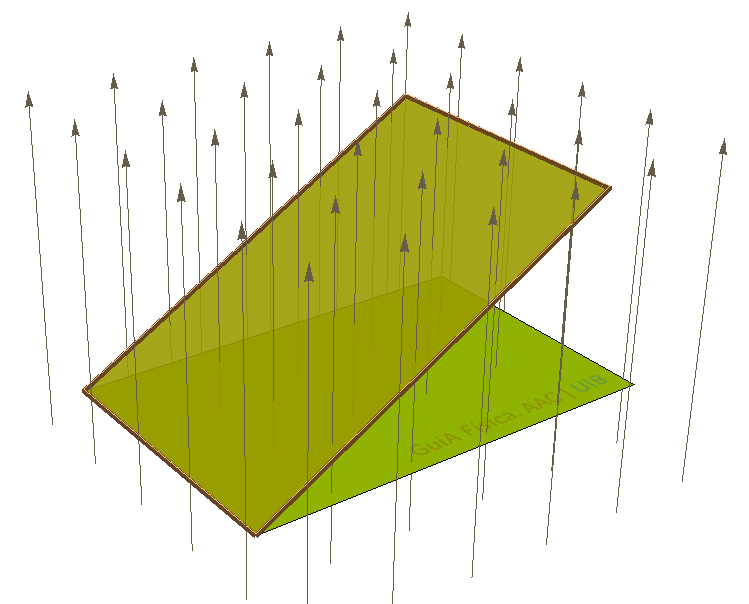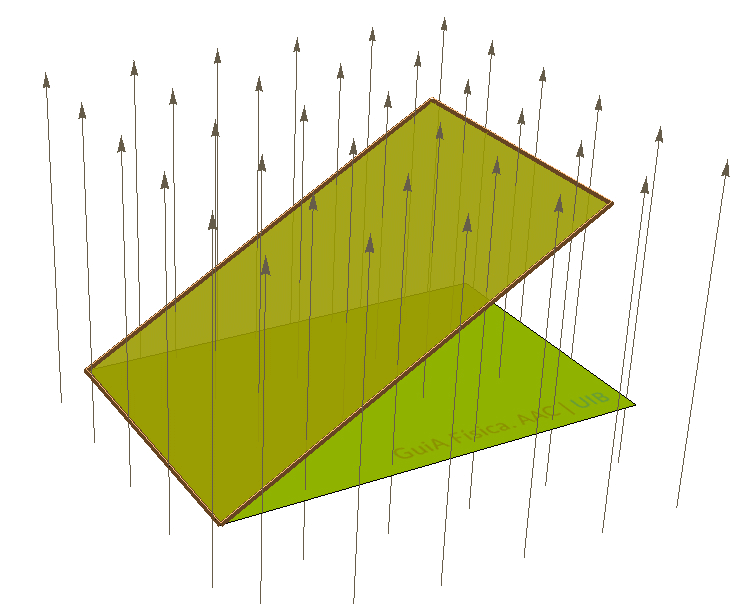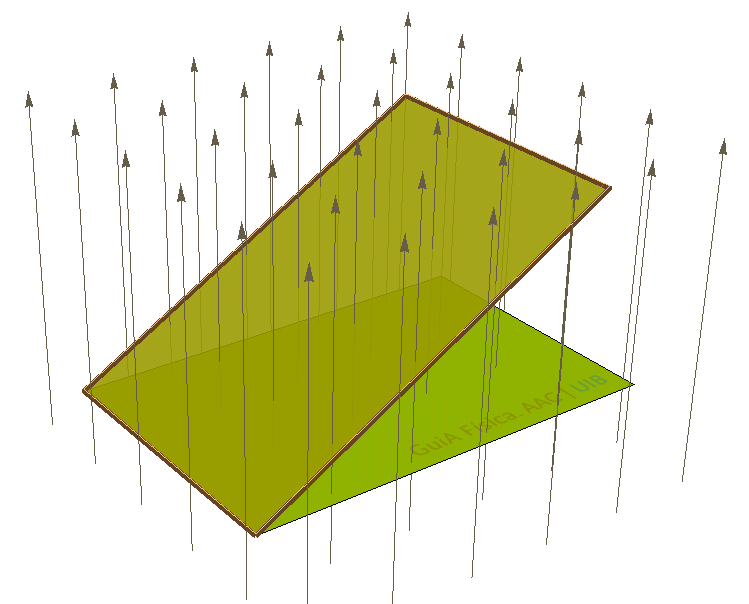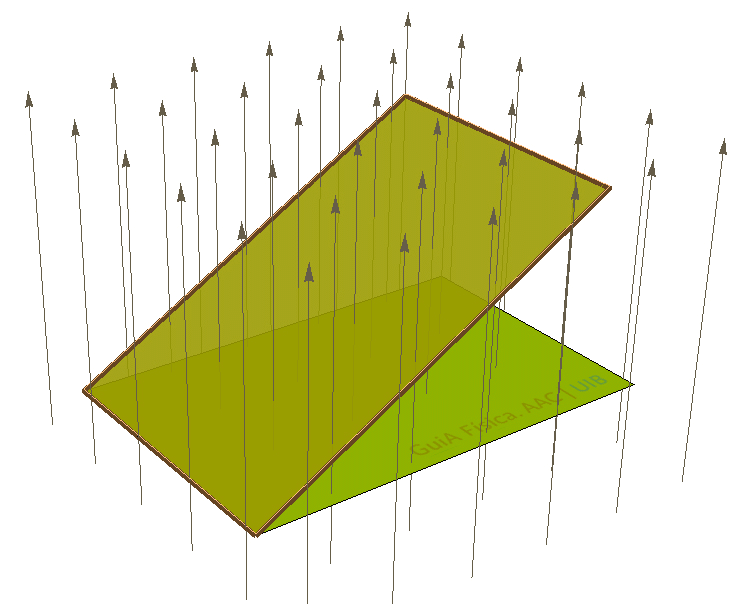
El flux de camp magnètic a través de l'espira que forma el fil conductor és de 777 μWb inicialment i de 765 μWb quan el rectangle està girat 10°. Comprova aquests dos resultats i calcula el flux quan el rectangle està girat 40° i 70°.
4
Una espira rectangular de 9 cm per 5 cm es troba sobre un pla dins un camp magnètic uniforme de 0.37 T que forma un angle θ1 amb la vertical de 42°. El flux de camp magnètic a través de l'espira és de 1237 μWb.

a) Comprova el valor del flux anterior i calcula els fluxos quan el camp magnètic forma angles de θ2 = 62° i θ3 = 82°.
b) Perquè els fluxos decreixen quan l'angle augmenta? (La resposta es mostrarà quan s'hagin obtingut els valors correctes de l'apartat a)
Resposta 4b
El flux és igual a B S cos(θ), on B és la intensitat del camp magnètic, S, l'àrea de la superfície tancada per l'espira i θ, l'angle que forma el camp magnètic amb la perpendicular a la superfície de l'espira. El seu valor estarà entre 0° i 90°.
Els fluxos decreixen quan l'angle augmenta perquè el cosinus de l'angle θ decreix quan l'angle creix.
Per a θ = 90°, el camp és paral·lel a l'espira i el flux és zero, no hi ha línies de camp que creuin la superfície tancada per l'espira.


Amb els seus experiments, Michael Faraday va descobrir els fenòmens d'inducció electromagnètica que són la base de la producció i la distribució de l'energia elèctrica a gran escala.


5
Es determina que apareix un corrent elèctric en sentit antihorari per una espira circular dins un camp magnètic. Quin o quins dels següents casos poden haver provocat aquest corrent elèctric?
1) El camp magnètic surt del pla de la figura i la seva intensitat està disminuint.
2) El camp magnètic entra en el pla de la figura i la seva intensitat està disminuint.
3) El camp magnètic surt del pla de la figura i la seva intensitat està creixent.
4) El camp magnètic entra en el pla de la figura i la seva intensitat està creixent.
