
Camp gravitatori


L'energia mecànica d'un objecte és la suma de l'energia cinética i l'energia potencia gravitatòria.
El principi de conservació de l'energia mecànica en un camp gravitatori estableix que l'energia cinètica i l'energia potencial poden canviar, però la suma de les dues es manté constant
Sigui M la massa d'una estrella o un planeta que crea el camp gravitatori dins el qual es mourà un objecte de massa m molt més petita (p.e. una sonda espacial), el principi de conservació de l'energia estableix


r1 = distància de m al centre de M,
v1 = velocitat de m quan està a la distància r1.
Encara que les energies se sumen, hi ha un signe menys davant el segon terme perquè l'energia potencial gravitatòria és negativa.

Si es té el valor de l'energia mecànica Em d'un objecte de massa m, es pot determinar:
i) La velocitat v2 quan l'objecte està a una distància r2.
ii) La distància r2 a la que estarà l'objecte quan la velocitat sigui v2.
S'ha de plantejar l'equació


i aïllar la incògnita, v2 o r2.
Donada la velocitat v1 a la distància r1 i v2 o r2, l'equació de la conservació de l'energia per aïllar la incògnita es pot plantejar directament i cancel·lar m, factor comú de tots els termes,

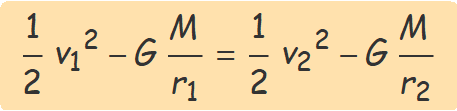

Per a una trajectòria radial allunyant-se de M, donat r1 i v1, es pot determinar si l'objecte de massa m arribarà o superarà una determinada distància r2 > r1 donada. El resultat depèn qualitativament del valor al que queda igualat v22 quan s'aïlla:
• v22 > 0 ⇒ l'objecte superarà la distància r2.
• v22 = 0 ⇒ v2 = 0 ⇒ l'objecte s'atura quan arriba a la distància r2 (després tornarà endarrere atret per M).
• v22 < 0 ⇒ L'arrel quadrada no dona un número real per a r2. L'objecte s'aturarà abans d'arribar a la distància r2.

La velocitat d'escapament ve del camp gravitatori d'un objecte de massa M des d'una distància r és la velocitat més més baixa perquè l'objecte s'allunyi indefinidament de M. Es calcula amb el principi de conservació de l'energia mecànica imposant que la velocitat de l'objecte s'hagi de fer zero a l'infinit:
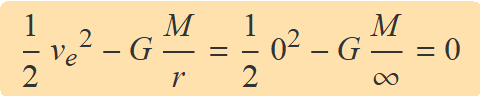

L'equació anterior permet aïllar


La velocitat d'escapament d'un planeta s'entén que és la velocitat d'escapament des de la superfície del planeta.


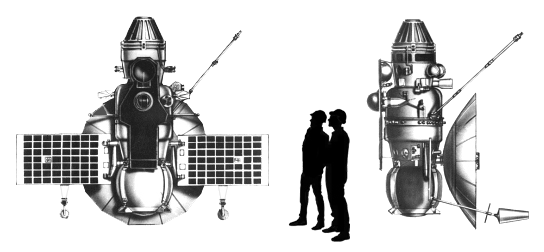
Les primeres sondes interplanetàries varen ser les Venera de la URSS que s'enviaren a Venus a la dècada dels anys 60 del segle XX. Tardaven uns tres mesos i mig en el trajecte fins al planeta. La primera sonda que aconseguí arribar a Venus va ser la Venera 3, però no aconseguí enviar dades. La Venera 4 va ser la primera en enviar dades mentre baixava però va quedar destruïda per les condicions de pressió i temperatura de l'atmosfera abans d'arribar a la superfície.
Una sonda enviada a Venus té una velocitat de 8.9 km/s a 9100 km del centre del planeta. Determina la velocitat de la sonda a 7000 km del centre usant el principi de conservació de l'energia mecànica. Cal considerar l'energia potencial respecte del Sol?
Dades:
MV (massa de Venus) = 4.867 1024 kg,
ms (massa de la sonda Venera 3) = 960 kg.
Resolució mostrar

El desplaçament de la sonda quan s'acosta a Venus és petit comparat amb la distància de Venus al Sol. Per això, el canvi d'energia potencial gravitatòria de la sonda entre les dues posicions respecte del Sol és negligible.
L'equació de conservació de l'energia és


La massa de la sonda es pot simplificar,
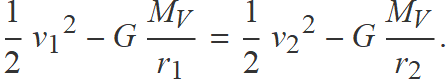
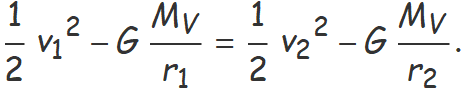

Les variables s'han d'expressar en metres quan s'usa el valor habitual de la constant de gravitació universal G perquè les unitats inclouen metres.
v1 = 8.9 × 103 m/s,
r1 = 9.1 × 106 m,
v2 = incògnita,
r2 = 7.0 × 106 m.
Amb els valors dins l'equació (1), es té
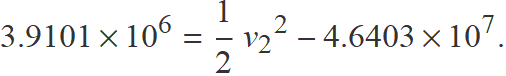
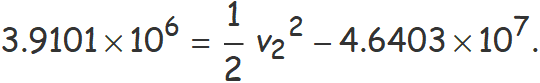
Aïllant s'obté
v2 = 10031 m/s ⇒ v2 = 10.0 km/s
ocultar
Per tornar a la Terra, els astronautes Neil Armstrong i Michael Collins que estaven a la superfície de la Lluna en la missió Apollo 11 l'any 1969 havien de pujar amb el mòdul lunar Eagle fins a al mòdul Columbia, tripulat per Buzz Aldrin, que els esperava orbitant a 100 km d'altura.

El mòdul Eagle es va enlairar amb una trajectòria corba per posar-se a la mateixa òrbita del Columbia, uns cinc cents kilòmetres darrera. Després s'hi va anar apropant fins acoplar-se. El mòdul no va anar en direcció radial des de la Lluna per trobar-se amb la Columbia directament, però suposar un enlairament radial permet fer un càlcul bàsic per tenir una mida de la velocitat d'enlairament necessària. Així es planteja el següent:
Calcula la velocitat inicial mínima en direcció radial perquè un mòdul de 15000 kg parteixi de la superfície de la Lluna i, sense propulsió addicional, arribi a 100 km d'altura.
Expressa la velocitat en km/h.
Dades:
RL (radi de la Lluna) = 1737 km,
ML (massa de la Lluna) = 7.348 × 1022 kg.
Resolució mostrar
La velocitat inicial mínima en direcció radial és aquella amb que la nau arriba a 100 km d'altura amb velocitat zero. Si la nau parteix amb una velocitat inferior, no arribarà als 100 km; i si parteix amb una velocitat superior, depassarà aquesta altura.
Com que la nau no té propulsió addicional, s'aplicarà el principi de conservació de l'energia,
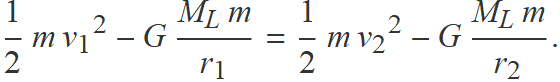
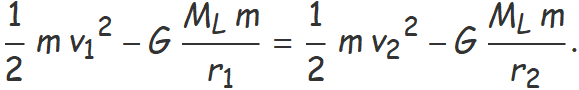
La massa m de la nau es pot simplificar.
Les variables s'han d'expressar en metres per les unitats de G que inclouen metres.
v1 = incògnita,
r1 = RL = 1737 × 103 m,
v2 = 0,
r2 = RL + 100 km = 1837 × 103 m.
Substituint els valors dins l'equació (2) es té
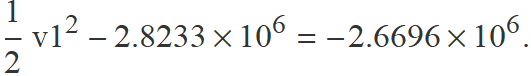
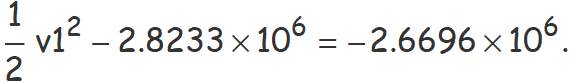
Aïllant v1 s'obté la velocitat en km/s que es passa a km/h fàcilment,
v1 = 0.554 km/s ⇒ v1 = 1966 km/h
ocultar
Un objecte es llança verticalment a 300 m/s des de la superfície de la Lluna. Arribarà l'objecte a 40 km d'altura?
Dades:
RL (radi de la Lluna) = 1737 km,
ML (massa de la Lluna) = 7.348 × 1022 kg.
Resolució mostrar
S'aplicarà el principi de conservació de l'energia,
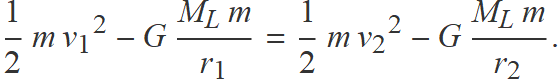

La massa m de l'objecte es pot simplificar.
Les variables s'han d'expressar en metres per les unitats de G que inclouen metres.
v1 = 300 m/s,
r1 = RL = 1737 × 103 m,
v2 = 0 (l'objecte s'atura i caurà),
r2 = RL + 40 km = 1777 × 103 m.
Substituint els valors dins l'equació (3) es té
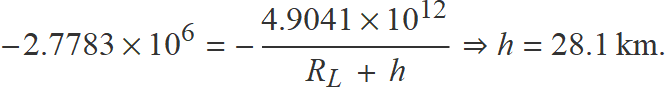

L'objecte puja fins a 28.1 km d'altura i després torna caura.
NO arriba als 40 km
ocultar
Calcula la velocitat d'escapament de la Terra.
Dades:
RT (radi de la Terra) = 6370 km,
MT (massa de la Terra) = 5.9722 × 1024 kg.
Resolució mostrar
La velocitat d'escapament es calcula amb el principi de conservació de l'energia mecànica imposant que la velocitat de l'objecte que escapa sigui zero a l'infinit.
La massa de l'objecte es pot simplificar de l'equació de conservació de l'energia:
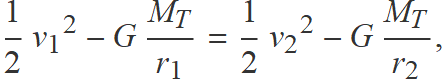

Amb
r1 = RT,
v1 = ve (velocitat d'escapament),
r2 = ∞,
v2 = 0,
l'Eq. (4) queda
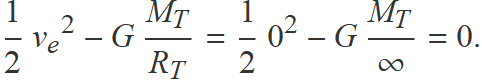
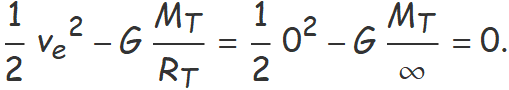
Aïllant ve resulta,





1
Una sonda es mou radialment cap el centre de Venus a 10.1 km/s quan es troba a 8000 km del centre del planeta.
Calcula la velocitat de la sonda quan es trobi a 6500 km del centre de Venus.
MVenus = 4.867 1024 kg,
2
Una sonda es dirigeix en línia recta cap el centre d’una lluna sense atmosfera, de la mateixa mida que la nostra lluna (3476 km de diàmetre) però de 5.0 × 1022 kg de massa. La sonda es mou a 7.9 km/s quan es troba a 8700 km de la superfície d’aquesta lluna. Calcula la velocitat de la sonda quan impacti sobre la superfície.
3
Una sonda espacial s'allunya radialment de la Terra.
A 72000 km del centre de la Terra i amb els propulsors apagats, es mou a 3 km/s. Fins a quina distància màxima del centre de la Terra arribarà?
Dades: MT (massa de la Terra) = 5.9722 × 1024 kg.
4
Quines de les definicions següents descriuen correctament la velocitat d'escapament?
a) La velocitat d'escapament fa referència a la velocitat mínima que un objecte ha d'assolir per alliberar-se de l'atracció gravitacional d'un cos celeste i no tornar-hi a caure.
b) S'entén per velocitat d'escapament la rapidesa necessària que ha de posseir un projectil o un vehicle per poder superar la força gravitacional d'un planeta, aconseguint així desprendre's de la influència gravitacional.
c) És la velocitat mínima que un objecte necessita assolir per romandre en una òrbita fixa al voltant d'un planeta sense caure a la seva atmosfera
d) La velocitat d'escapament és el llindar de velocitat que permet a un objecte sortir de l'atmosfera d'un astre i entrar a l'espai exterior sense tornar a ser atret cap a la superfície.
5
Calcula la velocitat d'escapament del Sol des de:
a) La superfície solar.
b) L'òrbita terrestre a 1 au de distància.
Dades:
RS (radi del Sol) = 696340 km,
MS (massa del Sol) = 1.9891 × 1030 kg,
1 au = 149597871000 m.
