
Òrbites circulars


Les òrbites circulars són un cas particular d'òrbites el·líptiques.
L'altura d'una òrbita és el radi de l'òrbita menys el radi del planeta.
La velocitat d'un satèl·lit de massa m en una òrbita circular de radi r al voltant d'un planeta de massa M es calcula igualant la força centrípeta a la força d'atracció gravitatòria,


La relació anterior de la velocitat amb el radi, fa que l'energia cinètica, i l'energia mecànica total del satèl·lit tenguin relacions senzilles amb l'energia potencial


Energia cinètica en funció de l'energia potencial:


Energia mecànica total en funció de l'energia potencial:


L'energia potencial d'un satèl·lit en una òrbita circular és negativa i l'energia mecànica total també és negativa.

L'òrbita geoestacionària (GEO, sigles de l'anglès GEostationary Orbit) és la dels satèl·lits que sempre estan sobre un mateix punt de l'equador terrestre.

Un satèl·lit en l'òrbita geoestacionària es manté en un punt fix del cel sobre l'horitzó. Per això, se solen usen per a telecomunicacions. Les antenes parabòliques, que han de captar la senyal d'un satèl·lit geoestacionari poden ser fixes (les antenes parabòliques dels terrats o balcons de les cases solen ser fixes; si alguna és mòbil és per orientar-la cap a més d'un satèl·lit).
Un satèl·lit s'ha de moure a velocitat constant per mantenir-se en un punt fix del cel. Per tant, l'òrbita geoestacionària ha de ser circular.
La força centrípeta que genera l'òrbita circular ha de ser la força d'atracció gravitatòria de la Terra. Per tant, la força centrípeta ha d'apuntar al centre de la Terra, de manera que l'òrbita ha estar continguda en el pla de l'equador terrestre.
La velocitat angular del satèl·lit ha de ser igual a la de rotació de la Terra. El període orbital és el període de rotació de la Terra
T ≈ 23 h, 56 min i 4 s.
T és le dia sideral i no és 24 h, perquè 24 h és el dia solar: Com que la Terra rota i orbita el Sol, els dos temps no coincideixen. (veure explicació)
La velocitat vg del satèl·lit i el radi Rg de l'òrbita geoestacionària estan relacionades per dues equacions:
i) La força centrípeta és igual a la força d'atracció gravitatòria com passa en qualsevol satèl·lit en òrbita circular. D'on s'aïlla la velocitat. Sigui Mt la massa de la Terra:


ii) La velocitat és la longitud de l'òrbita dividida pel període orbital T de la Terra.


Les Eqs. (1) i (2) permeten aïllar la velocitat i el radi de l'òrbita geoestacionària.


L'òrbita geoestacionària és única. Els satèl·lits geoestacionaris s'han de situar separats sobre aquesta òrbita circular per evitar interferències en les transmissions. Això limita el nombre de satèl·lits que poden seguir aquesta òrbita.
La Terra no crea un camp gravitatori perfectament esfèric perquè el planeta no és una esfera uniforme. A més, el Sol i la Lluna contribueixen al camp gravitatori en els punts de l'òrbita geoestacionària. Aquestes i altres causes fan que els satèl·lits GEO s'hagin de propulsar períodicament per corregir la seva posició i mantenir-la geoestacionària. Quan un satèl·lit acaba el combustible, acaba sortint de l'òrbita geoestacionària. La vida útil de cada satèl·lit està limitada per la quantitat de combustible que porta.


L'òrbita de l'Estació Espacial Internacional (EEI) (vegeu imatge) té el perigeu a 413 km d'altura i l'apogeu a 422 km.

Calcula el període orbital en minuts i la velocitat en km/h respecte de la Terra d'una estació que seguís una òrbita circular de 418 km d'altura. El període i la velocitat d'aquesta estació serien pràcticament iguals a les de l'EEI.
Rt (radi equatorial de la Terra) = 6378.1 km,
Mt (massa de la Terra) = 5.97217 × 1024 kg.
S'usaràn t en el subíndex perquè T serà el símbol per al període i no per a la Terra.
Resolució mostrar
Perquè una estació de massa m segueixi una òrbita circular de radi R, la força centrípeta ha de ser constant i és igual a la força d'atracció gravitatòria


Aïllant la velocitat, s'obté

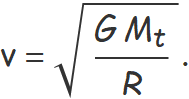
El radi de l'òrbita és el radi de la Terra més l'altura de l'òrbita,
R = Rt + 418 km.
Llavors,


El període orbital es pot calcular dividint la longitud de l'òrbita per la velocitat



a) Calcula el radi i l'altura de l'òrbita geoestacionària amb les dades
Rt (radi equatorial de la Terra) = 6378.1 km,
Mt (massa de la Terra) = 5.97217 × 1024 kg,
T (període de rotació de la Terra) = 23 h 56 min 4.10 s = 86164 s.
b) En un dibuix, un cercle de 2.575 cm de diàmetre (com una moneda de dos euros) representa la Terra. Quin és el diàmetre del cercle que representa l'òrbita geoestacionària amb la mateixa escala?
c) Fes un dibuix a escala amb un cercle que representa la Terra i dues línies per representar el radi i l'altura de l'òrbita geoestacionària.
Resolució mostrar

Sigui
Rg = radi de l'òrbita geoestacinària,
T = període orbital = període de rotació de la Terra
m = massa del satèl·lit,
vg = velocitat del satèl·lit,
Mt = massa de la Terra.
La velocitat del satèl·lit geoestacionari és igual a la longitud de l'òrbita de radi Rg dividida pel període orbital


La força centrípeta sobre el satèl·lit és l'atracció gravitatòria de la Terra,


Aïllant Rg entre les dues equacions es troba


Llavors,


Usant els valors numèrics de l'enunciat i que l'altura de l'òrbita és Rg − RT, s'obté
Rg = 42164 km
hg = 35786 km

La mida del diàmetre de l'òrbita geoestacionària en el dibuix a escala es determina amb la regla de tres:
2.575 cm → 2 RT,
x cm → 2 Rg.
La solució és
x = 17.023 cm


Calcula a quina velocitat en km/h es mou respecte de la Terra un satèl·lit en òrbita geoestacionària. Justifica el càlcul del radi d'aquesta òrbita.
Dades de la Terra:
Rt (radi equatorial) = 6378.1 km,
Mt (massa) = 5.97217 × 1024 kg,
T (període de rotació) = 23 h 56 min 4.10 s = 86164 s,
Resolució mostrar
Perquè un satèl·lit segueixi una òrbita circular de radi R, la força centrípeta ha de ser constant i igual a la força d'atracció gravitatòria,


Aïllant la velocitat, s'obté


En el temps d'un període orbital T, el satèl·lit ha de recórrer una circumferència de radi R, llavors
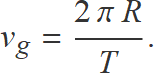
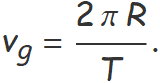
Igualant les Eqs. (4) i (5) es pot aïllar R,


Perquè l'òrbita circular sigui geoestacionària el període del satèl·lit és igual al període de rotació de la Terra. Amb les dades de l'enunciat es determina que el radi de l'òrbita geoestacionària es
R = 42164 km.
La velocitat del satèl·lit serà
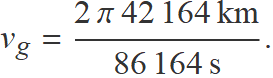

El resultat és
v = 11.07 km/s
ocultar
A l'examen de Física de les proves d'accés a la universitat, no es podrà projectar un vídeo com a l'examen d'Arts escèniques. Però, si es pogués projectar un vídeo, podria ser un com el següent i es podria demanar descriure les fases de com es dirigeix un satèl·lit a l'òrbita geoestacionària.
El vídeo de poc menys de set minuts presenta el satèl·lit Hispasat 30W-5, llançat el 29 de desembre de 2010 per l'empresa espanyola operadora de satèl·lits de comunicacions del mateix nom. Mira el vídeo encara que la pregunta no hagi de sortir a l'examen d'accés.

L'òrbita estacionaria sobre un punt de l'equador de Mart es denomina òrbita areostacionària pel deu grec Ares, l'equivalent a Mart en la mitologia romana.
A la imatge, es representa Mart i l'òrbita areostacionària a la mateixa escala que la Terra i l'òrbita geoestacionària. Actualment, no hi ha cap satèl·lit en òrbita areostacionària, però s'ha representat el moviment d'un satèl·lit en aquesta òrbita amb la mateixa escala de temps que el d'un satèl·lit geoestacionari.


Calcula a partir de lleis físiques el radi i l'altura de l'òrbita areostacionària.
Dades de Mart:
M (massa) = 6.4171 1023 kg,
Req (radi equatorial) = 3396 km,
T (període de rotació) = 24 h 37 min 22 s.
Resolució mostrar
Sigui
Ra = radi de l'òrbita areoestacinària,
m = massa del satèl·lit,
vg = velocitat del satèl·lit.
La velocitat del satèl·lit areoestacionari és igual a la longitud de l'òrbita de radi Ra de l'òrbita dividida pel període orbital


La força centrípeta sobre el satèl·lit és l'atracció gravitatòria de Mart,


Aïllant Ra entre les dues equacions es troba


L'altura de l'òrbita areostacionària és
ha = Ra − Req = 17032 km


El satèl·lits artificials que tenen òrbita circular són el geoestacionaris. La majoria de satèl·lits tenen òrbites el·líptiques.

1
Un satèl·lit té l'òrbita circular al voltant de la Terra a una altura de 200 km i es mou a una velocitat v1 respecte del centre de la Terra. Un altre satèl·lit orbita 600 km d'altura i es mou a una velocitat v2. Què val el quocient v1v2?
Rt (radi equatorial de la Terra) = 6378.1 km,
Mt (massa de la Terra) = 5.97217 × 1024 kg.
2
Es vol posar en òrbita circular i en el pla de l'equador, un satèl·lit perquè passi sobre Quito, capital de l'Equador, cada 12 h. Calcula a quina altura orbitarà el satèl·lit i amb quina velocitat es mourà respecte del centre de la Terra?

3
L'energia potencial gravitatòria d'un satèl·lit en òrbita circular al voltant de la Terra val −5.4 1010 J. Què val l'energia cinètica del satèl·lit?
4
Un satèl·lit en òrbita circular té una energia mecànica total de −6.4 1010 J. Què val l'energia potencial gravitatòria del satèl·lit?
5
L'energia cinètica d'un satèl·lit de 1210 kg en òrbita circular al voltant de la Terra val 2.41 1010 J. Quin és el radi de l'òrbita?
MT (massa de la Terra) = 5.9722 × 1024 kg.
