
Camp gravitatori


La unitat astronòmica
Símbol: au (símbol internacional del nom en anglès)
Valor: 1 au = 149597870700 m
La unitat astronòmica és una constant equivalent a la distància mitjana entre el Sol i la Terra.

Equació
Els punts (x, y) d'una el·lipse centrada a l'origen de coordenades amb el semieix major de longitud a sobre l'eix x i el semieix menor de longitud b sobre l'eix y, compleixen l'equació
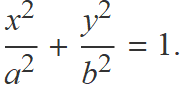
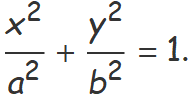
Focus
Els focus d'una el·lipse són els dos punts de l'eix major a una distància c del centre de l'el·lipse, tal que c2 = a2 − b2
c2 = a2 − b2.

Una característica dels focus és que la suma de les distàncies d'un punt de l'el·lipse als focus és constant i igual a 2a. Si qualsevol punt P de l'el·lipse,
distància(F', P) + distància(F, P) = 2a.
(Quan es tractin les lleis de Kepler, cal fixar-se que la lletra a cursiva és el símbol usat per a la longitud del semieix major d'una el·lipse i la lletra a sense cursiva és el símbol d'any.)
Excentricitat (ε)
L'excentricitat d'una el·lipse és
ε = c / a
(ε és la lletra grega èpsilon). Per la definició de c, l'excentricitat és petita quan b ≈ a i l'el·lipse és quasi una circumferència.

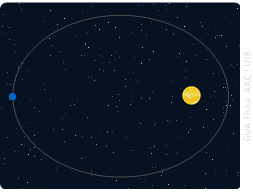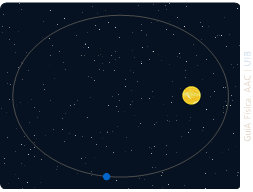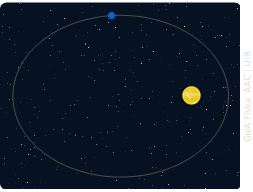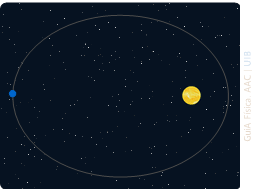
Primera llei o llei de les òrbites
Els planetes segueixen òrbites el·líptiques
amb el Sol en un dels focus
Segona llei o llei de les àrees
El segment entre el Sol i un planeta escombra
àrees iguals en temps iguals
Tercera llei o llei dels períodes
El quadrat del període orbital d'un planeta és
directament proporcional
al cub del semieix major de la seva òrbita

Les lleis es diuen lleis de Kepler perquè les va formular l'astrònom alemany Johannes Kepler entre 1609 i 1619 analitzant les meticuloses observacions de l'astrònom danès Tycho Brahe. Brahe va reunir les dades més precises de les posicions dels cossos celestes abans de la invenció del telescopi.
La primera llei va ser revolucionària perquè la idea predominant, arrelada des de l'antiguitat, era que els planetes es movien seguint circumferències perfectes al voltant del Sol.

El periheli és el punt d'una trajectòria més proper al Sol.
L'afeli és el punt d'una òrbita el·líptica més enfora del Sol.
Perigeu és el punt més proper al centre de la Terra d'una òrbita al voltant de la Terra i l'apogeu el més llunyà.
Periastre i apoastre són els noms genèrics dels punts d'una òrbita més proper i més llunyà, respectivament, al centre d'atracció.
La suma de les distàncies del periastre i l'apoastre al centre de forces és dues vegades la longitud del semieix gran. Si les distàncies s'indiquen per rp i ra, respectivament, es té
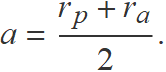
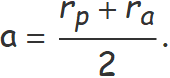

La velocitat areolar és el quocient entre l'àrea escombrada pel segment entre el Sol i un planeta durant un temps donat, dividida per aquest temps.
La segona llei de Kepler o llei de les àrees es es pot anunciar també així
Cada planeta es mou amb velocitat areolar constant
Cada parella de línies radials consecutives des del centre del Sol delimiten, amb la línia de la trajectòria el·líptica, àrees iguals.

El temps que tarda un planeta o un cometa en anar d'A a B prop del periheli (PH) és el mateix que tarda en anar de DC prop de l'afeli (AF).
Els planetes i els cometes es mouen més ràpid quan són més a prop del Sol i més lentament quan estan més allunyats.

Saber resoldre problemes amb la tercera llei.
Saber que les lleis de Kepler es varen deduir per al sistema solar però també s'apliquen al sistema de llunes de planetes grans. La constant de la tercera llei depèn de la massa del cos central (el Sol o el planeta).

Johannes Kepler va usar les dades de les observacions de Mart de Tycho Brahe per establir les lleis per aquest planeta. Després es va veure que les lleis es podien aplicar a tots els planetes coneguts. Quan, més tard, Isaac Newton va deduir matemàticament les lleis amb les seves teories de la gravitació i de la Mecànica, però havia de negligir la massa dels planetes en front a la massa del Sol i la interacció gravitatòria entre els planetes. Per tant, les lleis de Kepler en el sistema solar són aproximades.
Mercuri és el planeta més proper al Sol i la seva òrbita no és exactament el·líptica. La posició del periheli es desplaça i no es va poder explicar amb la teoria de la gravitació de Newton. El desplaçament no es va poder calcular correctament fins que es va usar la teoria general de la relativitat.


Newton va deduir que T2/a3 era constant en el sistema solar negligint la massa dels planetes en front a la del Sol.
Haver negligit la massa dels planetes és un motiu perquè la tercera llei de Kepler no es compleixi exactament.
Newton també usà que cada planeta estava subjecte únicament a la gravetat del Sol, però els planetes tenen interaccions gravitacionals entre ells. Aquestes interaccions afecten la trajectòria i, per tant, els períodes orbitals. Per exemple, la gravetat de Júpiter té un impacte notable a les òrbites d'altres planetes. Aquest és un altre motiu pel qual la tercera llei de Kepler no es compleix exactament.
A la Taula següent es presenten els períodes orbitals i els semieixos grans de les òrbites dels planetes del sistema solar. Calcula T2 / a3 per a cada un dels planetes.
| Planeta | T (any) | a (ua) | T2 / a3 |
| Mercuri | 0,241 | 0,3871 | |
| Venus | 0,615 | 0,7233 | |
| Terra | 1 | 1,00 | 1.00 |
| Mart | 1,88 | 1,524 | |
| Júpiter | 11,86 | 5,204 | |
| Saturn | 29,46 | 9,582 | |
| Urà | 84,01 | 19,229 | |
| Neptú | 164,8 | 30,104 |
Quins dels valors de T2 / a3 es diferencia més d'1?

El gener de 2022 es descobrí l’asteroide 2022 AP7 que té una part de l’òrbita prop de l’òrbita terrestre. No es coneix la massa i se li atribueixen unes dimensions de l'ordre d'un quilòmetre i mig. Les mides de les òrbites de l'asteroide 2022 AP7, Mart i la Terra s'han dibuixa a escala a la figura.
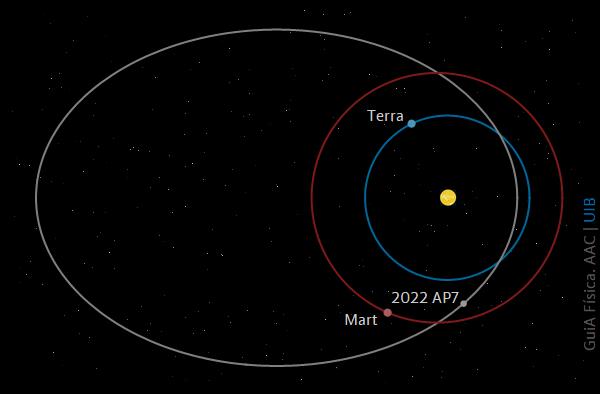
El semieix major de l’òrbita terrestre fa 1 au i el de l’asteroide, 2.924 au. Calcula el període orbital en anys de l’asteroide aplicant una llei de Kepler.
Resolució mostrar
L'asteroide es mou per l'atracció del Sol. Lluny dels planetes segueix una trajectòria el·líptica d'acord amb les lleis de Kepler.
S'aplicarà la tercera llei de Kepler per calcular el semieix major de l'òrbita de l'asteroide 2022 AP7. La tercera llei estableix que el quocient entre el quadrat del període orbital dividit pel cub del semieix major de l'òrbita és constant per a tots els planetes i cometes que segueixen òrbites el·líptiques al voltant del Sol,
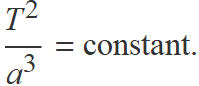
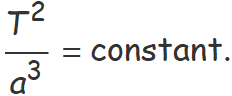
Si s'usa l'any com a unitat de temps i la unitat astronòmica com a unitat de longitud, el valor numèric del quocient per a la Terra és 1 i també ho ha de ser per a l'asteroide,
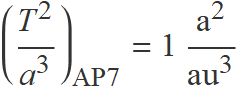
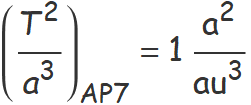
D'aquí es pot aïllar el període orbital de l'asteroide en funció del semieix major de la seva òrbita,

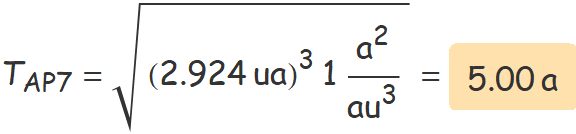

Isaac Newton va deduir les lleis de Kepler calculant el moviment d'una massa atreta per una altra molt més gran. Per tant, les lleis de Kepler s'apliquen a tots els cossos que es mouen dins el camp gravitatori d'un únic objecte de massa molt més gran.
Les lleis de Kepler es poden aplicar, sabent que serà una aproximació, a les òrbites de les llunes d'un planeta gran com Júpiter perquè l'atracció del planeta és més gran que la del Sol. El valor constant de T2/a3 per a les llunes que orbiten el planeta serà al valor de la constant per als cossos que orbiten el Sol.
Galileu va descobrir les quatre llunes més grans de Júpiter l'any 1610. D'aquestes, la lluna més propera a Júpiter és Io, però la més propera és Metis descoberta l'any 1979 per les fotografies enviades per la sonda Voyager I. Les òrbites de Metis i de Io són quasi circulars. Júpiter i els radis de les òrbites de Metis i de Io estan dibuixats a escala a la figura.

Determina el període orbital en hores de Metis usant la tercera llei de Kepler i el període orbital d’Io, que és d’1 dia i 18.5 hores.
Resolució mostrar
La tercera llei estableix que el quocient entre el quadrat del període orbital dividit pel cub del semieix major de l'òrbita és el mateix per a les dues llunes.
Usant com unitat de temps l'hora i com a unitat de longitud el quilòmetre, es pot calcular la constant
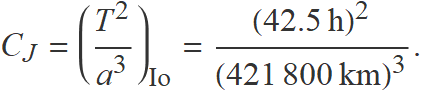

El període orbita de Metis serà
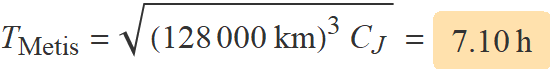



Johannes Kepler (1571-1630), astrònom i matemàtic alemany. Va descobrir les lleis sobre el moviment dels planetes. Les seves obres més influents varen ser Astronomia Nova i Harmonices Mundi.

1
Quina de les següents afirmacions, relacionades amb la segona llei de Kepler, és falsa?
a) Un planeta es mou més ràpid quan és més a prop del Sol i més lentament quan és més lluny.
b) L'àrea escombrada pel segment que uneix el planeta amb el Sol és proporcional al temps transcorregut des d'un instant inicial.
c) La segona llei de Kepler també es pot aplicar a les òrbites d'un conjunt de llunes properes a un planeta molt gran.
d) La segona llei de Kepler mai s'aplica als cometes.
Les tres lleis de Kepler s'apliquen a un objecte que orbita un únic altre objecte més massiu. Llavors, un cometa no es mou seguint les lleis de Kepler si passa prop d'un planeta i l'atracció gravitatoria d'aquest no és molt més petita que la del Sol; però el cometa si que es mou d'acord amb les lleis de Kepler lluny dels planetes. Per això, l'afirmació (d) és falsa. No es cert que la segona llei mai s'apliqui als cometes.
2
Considera la superfície tancada pel radi imaginari del Sol a la Terra l'1 de gener, el radi imaginari del Sol a la Terra el 31 de gener i l'arc de l'òrbita terrestre entre aquestes dues dates. L'àrea A d'aquesta superfície en km2 és enorme.
Es pot saber quina és l'àrea tancada per l'òrbita de la Terra en funció d'A?
Si es pot saber, quina àrea és?
a) No es pot saber
b) 365 A
c) 24 A
d) 12 A
3
Newton va deduir què havia de valer el quocient entre el quadrat del període orbital i el cub del semieix major de l'òrbita el·líptica, que Kepler havia dit era constant per als planetes del sistema solar.
El càlcul de Newton per a un planeta aïllat que orbita el Sol tingué el resultat:
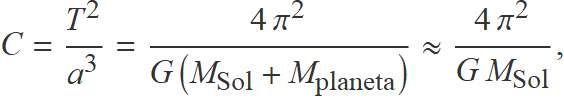

resultat independent del planeta si la massa del Sol és molt més gran que la de qualsevol planeta.
Si s'usa l'any com a unitat de temps i la unitat astronòmica com a unitat de longitud, el valor numèric del quocient per a la Terra és 1.
a) Calcula el valor de C en s2 / m3 amb la massa del Sol.
MSol = 1.98848 × 1030 kg,
G = 6.6743 10−11 N m2 kg−2.
b) Passa el resultat a les unitats a2 / ua3 per verificar que el valor numèric de C amb aquestes unitats és 1.
4
El cometa Halley duu el nom d'Edmund Halley, un amic de Newton, perquè va identificar que les observacions d'uns cometes anteriores corresponien al mateix cometa que era visible quan s'acostava al Sol de manera períodica.
Es determina que el cometa Halley té el periheli a 0.59 au i l'afeli a 35 au, quin és el període orbital en au del cometa al voltant del Sol a partir d'aquestes dades segons una llei de Kepler?
Edmund Halley va predir quan tornaria ser visible un cometa en el cel. Això havia de ser unes dècades més tard. El cometa va aparèixer just l'any després del que havia predit Halley.
L'òrbita del cometa va fins més enllà de Neptú. Quan el cometa avança i passa prop d'algun dels planetes grans, l'òrbita es veu modificada per l'atracció del planeta, modificant un poc l'òrbita i, per tant, la periodicitat orbital. Per això, l'aparició del cometa no és totalment regular i s'endarrerí un any respecte a la data que havia donat Edmund Halley.
El cometa tornarà ser visible en el cel a simple vista l'any 2061.
5
Júpiter i les posicions de les seves llunes Io i Tebe en els periastres s’han dibuixat a escala a la figura. Les fletxes sobre l’escala indiquen les distàncies de Tebe al centre de Júpiter quan passa pel periastre i l’apoastre.

Les lleis de Kepler s’apliquen als planetes que orbiten una estrella o a les llunes que orbiten un planeta gros com Júpiter. Enuncia la segona llei de Kepler referida al sistema solar.
Io té un període orbital d’1 dia i 18.5 hores i el semieix major de la seva òrbita fa 421800 km. Determinau el període orbital en hores de Tebe amb la tercera llei de Kepler aplicada al sistema de llunes de Júpiter.
