Camp gravitatori
Charles-Augustin de Coulomb es va basar en la llei de Newton per establir la llei que duu el seu nom i la va comprovar amb mesures experimentals.
La forma matemàtica de la força d'atracció gravitatòria entre dues partícules i la d'atracció o repulsió entre partícules amb càrregues elèctriques és la mateixa. La presència del signe menys davant G indica que la força sempre és atractiva, mentre que la força elèctrica serà repulsiva si les càrregues tenen el mateix signe i atractiva si tenen signes contraris.
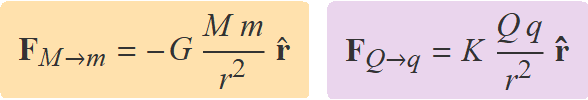
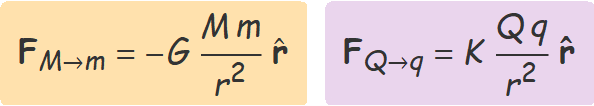
r = vector de M a m o de Q a q.
r = mòdul de r = distància entre M i m o Q i q,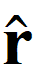
= r / r (vector unitari o de mòdul 1 paral·lel a r).
Evidentment, la forma matemàtica del camp gravitatori i del camp elèctric també és la mateixa. La presència del signe menys davant G indica que el camp és atractiu, igual que si la càrrega elèctrica q és negativa.
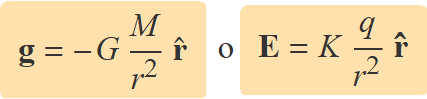
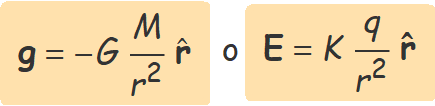
r = vector de la massa/càrrega al punt on es calcula el camp,
r = mòdul de r (correspon a la distància del punt a M o a q),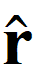 = r / r (vector unitari o de mòdul 1 paral·lel a r).
La direcció del camp gravitatori i del camp elèctric en un punt és radial des de la posició de M o de q, respectivament. Aquests camps es diuen camps centrals.
La intensitat del camp gravitatori i del camp elèctric en un punt depèn de r−2. Els camps centrals amb aquesta dependència es diuen camps newtonians.
Els dos camps cumpleixen el principi de superposició.
Una propietat dels camps centrals és que són conservatius. El treball del camp entre dos punts és independent del camí entre els dos punts. El treball es pot calcular a partir de la funció potencial.
El principi de conservació de l'energia s'escriu de manera semblant per als dos camps,
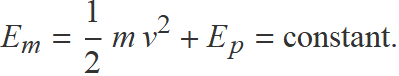
El terme de l'energia potencial depèn del camp. Per exemple:
Cas d'una partícula de massa m dins el camp gravitatori d'una massa M,
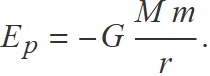
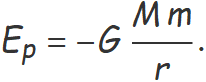
Partícula de massa m amb càrrega q dins el camp elèctric d'una càrrega Q,
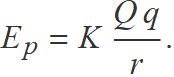
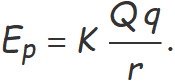
Les interaccions gravitatòria i elèctrica es descriuen bé amb expressions matemàtiques amb la mateixa forma dins un àmbit limitat de la física clàssica. El tractament físic més profund d'aquestes interaccions es diferent (i no entra en el temari d'aquest curs).
El tractament de la interacció gravitatòria i de la interacció elèctrica dins la física clàssica s'inicia amb partícules i càrregues puntuals i amb la mateixa forma matemàtica.
1
Sigui Fg la força d'atracció gravitatòria entre dues esferes d'10 kg amb els centres separats 1 m, i Fe la força d'atracció entre una partícula amb 1 nC i una amb −1 nC separades també 1 m.
a) És més gran Fg que Fe?
b) Què val Fg/Fe?
c) Quin hauria de ser el valor absolut de les càrregues de les partícules perquè la força d'atracció elèctrica fos igual que Fg?
2
a) Determina la força d'atracció gravitatòria màxima que es pot donar entre dues esferes d'or de 8 kg.
ρAu (densitat de l'or) = 19320 kg/m3,
volum esfera de radi R = 4 π R3 / 3.
b) Dues partícules amb càrregues iguals en valor absolut estan separades dues vegades el radi de les esferes. Quin és el valor absolut de la càrrega si la força d'atracció entre les partícules és igual que entre les esferes d'or?
Portada 
Temes 
Olimpíada