Camp gravitatori
La força d'atracció gravitatòria entre dues masses puntuals és proporcional a les masses i inversament proporcional al quadrat de la distància entres elles.
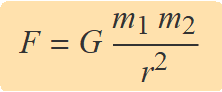
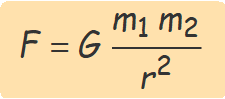
La força d'atracció gravitatòria entre dues esferes s'ha d'usar és proporcional a les masses i inversament proporcional al quadrat de la distància entres els centres de les esferes.
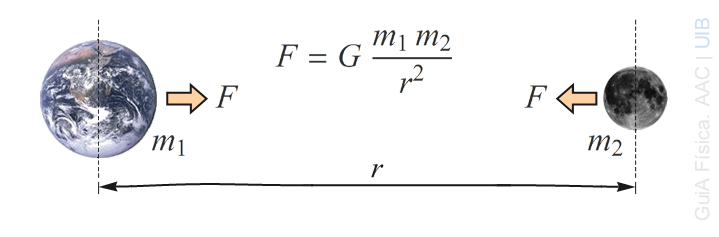
La constant de proporcionalitat per calcular l'atracció entre masses puntuals o esferes és la constant de gravitació universal que es determina experimentalment i té el símbol G.
G = 6.6743 10−11 N m2 kg−2
La constat G surt en el formulari:
Els planetes es consideraran esfèrics i els satèl·lits artificials, masses puntuals.
El principi de superposició estableix que la força gravitatòria total sobre un objecte de massa m a causa de diverses masses puntuals o esfèriques Mi és la suma vectorial de la força a causa per cada massa. En aquest cas, la força a causa de cada massa Mi s'ha de calcular amb
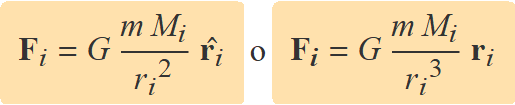
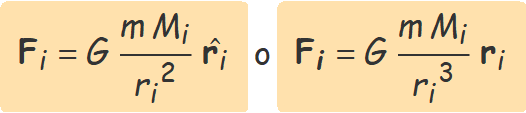
ri = vector que va del centre de masses de Mi al punt on es calcula el camp.
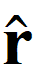i = ri/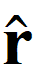i = vector unitari (que té mòdul 1) paral·lel a r.
En el cas de la força sobre m a causa de M1 i M2 s'ha de calcular
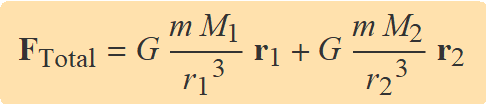
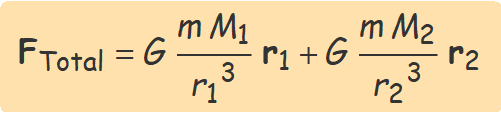
Tota massa crea un camp gravitatori.
El camp gravitatori d'una massa puntual m és radial i la seva intensitat a una distància r és
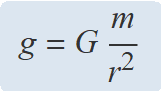
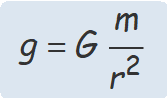
El camp gravitatori a l'exterior d'una massa esfèrica és com el d'una massa igual concentrada en el centre de l'esfera.
El principi de superposició estableix que el camp creat en un punt de l'espai a causa de diverses masses puntuals o esfèriques és la suma vectorial del camp creat per cada massa. En aquest cas, el camp de camp massa s'ha de calcular amb
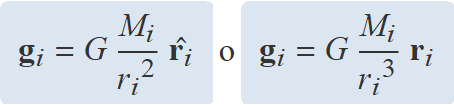
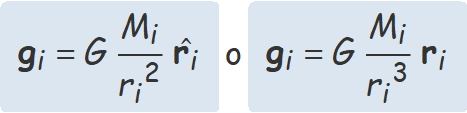
ri = vector que va del centre de masses de Mi al punt on es calcula el camp.
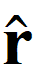i = ri/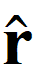i = vector unitari (que té mòdul 1) paral·lel a r.
El camp en un punt a causa de dues masses M1 i M2 és
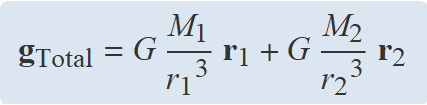
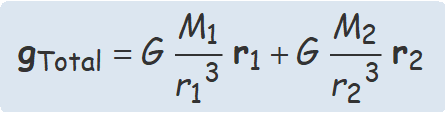
La Terra segueix una trajectòria el·líptica al voltant del Sol. El periheli és el punt de l'òrbita més proper al Sol i està a 147.1 106 km de l'estrella. L'afeli és el punt més llunyà i està a 152.1 106 km.
a) Què val la força del Sol sobre la Terra quan passa per l'afeli?
b) I quan passa pel periheli?
c) En quin tant per cent augmenta la força d'atracció del Sol sobre la Terra entre el pas de la Terra per l'afeli i el pas pel periheli?
MS (massa del Sol) = 1.989 × 1030 kg,
MT (massa de la Terra) = 5.972 × 1024 kg.
Resolució mostrar
Usant la distància Sol-Terra quan el planeta passa per l'afeli expressada en metres dins l'equació de la força d'atracció gravitatòria
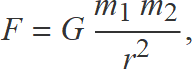
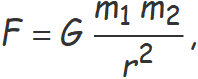
s'obté
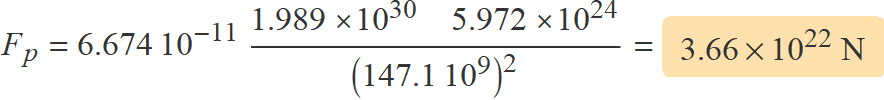
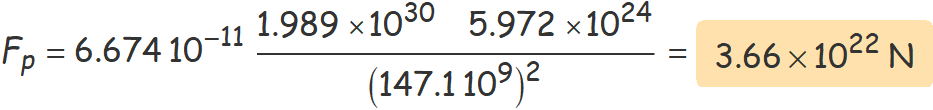
Usant la distància Sol-Terra quan el planeta passa pel periheli expressada en metres dins l'equació de la força d'atracció gravitatòria
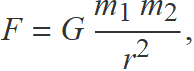
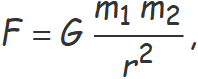
s'obté
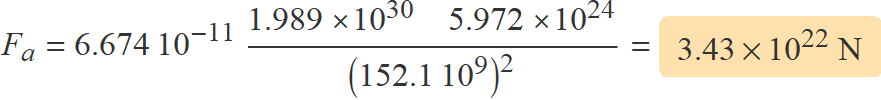
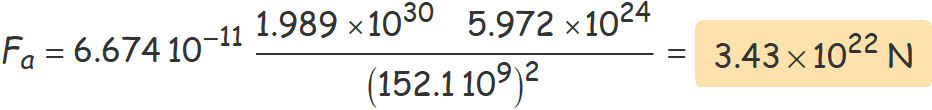
La variació en tant per cent entre la força d'atracció sobre la Terra quan passa per l'afeli i la força d'atracció quan passa pel periheli és
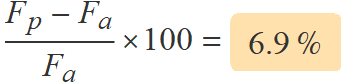
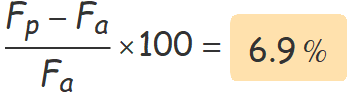
El perigeu de l'òrbita d'un satèl·lit al voltant de la Terra és el punt més proper de l'òrbita a la Terra. El punt més allunyat és el perigeu. La Lluna és un satèl·lit natural de la Terra i la seva distància al nostra planeta canvia al llarg del mes entre el perigeu i l'apogeu.
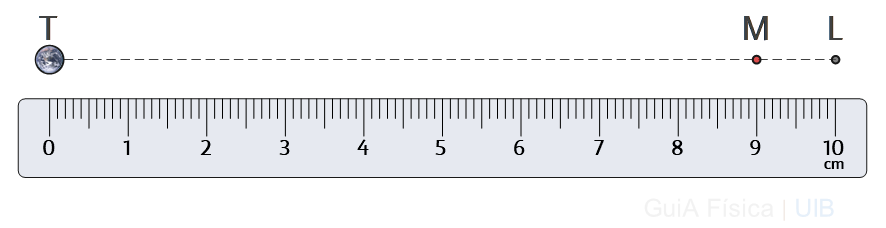
a) Considera el moment en que la Lluna passa pel perigeu i es troba a 359503 km del centre de la Terra. Calcula la distància al centre de la Lluna del punt intermedi M de la línia Terra-Lluna on l'atracció gravitatòria de la Lluna just supera l'atracció de la Terra.
b) Dibuixa un segment recte de 10 cm de longitud; un extrem representa el centre de la Terra i l'altre, el centre de la Lluna en el perigeu. Marca la posició del punt M sobre el segment.
c) Per respondre l'apartat a es planteja una equació de segon grau que té dues arrels. Una arrel és la solució demanada en el problema. Raona quin és el significat de l'altra arrel. Quines són les intensitats del camp gravitatori a causa de la Terra i de la Lluna associades a la segona arrel?
ML (massa de la Lluna) = 7.349 × 1022 kg.
MT (massa de la Terra) = 5.972 × 1024 kg.
Resolució ⊃ video mostrar
Si encara no has resolt el primer apartat, l'has de resoldre abans de llegir la resposta.
Resposta mostrar
Amb l'equació resultat d'igualar les forces d'atracció gravitatòria en un punt M de la línia recta entre els centres de la Terra i la Lluna, usant la distància x de M al centre de la Lluna, és una equació de segon grau que té una arrel positiva i una negativa.
L'arrel positiva localitza el punt M cercat entre la Terra i la Lluna.
L'arrel negativa localitza un punt N que està a la dreta de la Lluna segons la figura de l'apartat b. En aquesta altra punt, les atraccions gravitatòries de la Terra i de la Lluna també són iguals, però no es cancel·len perquè tenen el mateix sentit i se sumen.
A la figura següent es representen qualitativament les posicions dels dos punts respecte de la línia que passa pels centres de la Terra i la Lluna.
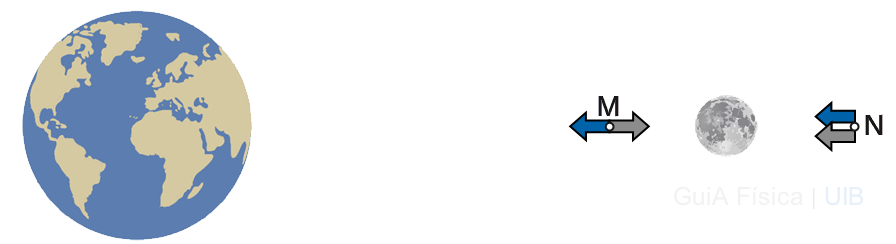
Saps perquè els punts M i N estan més a prop de la Lluna que de la Terra?
ocultarDetermina la força d'atracció gravitatòria màxima entre dues esferes de plom de 6 kg.
ρPb (densitat del plom) = 11.34 kg/m3,
volum esfera de radi R = 4 π R3 / 3.
Resolució mostrar
La força d'atracció gravitatòria màxima entre les dues esferes es donarà quan les esferes es toquin. Els centres estaran així a la mínima distància que serà 2R.
S'ha de determinar el radi a partir de la massa, la densitat i el volum,
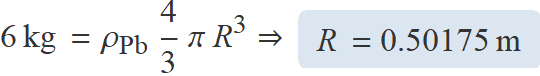
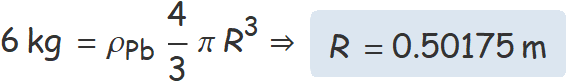
L'atracció gravitatòria entre les dues esferes quan els centres estiguin separats 2R és
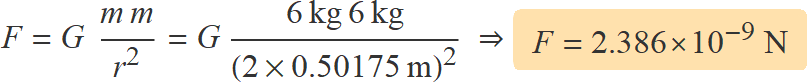
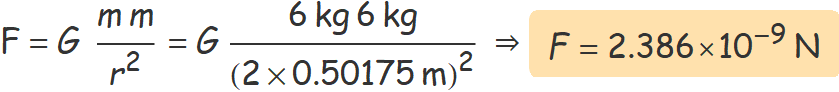
El camp gravitatori de dues masses és la suma vectorial dels camps de cada una de les masses. Quan les dues masses són iguals, els vectors camp són simètrics respecte a la mediatriu i al sumar-los queda un camp en la direcció de la mediatriu.
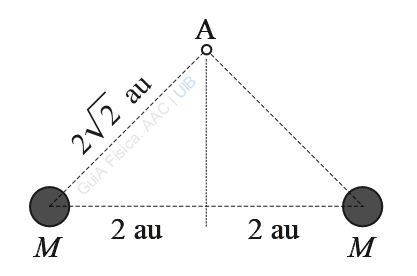
Es plantejarà el càlcul del camp en el punt A de la figura adjunta en el cas
M = 2.0 × 106 kg.
a) Dibuixa les fletxes que representen el camp en el punt A. Fes la suma gràfica per trobar la direcció i el sentit del camp total.
b) Calcula el mòdul del camp total en el punt A.
Resolució mostrar
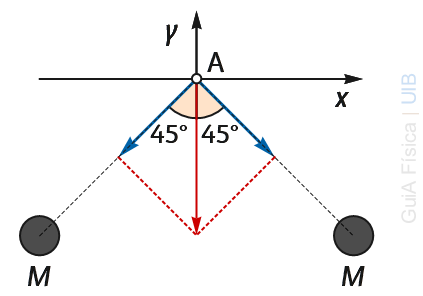
A la figura, s'han dibuixat eixos de coordenades cartesianes amb origen en el punt A. Els dos vectors camp dibuixats de color blau tenen la mateixa longitud i formen el mateix angle de 45° amb la vertical. La suma gràfica dels vectors dona un vector vertical cap a baix, perpendicular a la línia entre les dues masses.
S'usarà
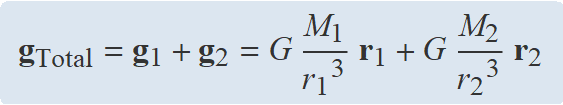
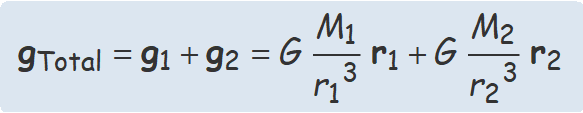
• Càlcul del camp g1
Aquest és el camp de la massa esquerra en el punt A.
M1 = 2 × 106 kg,
distància de la massa esquerra a A = 2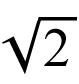 
au ≈ 4.2313 × 1011 m,
vector r de la massa esquerra a A = (2, 2) au,
vector unitari 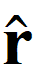de M a A = (1, 1).
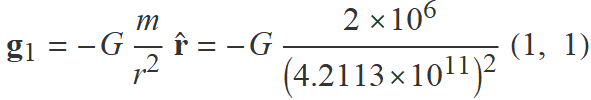
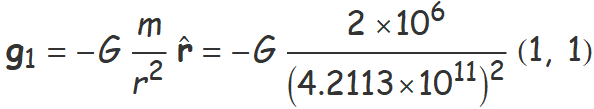
g1 = (−5.272, −5.272) × 10−28 N/kg
• Càlcul del camp g2
Aquest és el camp de la massa dreta en el punt A.
La massa dreta és la mateixa que la massa esquerra i la distància al punt A, també. Només canvia la direcció i el sentit del camp. Usant el resultat de l'apartat anterior es pot escriure, sense haver de repetir els càlculs,
g2 = (5.272, −5.272) × 10−28 N/kg
• Càlcul del camp total gT en el punt A
gT = g1 + g2 = (0, −10.544) × 10−28 N/kg
El mòdul del camp és el valor absolut de la segona component
gT = 10.544 × 10−28 N/kg
Com que el camp total és vertical, el mòdul és la suma de les components verticals dels dos camps. Les components verticals són iguals,
g1,y = g2,y = ge cos(45°).
Per tant,
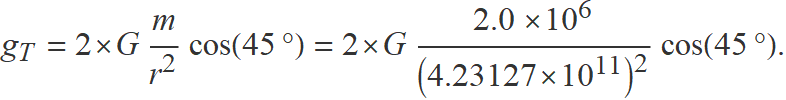
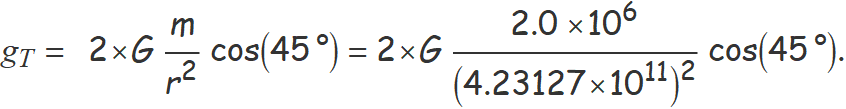
El resultat és el que ja s'ha obtingut.
ocultar
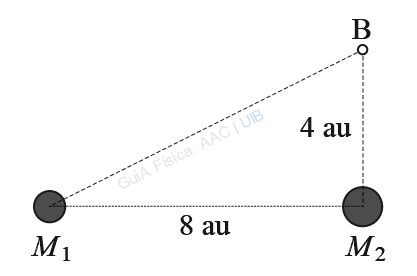
Es plantejarà el càlcul del camp en el punt B de la figura adjunta en el cas
M1 = 1.6 × 106 kg,
M2 = 2.0 × 106 kg.
La línia B−M2 és perpendicular al segment M1−M2.
a) Dibuixa les fletxes que representen el camp en el punt B. Fes la suma gràfica per trobar la direcció i el sentit del camp total.
b) Calcula el mòdul del camp total en el punt B.
c) Si en el punt B hi ha una massa de 104 kg, quin és el mòdul de la força gravitatòria total?
Resolució mostrar
A la figura, s'han dibuixat eixos de coordenades cartesianes amb origen en el punt B. El vector que representa el camp en el punt B a causa de M1 té menys longitud que el vector que representa el camp a causa de M2 perquè la massa M1 és menor que M2 i el punt B està més enfora de M1 que de M2.
S'usarà que
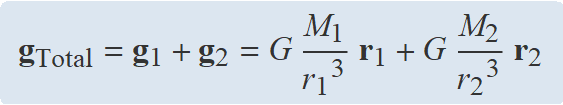
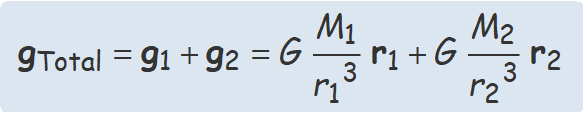
• Càlcul del camp g1
Aquest és el camp de la massa M1 en el punt B.
M1 = 1.6 × 106 kg,
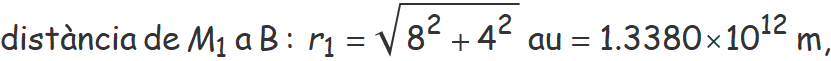
vector r1 de M1 a B: (8, 4) au,
vector unitari 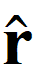1 de M1 a B = r1/r1
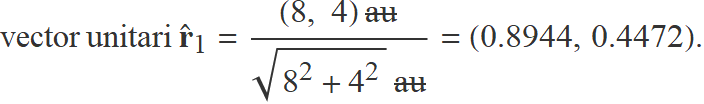
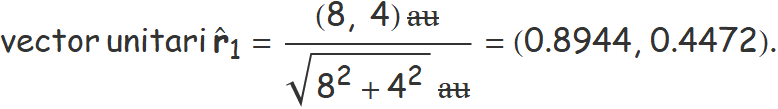
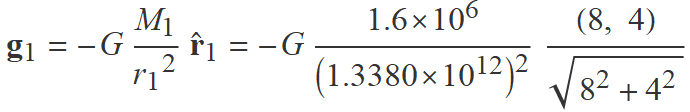
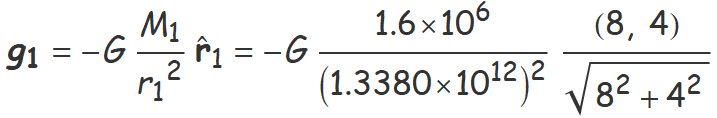
g1 = (−5.3349, −2.6675) × 10−29 N/kg
• Càlcul del camp g2
Aquest és el camp de la massa M2 en el punt B.
M2 = 2.0 × 106 kg,
distància de M2 a B: r2 = 4 ua = 5.9839×1012 m,
vector r2 de M2 a B: (0, 4) ua,
vector unitari 2 de M2 a B = r2/r2 = (0, 1) (directament!)
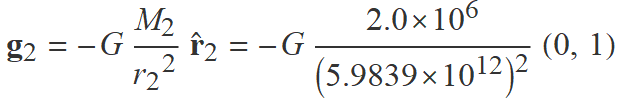
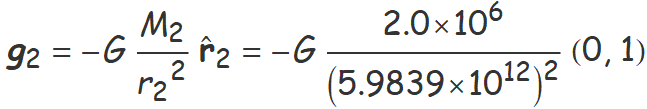
g2 = (0, −37.279) × 10−29 N/kg
• Càlcul del camp total en el punt B
El mòdul del camp total en el punt B es determina calculant primer el vector camp total
gT = g1 + g2 = (−5.3349, −39.946) × 10−29 N/kg
Llavors,
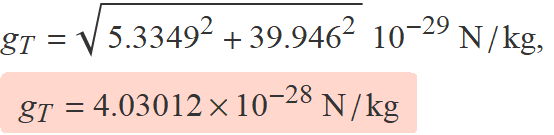
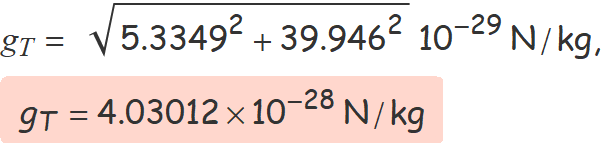
La força gravitatòria sobre una massa 104 kg en el punt B és
F = 104 kg × ET = 104 kg × 4.03012 × 1028 N/kg,
F = 4.030 × 10−24 N
Isaac Newton publicà la llei de la gravitació universal el 5 de juliol de 1687. Un dels grans èxits que tingué va ser explicar les lleis de Kepler del moviment planetari. Lleis que s'estudiaran en una pàgina d'aquest mateix bloc.
Per als problemes següents es necessitarà el valor de la constant de gravitació universal que surt en el formulari,
G = 6.6743 10−11 N m2 kg−2.
1
El radi mitjà i la massa de la Terra són
RT = 6371.0 km,
MT = 5.9722 × 1024 kg.
L'atracció gravitatòria de la Terra sobre un objecte de massa M a la superfície és
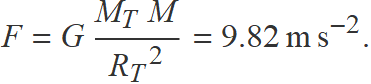
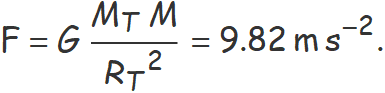
Calcula a quina altura sobre la Terra la força d'atracció sobre l'objecte s'haurà reduït a la meitat.
2
Es volen comparar les forces d'atracció gravitatòria del Sol i de la Terra sobre la Lluna. Com que les distàncies canvien al llarg de l'any, es farà una comparació aproximada. Es calcularà el quocient de la força FS−L del Sol sobre la Lluna dividida per la força FT−L de la Terra sobre la Lluna quan la Lluna està a una distancia donada del nostre planeta.
La massa de la Lluna i la distància Sol-Lluna no es donaran. Per què aquestes dues dades no són necessàries per a la comparació demanada?
MS (massa del Sol) = 1.9891 × 1030 kg,
MT (massa de la Terra) = 5.9722 × 1024 kg,
distància mitjana Sol-Terra = 1 au ≈ 149.6 × 109 m.
distància mitjana Terra-Lluna = 384400 km.
Els planetes no són perfectament esfèrics ni tenen la massa distribuïda de manera uniforme, però suposar-ho i negligir la rotació permet obtenir una estimació de l'acceleració de la gravetat amb la llei de gravitació universal.
3
Calcula una estimació de l'acceleració de la gravetat a la superfície de Mart en el seu equador suposant que el planeta és esfèric i la massa està distribuïda uniformement.
Mm (massa de Mart) = 6.4171 × 1023 kg,
Rm (radi equatorial de Mart) = 3396.2 km.
4
Fes una estimació de la massa de la Lluna usant el radi mitjà (1737.4 km) i l'acceleració de la gravetat superficial (1.622 m/s−2).
5
L'acceleració de la gravetat a la superfície terrestre és g. Si a la superfície d'un planeta amb el doble de massa que la Terra i el doble de radi l'acceleració és gp, què val g/gp?
6
a) A la Lluna, a quina altura s’ha reduït l’acceleració de la gravetat a la meitat del valor que té a la superfície?
b) Quin radi hauria de tenir la Lluna perquè l’acceleració de la gravetat superficial fos igual que l’acceleració de la gravetat a la superfície de la Terra?
Imatge de la Lluna.Missió LRO (NASA)
RL (radi mitjà de la Lluna) = 1737.4 km,
ML (massa de la Lluna) = 7.3477 × 1022 kg,
RT (radi mitjà de la Terra) = 6371.0 km,
MT (massa de la Terra) = 5.9722 × 1024 kg.
Les contribucions més importants al camp gravitatori en el que es mouen anualment els satèl·lits de Júpiter són la de Júpiter i la del Sol. El camps del planeta i del Sol s'han de sumar vectorialment. Es treballa la suma de dos camps gravitatoris en els problemes següents.
7
Una estrella S amb la mateixa massa del Sol té un sistema planetari. En un moment donat, les posicions del l'estrella S, el planeta J (semblant en massa a Júpiter) i el planeta P més petit són els vèrtex d'un triangle rectangle com mostra la figura adjunta.
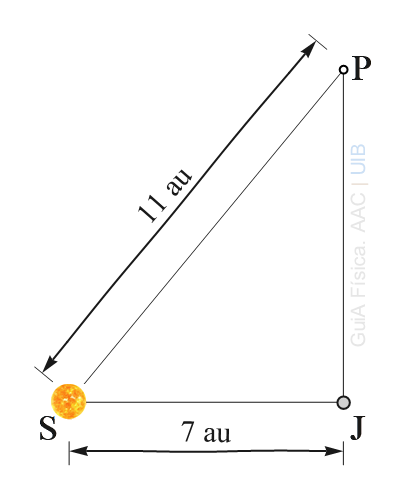
a) Copia el triangle rectangle i dibuixa les fletxes que representen les forces d'atracció gravitatòria de S sobre P i de J sobre P. Dibuixa també la suma gràfica d'aquestes dues forces.
b) Calcula la intensitat de la força gravitatòria total sobre P a causa de S i J. Recorda que les forces s'han de calcular en forma vectorial, sumar les components vectorialment perquè les forces no tenen la mateixa direcció i, després, calcular el mòdul del vector suma.
1 au = 149597870700 m ≈ 149.6 × 109 m,
MS = 2.0 1030 kg,
MJ = 2.0 1027 kg,
MP = 7.0 1024 kg.
7.a)
Les fletxes negres de la figura adjunta representen les forces atractives de S i P sobre J. La fletxa vermella representa la suma de les dues forces obtinguda fent la suma gràfica amb el paral·lelogram format per les fletxes negres i les línies de punts.
8
Dos satèl·lits iguals segueixen la mateixa òrbita al voltant de la Terra i mantenen una distància fixa. Es vol calcular la força que fan els dos satèl·lits sobre un tercer satèl·lit que es troba a 7 km de cada un.
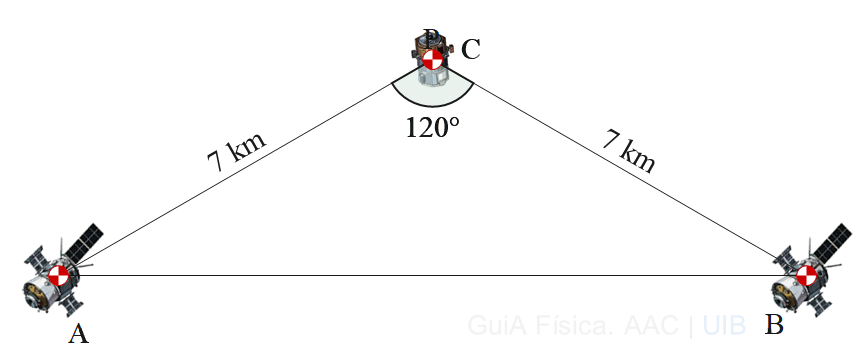
MA = 1500 kg,
MB = 1500 kg,
MC = 590 kg.
La distancia entre els satèl·lits es bastant gran comparada amb la seva mida. Per això, es pot suposar que tota la massa dels satèl·lits està en en el centre de masses i usar l'expressió de la força d'atracció entre esferes o masses puntuals.
a) Dibuixa un diagrama de les forces sobre el satèl·lit C i mostra que la suma de les forces dona una força total perpendicular a la línia A-B.
b) Mostra gràficament que la component de la força FBC de B sobre C en la direcció vertical del dibuix és FBC cos(60°) on FBC és el mòdul de la força FBC.
c) Calcula la força total dels satèl·lits A i B sobre el satèl·lit C.
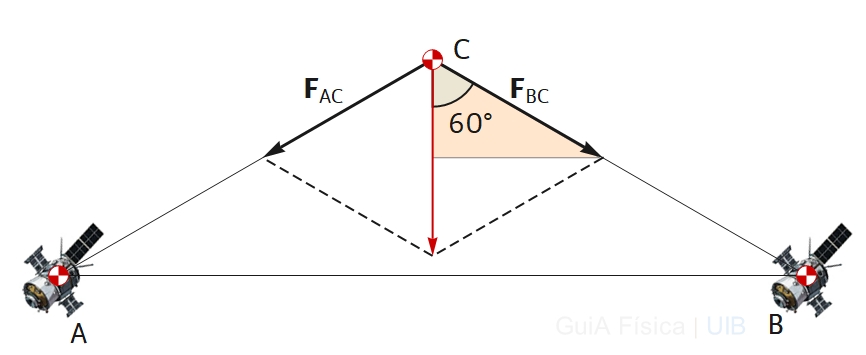
8.a)
Les fletxes negres de la figura adjunta representen les forces atractives d'A i B sobre C. La fletxa vermella representa la suma de les dues forces obtinguda fent la suma gràfica amb el paral·lelogram format per les fletxes negres i les línies discontinues. La força total té la direcció perpendicular al segment A-B.
8.b)
La component vertical de la força FBC és FBC cos(60°) (el triangle taronja s'ha dibuixat com a referència d'aquest valor).
La força d'A sobre C té la mateixa component vertical. Llavors, la força suma d'A i B sobre C es pot calcular com la suma de les dues components verticals:
FT = 2 FBC cos(60°).
9
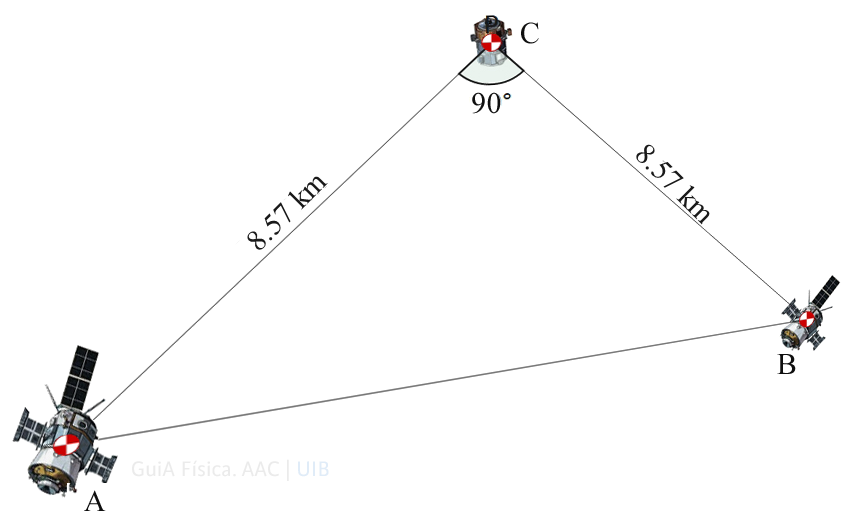
Calcula la força que fan els dos satèl·lits de l'exercici anterior sobre el tercer quan aquest es troba a 8.57 km de cada un.
10
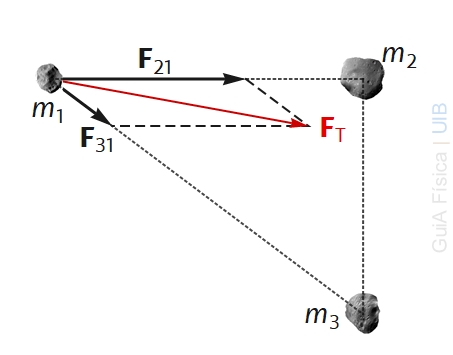
La figura representa les posicions en un moment donat de tres asteroides. Les masses m1, m2 i m3 dels asteroides s'indiquen a la figura. Calcula el mòdul de la força sobre el primer asteroide a causa de:
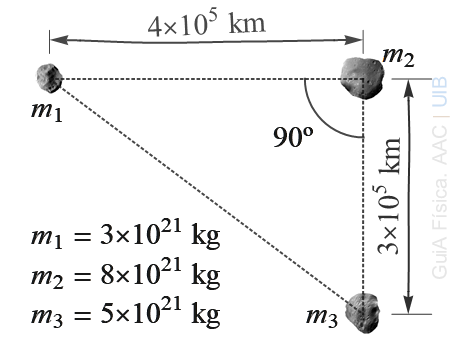
a) El segon asteroide.
b) El tercer asteroide.
c) El segon i el tercer asteroide en conjunt.
d) Dibuixa el triangle de línies discontínues de la figura amb el vector que representa qualitativament la força total sobre el primer asteroide. (La solució es mostrarà quan els apartats anteriors s'hagin respost correctament.)
10.d) La fletxa vermella de la figura representa la força total sobre l'asteroide de massa m1. Les fletxes negres representen els forces individuals dels asteroides 2 i 3 sobre el primer.
Portada 
Temes 
Olimpíada