
Òptica


L'índex de refracció n d'un medi transparent és el quocient entre la velocitat de la llum en el buit i la velocitat de la llum en el medi,
n = c / v.
Per a la llum visible, l'índex de refracció dels medis transparents és superior a 1 i sol ser inferior a 2. Una excepció és el diamant que té un índex de refracció més alt.
El valor de l'índex de refracció depèn de la longitud d'ona de la llum i, per tant, si un raig de llum blanca es refracta, es produeix el fenòmen de la dispersió.

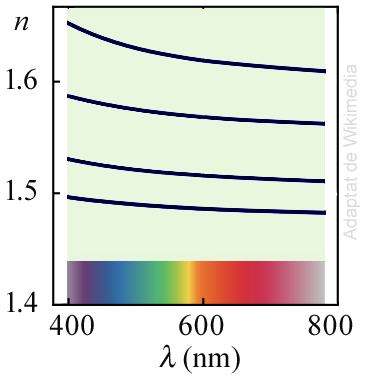
Per a la llum visible, els índexs de refracció de vidres transparents decreix amb la longitud d'ona com mostra la figura per a quatre tipus de vidres.
Els valors de cada vidre s'ajusten a la funció n(λ) = A + B / λ2. L'índex de refracció d'un medi per a la llum vermella (λ ≈ 700 nm) és més baix que per a la llum violeta (λ ≈ 400 nm).
L'índex de refracció de l'aire és 1,00029, i per tant, es pren en els exercicis igual a 1.

La línia perpendicular a la superfície de separació entre dos medis en el punt d'incidència d'un raig es diu normal en el punt d'incidència.

El raig incident, la normal en el punt d'incidència i el raig refractat estan dins un pla, anomenat pla d'incidència.

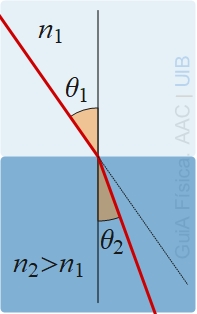
La llei de Snell estableix que
n1 sin(θ1) = n2 sin(θ2),
on
n1: índex de refracció del medi per on ve el raig,
n2: índex de refracció del medi per on surt el raig refractat,
θ1: angle d'íncidència
θ2: angle de refracció
Els angles θ1 i θ2 es mesuren des de la normal cap el raig incident i refractat, respectivament.
Donats n1, θ1 i n2 es pot calcular l'angle θ2 amb la funció arcsinus:
θ2 = arcsin(n1 sin(θ1) / n2)

Quan la llum incideix sobre la superfície que separa dos medis d'índex de refracció diferents, part de la llum es reflecteix i l'altra part es trasmet al segon medi. La quantitat de llum que es reflecteix depèn de l'angle d'incidència.
Quan n2 < n1 (per exemple quan la llum ver per dins aigua cap a la superficie que la separa de l'aire), la llei de Snell només té solució sí
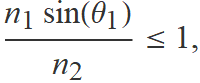
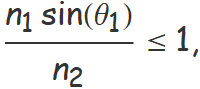
ja que l'argument de la funció arcsinus ha de ser inferior o igual a 1. Aïllant θ1, s'obté
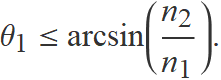

Això significa que, quan n2 < n1, la llum només es refracta sí l'angle d'incidència és menor que l'angle límit

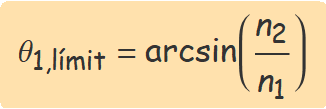
Quan la llum incideix des d'un medi amb un índex de refracció més alt que el segon medi i un angle θ1 > θ1,límit, no hi ha llum refractada, tota la llum es reflecteix i es diu que hi ha reflexió total.
Quan l'angle d'incidència creix i s'acosta θ1,límit, la intensitat de la llum refractada va disminuint i es fa zero quan l'angle d'incidència iguala o supera θ1,límit.


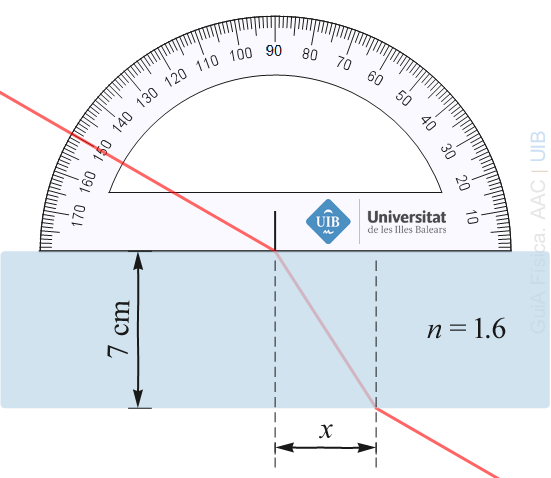
Un raig de llum travessa una làmina d'un material transparent com mostra la figura. L'índex de refracció de material és 1.6.
a) Què val x?
b) És el raig a la sortida de la làmina paral·lel a la direcció inicial del raig o només ho pareix en el dibuix?
Resolució mostrar

L'angle d'íncidència mesurat sobre el porta angles és θ1 = 60°.
L'angle de refracció es determina amb la llei de Snell:
sin(60°) = 1.6 sin(θ2) ⇒ θ2 = 32.77°.
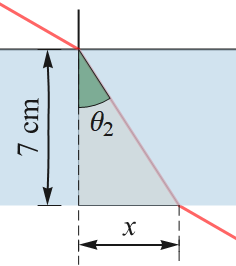
L'angle de refracció és l'angle que forma el raig dins la làmina amb la línia discontinua vertical, de manera que la tangent de l'angle θ2 també és (veure figura),
tan(θ2) = x / 7 ⇒ x = 4.51 cm

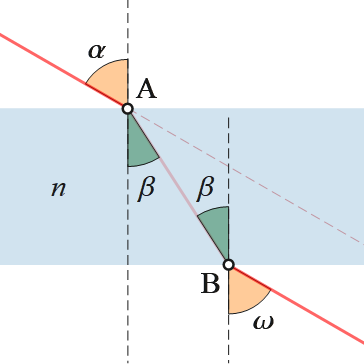
El raig es refracta primer en el punt A, des de l'aire cap al medi d'índex de refracció n i després en el punt B, des d'aquest medi cap a l'aire. Per la igualtat d'angles interns d'una secant de dues rectes paral·leles, l'angle de refracció en el punt A és igual que l'angle d'incidència en el punt B.
La llei de Snell s'aplica en el punt A amb els angles θ1 = α i θ2 = β:
sin(α) = n sin(β)
La llei de Snell s'aplica en el punt B amb els angles θ1 = β i θ2 = ω:
n sin(β) = sin(ω)
De les dues equacions, donen
sin(ω) = sin(α) ⇒ ω = α
L'angle del raig de sortida amb la normal és el mateix que formava el raig inicial amb la normal. Per tant,
El raig a la sortida de la làmina és paral·lel a la direcció inicial del raig
ocultar
Un raig de llum travessa una làmina de vidre d’índex de refracció 1,47 i 5 cm de gruix. El raig segueix inicialment la línia L que mostra la figura. L’angle d’incidència del raig es mesura amb l’escala marcada en graus.
a) Què val x en el cas de la figura?

b) Dibuixa la línia L i la trajectòria del raig quan surt del vidre de manera qualitativament correcta. Travessa el raig en sortir del vidre la línia L? Justifica la resposta breument.
c) Calcula la distància x.
d) Hi ha algun angle d’incidència per al qual x té un valor màxim? Si n’hi ha algun, calcula aquest valor màxim. Si no, indica per què no hi ha màxim?
Resolució mostrar

L'angle del raig amb la línia horitzontal (perpendicular a la superfície de la làmina) és de 40°. Llavors,
sin(40°) = 1.47 sin(θk) ⇒ θk = 25.93°

La direcció que segueix un raig després de trevessar una làmina de cares plano paral·leles és paral·lela a la direcció inicial del raig. El raig a la sortida s'ha de dibuixar paral·lel a la línia discontinua L
El raig a la sortida és paral·lel a L. Per tant, no travessa la línia L.

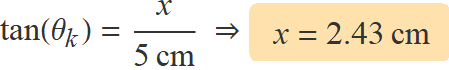
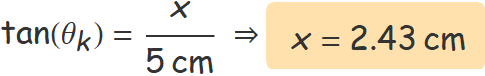

La perpendicular a les cares de la làmina és la línia horitzontal a la figura. L'angle que forma el el raig amb aquesta línia és més gran, i per tant x es més, com més gran és l'angle d'incidència, el qual pot arribar a 90°. Així:
sin(90°) = 1.47 sin(θmàx) ⇒ θmàx = 42.86°
El valor màxim de x és
xmàx = 5 cm tan(θmàx) ⇒ xmàx = 4.64 cm
ocultar
La figura representa la trajectòria d'un raig quan travessa dos prismes de base semicircular. El raig incideix primer en el prisma gran. Els radis de les bases son 4 cm i 2.9 cm.
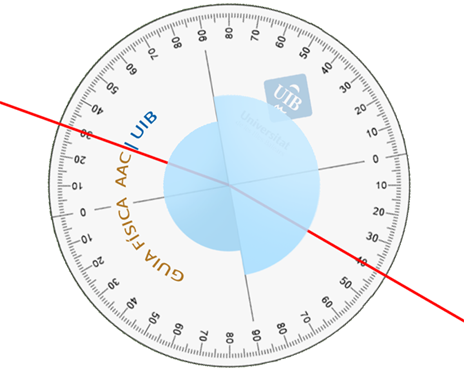
a) Determina els angles d'incidència i refracció del raig a la superfície plana de contacte dels dos prismes.
b) Es pot determinar el valor dels índexs de refracció dels prismes? Si es pot, determina'ls; si no, què es pot afirmar sobre els índexs?
c) Si el prisma gran tingués un índex de refracció 1.45, quan de temps tarda la llum en creuar els dos prismes?
Resolució mostrar

Cal remarcar que la normal a la superficie és la línia entre les marques de zero graus a l'esquerra i la dreta. Els prismes s'han col·locat sobre la base graduada perquè les marques de graduació donin directament els angles d'incidència i de refracció.
L'enunciat indica que el raig incideix primer en el prisma gran, per tant, a la figura el raig va de la dreta cap a l'esquerra. Els angles d'íncidència i de refracció a la superfície de contacte dels prismes són
θ1 = 40°,
θ2 = 30°.

Sigui n1 l'índex de refracció del prisma gran i n2 el del prisma petit. D'acord amb la llei de Snell,
n1 sin(40°) = n2 sin(30°) ⇒ n1 / n2 = 0.778
Els valors dels índex de refracció no es poden determinar.
Es pot afirmar que n1 < n2 i quin és el quocient n1 / n2.

El temps que tarda la llum en trevessar els dos prismes és
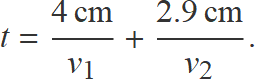
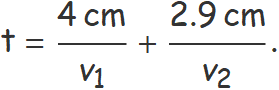
La velocitat de la llum dins cada medi és vi = c / ni.
Si n1 = 1.45, llavors n2 = 1.86.
Usant la velocitat de la llum, s'obté
t = 0.374 ns
ocultar
La figura representa la trajectòria d’un raig de llum que travessa un vidre, una capa d’aigua i surt a l’aire. Uns 1.33 per a l'índex de refracció de l'aigua.
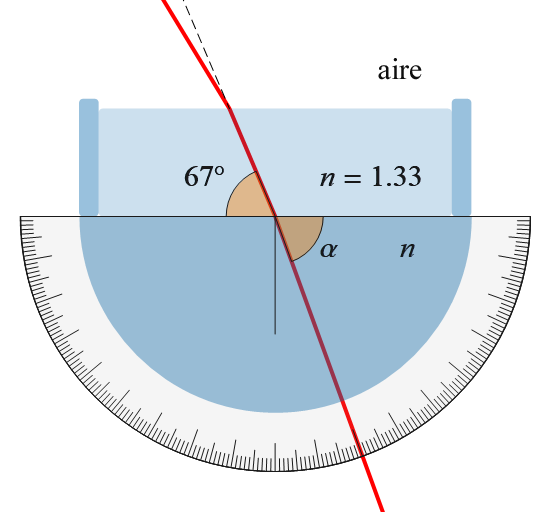
a) Dibuixa qualitativament la trajectòria del raig quan surt a l’aire des de
l’aigua.
b) Calcula l’índex de refracció del vidre. La direcció del raig dins el vidre es mesura amb l’angle α sobre l’escala graduada.
c) Es canvia el vidre per un altre d’índex de refracció 1.55. Calcula el valor
de l’angle α a partir del qual el raig no passa de l’aigua a l’aire.
Resolució mostrar

Atès que l'índex de refracció de l'aire és inferior al de l'aigua, el raig s'allunya de la normal.


L'angle α és de 70° d'acord amb el cercle graduat.
Els angles d'incidència i refracció es mesuren des de la normal. Per tant,
θ1 = 90° − 67° = 23°,
θ2 = 90° − α = 20°
La llei de Snell amb aquests angles és
1.33 sin(23°) = n sin(20°) ⇒ n = 1.52

El raig no passa de l'aigua a l'aire si incideix amb un angle igual o superior a l'angle límit entre l'aigua i l'aire.
Per a l'angle d'incidència igual a l'angle límit θlím, el raig refractat formaria 90° amb la normal.
1.33 sin(θlím) = 1 sin(90°) ⇒ θlím = 48.75°
L'angle d'incidència del raig a la superfície aigua-aire és igual que l'angle amb que es refracta el raig a la superfície vidre-aigua. La llei de Snell permet calcular l'angle amb que ha d'incidir el raig en aquesta superfície. Com que es demana l'angle α i no l'angle amb la normal,
1.55 sin(90° − α) = 1.33 sin(48.75°) ⇒ α = 49.82°
ocultar
Tres líquids immiscibles tenen la mateixa densitat i són de color rosat, blau i verd. Els índexs de refracció dels líquids son 1.57, 1.54 i 1.52, respectivament. S'agafen sis vasos i s'omplen de manera diferent amb un líquid en el fons i un altre damunt

Si un raig de llum arriba a la superfície entre els dos líquids pel líquid de baix, en quins casos hi podria haver reflexió total? Quin és l'angle límit més petit?
Resolució mostrar
Quan hi ha reflexió total a la superficie entre dos medis, el medi per on viatge el raig té un índex de refracció més alt que l'índex de l'altre medi.
Tenint en compte que
nvermell > nblau > nverd,
i que el raig entra per dalt, el líquid de baix del vas té l'índex de refracció més alt que el del líquid de dalt en els casos:
2, 4 i 6

Els angles límit són (arrodonits a dos decimals per baix),
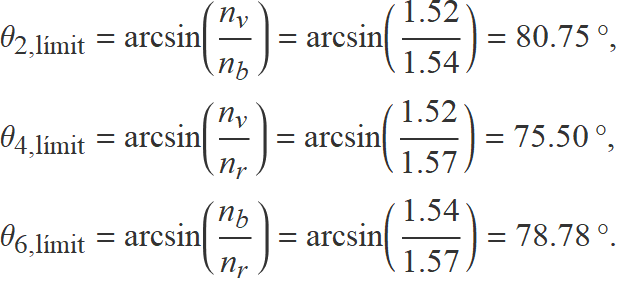
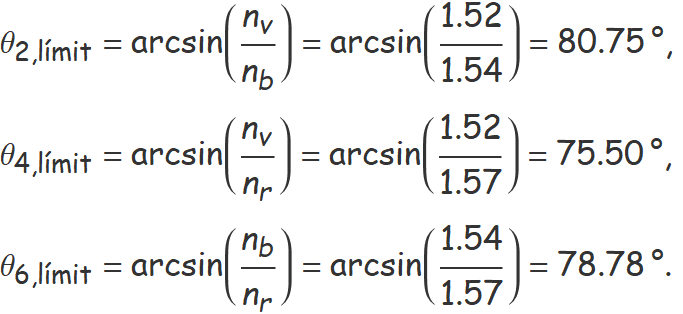
L'angle límit més petit dels tres és
θ4,límit = 75.70°
ocultar
El raig d’un làser es dirigeix cap a un bloc de plàstic de secció rectangular i índex de refracció nv = 1.4. El raig es dirigeix en una direcció A i, després, en una altra direcció B. Les dues direccions s’han representat a la figura. Usa el porta angles per determinar l’angle d’incidència del raig sobre el bloc en cada cas.
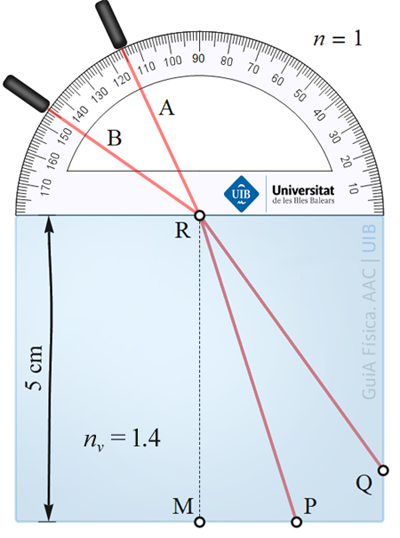
a) Quan el raig ha seguit la direcció A dins l’aire, passa per un punt P de la cara inferior del bloc, a la dreta del punt M de la vertical del punt de refracció. Calcula la distància entre els punts M i P.
b) Quant de temps tarda la llum per avançar 3 cm al llarg del segment R-P?
c) Quan el raig ha seguit la direcció B dins l’aire, arriba al punt Q de la cara dreta del bloc. Determina si el raig es reflecteix totalment o no en aquest punt
Resolució mostrar

L'angle del raig RP i la normal RM en el punt R es pot calcular amb la llei de Snell. L'angle del raig A amb la normal és (mesurat amb el porta angles) de 25°. Llavors,
sin(25°) = 1.4 sin(θa) ⇒ θa = 17.57°.
La tangent d'aquest angle és la distància MP dividia per 5 cm, de manera que
dMP = 5 cm tan(17.57°) ⇒ dMP = 1.58 cm

La velocitat de la llum dins el plàstic és v = c − / n. Així,
t = 3 cm / v ⇒ t = 0.14 ns

L'angle d'incidència del raig B en el punt R és de 55°. La llei de Snell proporciona l'angle de refracció,
sin(55°) = 1.4 sin(θb) ⇒ θb = 35.81°.
L'angle d'incidència del raig en el punt Q és
90° − 35.81° = 54.19°.
L'angle límit entre el plàstic i l'aire,
θlím = arcsin(1 / 1.4) = 45.58°.
L'angle d'incidència és més gran que l'angle límit. En conseqüència:
El raig es reflecteix totalment en el punt Q
ocultar
La llei coneguda pel nom de Willebrord Snellius relaciona les direccions de la llum quan passa d'un medi a un altre, i es quantifica usant l'índex de refracció del medi.

1
La llum monocromàtica de 500 nm és de color verd. Dins el diamant es propaga a 124000 km/s. Què val l'índex de refracció del diamant per a aquest color?
2
Un raig de llum làser es dirigeix des de l'interior d'un recipient amb aigua de mar cap a la superfície. El raig s'allunya de la normal quan surt de l'aigua com mostra l'animació.

Quin és l'índex de refracció de l'aigua de mar si el raig dins i fora de l'aigua forma angles de 23.0º i 32.1º amb la vertical?
3
A l'examen de les proves d'accés, el resultat d'un apartat no és normalment necessari per respondre els apartats següents, però en aquesta qüestió sí que es necessari el resultat de la pregunta anterior. Quin és l'angle del raig amb la vertical dins l'aigua de mar en el recipient de la pregunta anterior quan el raig surt formant un angle de 45º?

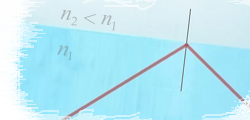
La llum no es refracta a partir de cert angle d'incidència cap a un medi menys dens (d'aigua a aire, per exemple). Una aplicació del fenomen és la conducció de llum làser per l'interior d'un tipus de fibra òptica.

4
L'índex de refracció dels medis transparents depèn de la longitud d'ona. Per exemple, l'aigua té un índex de refracció que va de 1.340 per a la llum monocromàtica blava fins a 1.331 per a la llum monocromàtica vermella. Calcula l'angle límit per a una refracció des de l'aigua a l'aire de la llum blava i de la llum vermella.
5
Tenim tres líquids immiscibles de la mateixa densitat i de colors rosat, blau i verd. Els índexs de refracció dels líquids son 1.53, 1.51 i 1.56. S'agafen sis vasos i s'omplen de manera diferent amb un líquid en el fons i un altre damunt

Si un raig de llum arriba a la superfície entre els dos líquids pel líquid de dalt, en quins casos hi podria haver reflexió total? Quin és l'angle límit més petit?
6
Una peça de vidre d'índex de refracció 1.621 té dues cavitats que contenen dos líquids. Els índexs de refracció dels líquids són 1.492 i 1.379. Dos raigs arriben a la part de baix de les cavitats amb el mateix angle d'incidència.
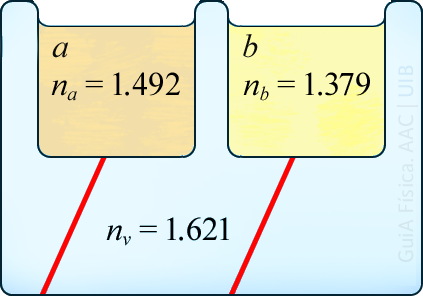
Quan s'augmenta per igual l'angle d'incidència dels dos raigs, un es reflecteix totalment primer i, per a un angle més gran, també es reflecteix totalment l'altre. Quin és l'angle d'incidència a partir del qual els dos raigs es reflecteixen totalment?
7
Tres làmines transparents d'índex de refracció 1.79, 1.51 i. 1.19 estan una damunt l'altra.
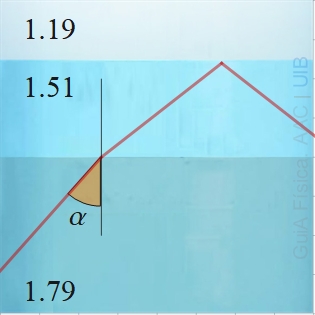
Què val l'angle α si és l'angle d'incidència més petit possible perquè el raig es reflecteixi totalment a la interfície entre els dos medis de dalt?
8
L'índex de refracció del vidre d'una fibra cilíndrica de diàmetre g = 1.5 mm és 1.56. La figura representa el raig que té la distància més curta possible entre reflexions totals.
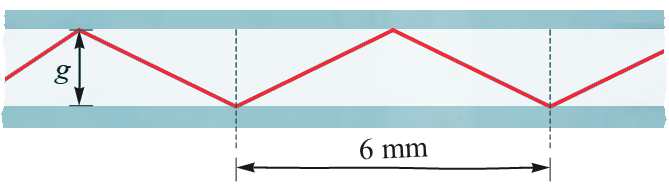
Quin és l'índex de refracció del medi que envolta la fibra?
