
Òptica
La llei de Snell relaciona la direcció de la llum abans i després de trevessar una superfície entre dos medis transparents. S'escriu en la forma
n1 sin(θ1) = n2 sin(θ2),
però amb una prisma transparent, només es pot fer verificar que
sin(θ2)/sin(θ1)
és constant.
Willebrord Snel van Royen va publicar la llei que es coneix amb la simplificació el seu llinatge en llatí, Snellius, a l'any 1621.
Un prisma transparent té la base en forma de semicercle i es col·loca sobre una plataforma circular giratòria de manera que el centre de curvatura de la base del prisma concideixi amb l'eix de gir de la plataforma (Fig. 1). La plataforma té marques de graduació per mesurar la direcció d'un raig procedent d'un làser abans i després de trevessar el prisma.
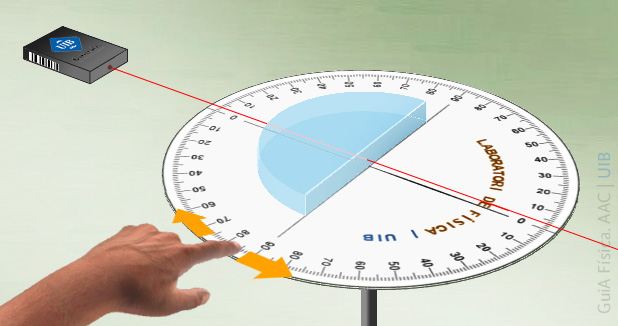

Posa el cursor sobre el disc graduat del gràfic (o dins la figura per tenir un poc més de resolució en el gir).
Pitja i manté el botó esquerra del ratolí i arrossega el cursor per girar el disc.
El làser està a l'esquerra fora del dibuix i crea el raig horitzontal.


El raig que arriba al prisma per la cara circular entra dins els prisma sense canviar de direcció com quan incideix perpendicularment sobre la cara plana. Aquesta observació es pot ampliar amb altres superfícies i es conclou que:
Un raig que incideixi sobre una superfície en direcció perpendicular al pla tangent a la superfície en el punt d'incidència, no canvia de direcció


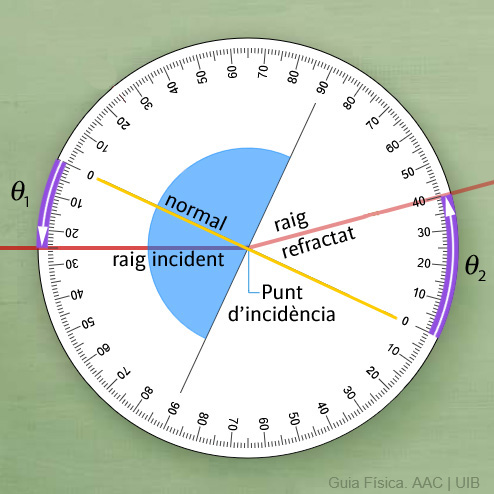
La direcció del raig abans i després de trevessar la superfície entre dos medis es mesura amb els angles θ1 i θ2 que forma el raig amb la normal en el punt d'incidència dins cada medi. (La normal és la línia perpendicular a la superfície.)
Els angles θ1 i θ2 es mesuren des de la normal en el mateix sentit: horari o antihorari. A la figura, els dos angles es mesuren en sentit antihorari (θ1 = 25° i θ2 = 40°). Si a la figura, el raig incident arribés per la part de dalt de la normal, els dos angles es mesurarien en sentit horari.
Si s'ha canviat el prisma amb el botó que apareix en un altre apartat, pulsa el botó següent per establir el prisma inicial.
Prepara una taula com la següent.
| θ1 | θ2 | sin(θ2)/sin(θ1) |
| 20° | ||
| 25° | 40° | |
| 30° | ||
| 35° | ||
| 40° |
Usa el cursor per girar el disc en el gràfic interactiu perquè el raig incideixi amb els angles indicats, mira què val l'angle θ2 i anota'l a la taula.
Calcula sin(θ2)/sin(θ1). Quina conclusió extreus?
Una conclusió rellevant mostrar
La tercera columna de la taula amb sin(θ2)/sin(θ1) dona un valor molt proper a 1.52 en totes les files. L'observació suggereix que, aquest quocient és constant. Això és una part de la llei de Snell que també assigna índexs de refracció als medis transparents.
ocultar Pots repetir la taula:
1) Girant el disc graduat perquè el raig entri per la cara plana.
2) Canviant el prisma amb el botó [Canvia prisma].

En el gràfic interactiu es mostra un raig reflectit a més del raig refractat. La intensitat de la llum del raig incident es reparteix entre el raig reflectit i el raig refractat.
Amb el raig incident per la cara circular, observa:
Per a θ2 petit, el color del raig reflectit a la cara plana es un vermell fluix. Representa que la intensitat del raig reflectit és petita.
Quan θ2 augmenta, el color del raig reflectit va augmentant i el color del raig refractat disminueix.
Amb el prisma inicial, per damunt de θ1 = 40°, el raig refractat té molt poca intensitat i acaba desapareixent. Això es pot entendre perquè
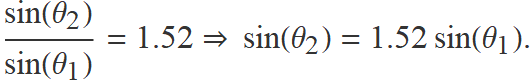
Aquesta igualtat és imposible de verificar si sin(θ1) és més gran que 1/1.52 perquè el terme dret serà més gran que 1 i el sin(θ2) és menor o igual que 1.
L'angle d'incidència θ1 ha de ser igual o menor que l'angle θ1,límit tal que
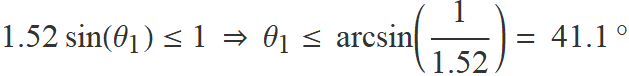
El valor més alt que pot tenir θ1 es denomina angle límit,
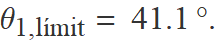
La intensitat del raig refractat disminueix quan θ1 augmenta i s'anul·la quan arriba a l'angle límit. per a un angle igual o superior a l'angle límit, tota la llum incident es reflecteix. Es diu que es produeix reflexió total de la llum.
Observa que si el raig arriba al prisma per la cara plana, no hi ha angle límit. L'angle límit només es dona quan l'angle del raig refractat és més gran que l'angle del raig incident. Això no passa quan el raig es refracta a la cara plana i entra dins el prisma.
