
Camp gravitatori

Uns 80 anys després de la formulació de les lleis del moviment planetari de Kepler, Isaac Newton va donar l'explicació de perquè els planetes orbitaven el Sol d'acord amb aquelles lleis.
En el llibre "Philosophiæ Naturalis Principia Mathematica", publicat el 1687, Newton va formular la famosa llei de la gravitació universal:
«Cada partícula de matèria de l'univers atreu cada altra partícula amb una força que és directament proporcional al producte de les masses i inversament proporcional al quadrat de la distància que les separa.»
El Sol i els planetes eren com a esferes i quan se sumava l'atracció entre totes les seves partícules el resultat era que:
Dues esferes de masses M1 i M2 s'atreuen amb força que és directament proporcional al producte de les masses i inversament proporcional al quadrat de la distància entre els centres de les esferes.
Newton aplicà la llei de gravitació universal per calcular la trajectòria d'un planeta al voltant del Sol y va trobar les lleis de Kepler matemàticament.
1)
De la resolució de l'equació del moviment d'un planeta subjecte a l'atracció gravitatòria del Sol trobà que la trajectòria tancada és una òrbita el·líptica amb el Sol en el focus de l'el·lipse. Això era la primera llei.
2)
També va trobar que s'havia de complir la segona llei o llei de les àrees perquè el camp gravitatori era central (la força sobre un planeta sempre estava dirigida cap al centre del Sol).
3)
I, analitzant la relació entre la mida de l'òrbita determinada pel semieix major a i el període orbital T, va trobar que
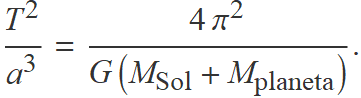
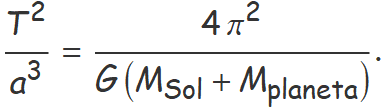
Atès que la massa del Sol era molt més gran que la de qualsevol planeta, el quocient seria essencialment igual per a tots els planetes del sistema solar, com establia la tercera llei de Kepler.
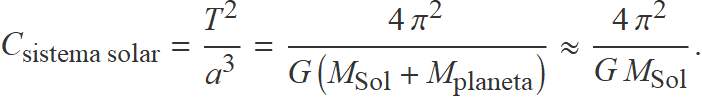
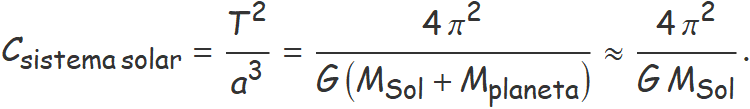
Usant el valor de la massa del Sol i passant el temps a anys i la distància a unitats astronòmiques, s'obté
Csistema solar = 1.0000 a2 au−3.
L'explicació de les lleis de Kepler amb la teoria de la gravitació de Newton va transformar l'astronomia i impulsar la branca de la Física clàssica que es diu Mecànica.

L'explicació de les lleis de Kepler recolzava la validesa de la teoria de Newton, que tingué un èxit quan serví per descobrir Neptú.
Es coneixien cinc planetes des l'antiguitat: Mercuri, Venus, Mart, Júpiter i Saturn. El 13 de març de 1781, William Herschel va veure amb un telescopi el que es confirmaria era, comptant la Terra, el seté planeta conegut del sistema solar, i es denominà Urà.

El seguiment precís amb telescopis dels moviments de Júpiter, Saturn i Urà mostrà que no es comportaven exactament tal com predia la teoria de Newton. Els francesos Urbain Le Verrier i Heinrich d’Arrest, calcularen la posició d'un planeta hipotétic perquè el moviment dels planetes fos com l'observada d'acord amb les lleis de Newton. L'astrònom anglès Johm Adams, independentment, també va fer un càlcul aproximat de la posició d'un planeta hipotètic. El 23 de setembre de 1846, l'astrònom alemany Johann Galle va trobar un planeta a menys d'un grau de la posició indicada per Le Verrier. Aquest planeta s'anomenà finalment Neptú i és el vuité planeta del sistema solar.


Les lleis de Kepler es poden aplicar als cometes quan es mouen lluny dels planetes.
Quan un cometa passa a prop d'un planeta està sotmès a dues forces d'atracció gravitatòria, la del Sol i la del planeta, i no només a l'atracció del Sol. Quan la influència del planeta torni ser irrellevant i la força dominant sobre el cometa sigui només l'atracció del Sol, l'òrbita seguirà una altra el·lipse amb el Sol en un focus. El semieix major d'aquesta el·lipse serà un poc diferents al de l'el·lipse que seguia el cometa abans de passa a prop del planeta. Com que la mida de l'el·lipse i el període orbital estan relacionats, el període orbital també haurà canviat un poc.
El valor de T2/a3 pels cometes movent-se lluny dels planetes és el mateix que s'obté pels planetes,
Csistema solar = 1 a2 au−3.

Isaac Newton va deduir les lleis de Kepler calculant el moviment d'una massa atreta per una massa molt més gran. Les lleis de Kepler s'apliquen a tots els cossos que es mouen dins el camp gravitatori d'un únic objecte de massa molt més gran.
Les lleis de Kepler també es poden aplicar, sabent que és una aproximació, a les òrbites de les llunes d'un planeta gran com Júpiter perquè l'atracció del planeta és més gran que la del Sol.
El valor constant de T2/a3 dependrà del planeta que orbiten i, evidentment, serà diferent a Csistema solar. La lluna més gran de Júpiter (i de tot el sistema solar) és Ganimedes. Té un període orbital al voltant de Júpiter de 171 h i el semieix major de l'òrbita té 1070400 km. Amb aquests valors, T2/a3 val
Cllunes Júpiter ≈ 1040 a2 au−3.

No, la llei de Newton no és exacta. La llei de la força gravitatòria de Newton és una aproximació bona, però s'ha comprovat que perd validesa quan la intensitat del camp gravitatori es gran. De fet, la teoria general de la relativitat no tracta la gravetat com una força.
