
Bloc


El moviment oscil·latori d'un punt és un desplaçament repetit al voltant d'una posició d'equilibri. Algunes oscil·lacions es diuen vibracions.
Per la descripció matemàtica, alguns moviments oscil·latoris es diu que són harmònics i, entre aquests, hi ha els harmònics simples.
El moviment oscil·latori s'anomena vibració quan les oscil·lacions són ràpides i d'amplitud relativament petita. Els punts que se sol dir que vibren són de:
• La corda d'una guiterra.
• El telèfon mòbil quan rep una notificació.
• Un vehicle vell amb el motor engegat.
Un moviment oscil·latori d'un punt és harmònic quan la seva posició es pot calcular com a suma de funcions sinusoidals.
• La membrana d'un alteveu oscil·la amb un moviment harmònic quan reprodueix música.
Un moviment oscil·latori d'un punt és harmònic simple si el desplaçament y(t) respecte de la posició d'equilibri és pot expressar amb la funció sinus:
y(t) = A sin(ω t + δ)
Tenen moviments harmònics simples:
• Una massa que oscil·la verticalment penjada d'una molla de massa negligible.
• El braços d'un diapasó després de colpejar-ho.
• La massa d'un pèndol simple quan les oscil·lacions són molt petites.
Un moviment oscil·latori pot ser que sigui no harmònic.
• La massa d'un pèndol simple que oscil·la amb una amplitud gran és no harmònic perquè el moviment és repeteix però la posició de la massa no es pot determinar amb una suma de funcions sinusoidals.

La funció sinusoidal
y(t) = A sin(ω t + δ)
s'usa en l'estudi del moviment oscil·latori harmònic simple amb:
• A: amplitud de l'oscil·lació,
• ω (omega): freqüència angular (rad/s),
• δ (delta): fase inicial o desfase (rad)
El recorregut de la funció y(t) és [−A, A]. Aquí es considerarà que A té unitats de longitud.
La fase inicial δ, també anomenada desfase, determina les posicions dels extrems i els zeros de y(t). Si la fase inicial s'expressa en graus s'ha de convertir a radians per sumar a ω t.
La periodicitat de y(t) és
T = 2π/ω.
L'interval entre dos màxims de y(t) (o entre dos mínims) és T.
L'interval entre dos zeros de y(t) és T/2.
El cosinus també s'usa per descriure el moviment oscil·latori harmònic simple perquè les funcions sinus i cosinus estan relacionades. Per exemple,
sin(α) = cos(α − π/2),
cos(α) = sin(α + π/2).
Així,
y(t) = A cos(ω t + ε) = A sin(ω t + δ),
amb la fase inicial
ε = δ − π/2
Els valors de l'argument α dins l'interval [0, 2π) per els quals les funcions sin(α) i cos(α) tenen els valors minim (−1), nul (0) i màxim (1) són sempre multiples de π/2.
Atès que sin(α + n 2π) = sin(α) i cos(α + n 2π) = cos(α) per a n sencer, es té
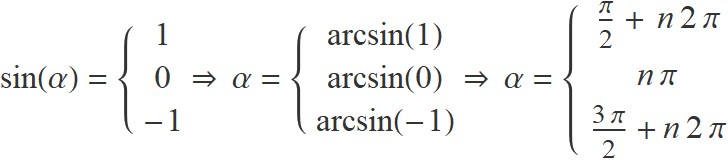

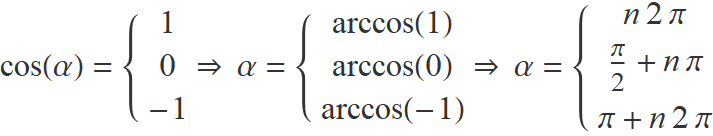
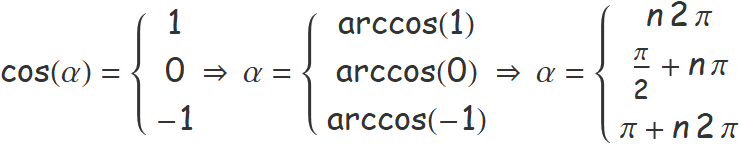
n = 0, ±1, ±2,...

Si dubtes quan necessitis algun d'aquests resultats, usa la calculadora per trobar el valor de l'angle dins l'interval [0, 2π) amb la funció arcsinus o arccosinus i suma n π a l'angle si el valor de la funció és nul i n 2π en altre cas.
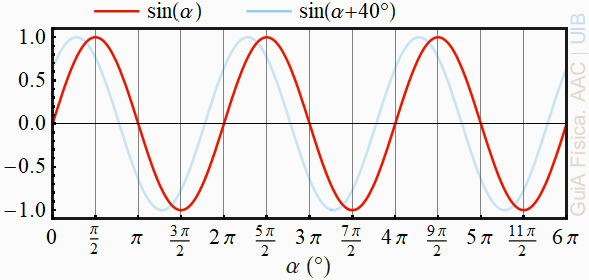
La funció sin(α) és nul·la a α = 0. El gràfic següent mostra la funció sin(α) (linia violeta) i la funció sin(α + 40°) (cel). Com que la fase inicial és positiva, aquesta segona funció arriba al màxim més aviat i sembla que la corba s'ha desplaçat cap a l'esquerra.
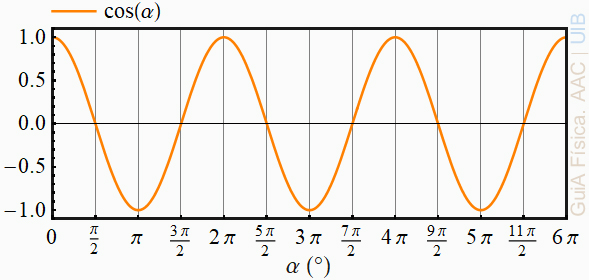
La funció cos(α) és màxima a α = 0. El gràfic següent mostra la funció cos(α) (linia taronja). Posa el cursor sobre la imatge per sobreimposar la funció sinus.

La velocitat d'un punt que té la posició donada per la funció
y(t) = A sin(ω t + δ)
es determina amb la derivada de y(t) respecte del temps,
v(t) = A ω cos(ω t + δ)
L'acceleració associada al moviment anterior es determina amb la derivada de la velocitat respecte del temps
a(t) = −A ω2 sin(ω t + δ)
L'acceleració d'un punt que té un moviment harmònic simple es pot calcular directament a partir de la posició,
a(t) = −ω2 y(t)

Es considera un sistema format per una esfera de massa m lligada a una molla de massa negligible, longitud natural L0 i constant elàstica k.
Los unitats de la constant elàstica k són
[k] = N/m = kg/s2.
Només es tractaran oscil·lacions horitzontals o en absència de gravetat. L'energia mecànica del sistema és la suma de l'energia elàstica de la molla més l'energia cinètica de l'esfera.
L'energia potencial elàstica d'una molla estirada fins a una longitud L des de la seva longitud natural L0 es calcula a partir del treball per estirar la molla.
La força per estirar una molla és igual a la constant elàstica k per l'elongació x de la molla (l'elongació és la longitud de la molla menys la longitud natural). Així, el treball per estirar la molla des de l'elongació 0 fins a l'elongació L − L0 és
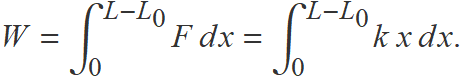
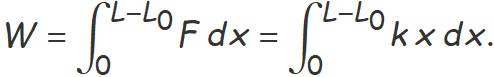
La integració és immediata i s'obté
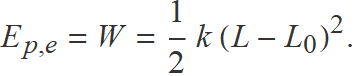
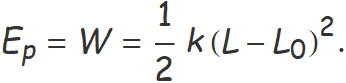
En el moviment harmònic simple, l'elongació L − L0 durant les oscil·lacions és calcula amb la funció
y(t) = A sin(ω t + δ).
Per tant,
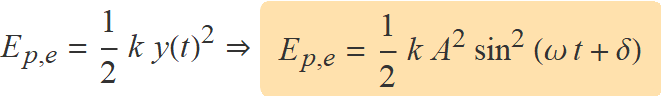
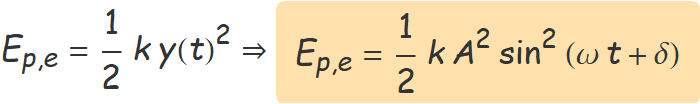
L'energia cinètica de l'esfera és
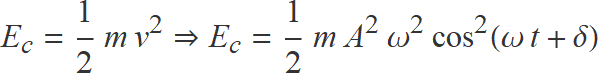
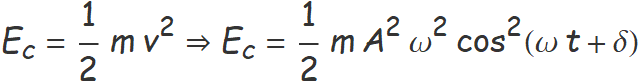
Atès que ω = (k/m)1/2, l'energia cinètica es pot escriure en la forma
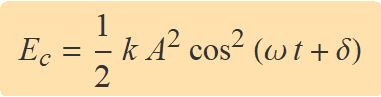
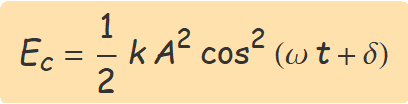
L'energia mecànica del sistema, donat que cos2(α) + sin2(α) = 1, és
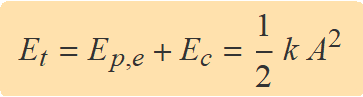
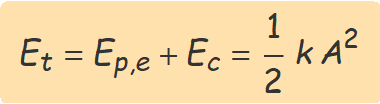

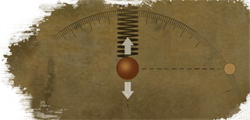
Una esfera penjada d'una molla està aturada en la posició d'equilibri a una altura yeq, on el pes i la força elàstica de recuperació de la molla s'igualen. Quan l'esfera s'estira una distància A cap avall, la posició de l'esfera des del moment que s'amolli serà
y(t) = yeq + A sin(ω t − π/2)
o
y(t) = yeq + A cos(ω t − π).
S'ha de notar que y(0) = yeq − A.
La coordenada vertical d'un punt que dona voltes a velocitat constant sobre una circumferència de radi A centrada en el punt d'equilibri de la bolla penjada de la molla, està donada per la mateixa funció y(t) amb la que s'obté la posició de l'esfera. La figura il·lustra aquest fet. La línia discontinua entre el punt sobre la circumferència i l'esfera que oscil·la s'ha dibuixat com a referència. (Pitja sobre la imatge per reiniciar la reproducció.)


Calcula el període de la funció
y(t) = A sin(0.4 t + π/5)
i determina els tres primers temps positius quan la funció y(t) és nul·la i el tres primers quan és màxima.
Resolució mostrar

La freqüència angular és ω = 0.4 rad/s. Per tant,
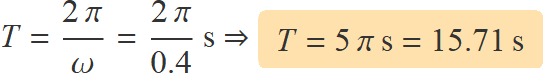
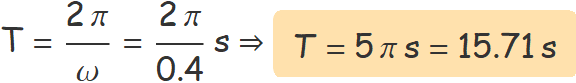

S'han determinar els temps quan el sinus val zero:
sin(0.4 t + π/5) = 0 ⇒ 0.4 t + π/5 = n π, n = 0, ±1, ±2,...
Aïllant el temps, la funció és nul·la per a
t = (π/2) (5 n − 1), n = 0, ±1, ±2,...
Els tres primers temps positius quan la funció val zero, s'obtenen amb n = 1, 2 i 3:
y(t) = 0 per a t = 2π s, 9π/2 s, 7π s
Es pot comporvar que el temps entre dos zeros és la meitat del període.

S'han determinar els temps quan el sinus val 1:
sin(0.4 t + π/5) = 1 ⇒ 0.4 t + π/5 = (π/2) + n 2π, n = 0, ±1, ±2,...
Aïllant el temps, el sinus val 1 per a
t = (π/2) (5 n − 1), n = 0, ±1, ±2,...
Els tres primers temps positius quan la funció val 1, s'obtenen amb n = 1, 2 i 3:
y(t) = A per a t = 3π/4 s, 23π/4 s, 43π/4 s
Es pot comporvar que el temps entre dos màxims és el període.
ocultar

Calcula els tres primers instants quan la següent funció es mínima.
y(t) = A sin(1.2 t + 30°).
Resolució mostrar
S'han determinar els temps quan el sinus val −1:
La fase inicial s'ha d'expressar en radians,
30° = π/6 rad.
Així,
sin(1.2 t + π/6) = −1 ⇒ 1.2 t + π/6 = (3π/2) + n 2π, n = 0, ±1, ±2,...
Aïllant el temps, la funció és nul·la per a
t = (5π/9) (3n + 2), n = 0, ±1, ±2,...
Els tres primers temps positius quan la funció és mínima, s'obtenen amb n = 0, 1 i 2:
y(t) = −A per a t = 10π/9 s, 25π/9 s, 40π/9 s
El temps entre dos mínims és el període 5π/3 s = 15π/9 s.
ocultar

Donada la funció
y(t) = A cos(2t − 30°),
calcula els tres primers instants quan la funció és nul·la, màxima i mínima.
Resolució mostrar

S'han determinar els temps quan el cosinus val 0:
La fase inicial s'ha d'expressar en radians,
−30° = −π/6 rad
cos(2t − π/6) = 0 ⇒ 2t − π/6) = π/2 + n π, n = 0, ±1, ±2,...
Aïllant el temps, la funció és nul·la per a
t = π/3 + n π/2, n = 0, ±1, ±2,...
Els tres primers temps positius quan la funció és nul·la, s'obtenen amb n = 0, 1 i 2:
y(t) = −A per a t = π/3 s, 5π/6 s, 4π/3 s
Es pot comprovar que els temps entre dos zeros és la meitat del període (π/2 s).

S'han determinar els temps quan el cosinus val 1:
La fase inicial s'ha d'expressar en radians,
−30° = −π/6 rad
cos(2t − π/6) = 1 ⇒ 2t − π/6) = n 2π, n = 0, ±1, ±2,...
Aïllant el temps, la funció és nul·la per a
t = π/12 + n π, n = 0, ±1, ±2,...
Els tres primers temps positius quan la funció és mínima, s'obtenen amb n = 0, 1 i 2:
y(t) = −A per a t = π/12 s, 13π/12 s, 25π/12 s
Es pot comprovar que els temps entre dos mínims és el període π s.

S'han determinar els temps quan el cosinus val −1:
La fase inicial s'ha d'expressar en radians,
−30° = −π/6 rad
cos(2t − π/6) = −1 ⇒ 2t − π/6) = π + n 2π, n = 0, ±1, ±2,...
Aïllant el temps, la funció és nul·la per a
t = 7π/12 + n π, n = 0, ±1, ±2,...
Els tres primers temps positius quan la funció és mínima, s'obtenen amb n = 0, 1 i 2:
y(t) = −A per a t = 7π/12 s, 19π/12 s, 31π/12 s
Es pot comprovar que els temps entre dos mínims és el període π s.
ocultar

La freqüència angular ω de les oscil·lacions verticals d'una massa m penjada d'una molla de constant elàstica k és
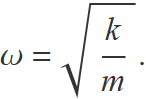
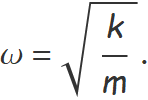
Les unitats de la constant elàstica són kg/s2.
a) Una esfera de massa m i una de massa 2m estan penjades de molles iguals. Quina oscil·la més ràpidament?
b) Una esfera oscil·la més ràpidament penjada d'una molla de constant elàstica gran o petita?
c) Una esfera de massa m es penja d'una molla de constant elàstica 56 kg/s2 i una altra esfera de la mateixa massa, es penja d'una altra molla. Es determina que aquesta segona esfera oscil·la amb un període que és el doble del període d'oscil·lació de la primera esfera. Què val la constant elàstica de la segona molla?
Resolució mostrar

Una freqüència més gran indica oscil·lacions més ràpides.
D'acord amb l'expressió de la freqüència angular donada a l'enunciat, ω és més gran com més petita és la massa que penja de la molla.
Per tant, l'esfera de massa m oscil·la més ràpid que l'esfera de massa 2m.
L'esfera de massa petita oscil·la més ràpid

Una freqüència més gran indica oscil·lacions més ràpides.
D'acord amb l'expressió de la freqüència angular donada a l'enunciat, ω és més gran com més gran és la constant elàstica de la molla.
Per tant, l'esfera oscil·la més ràpid quan està penjada de la molla de constant elàstica més gran.
L'esfera oscil·la més ràpid penjada d'una
molla de constant elàstica gran

L'enunciat indica que
T2 = 2 T1.
El període de les oscil·lacions es pot escriure en funció de la massa i la constant elàstica usant l'expressió de la freqüència angular donada a l'enunciat:
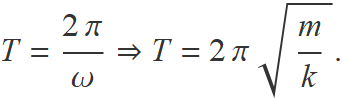
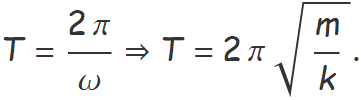
Per tant,
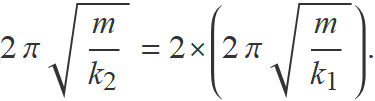
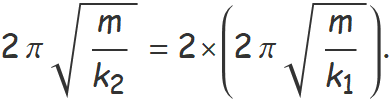
Simplificant termes y elevant els dos membres al quadrat es troba
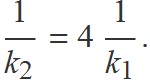
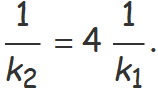
Usant k1 = 56 kg/s2 i aïllant k2 sobté
k2 = 14 kg/s2
ocultar
Una esfera de 16~kg està penjada d'una molla de constant elàstica 512 kg/s2. Des de la posició d'equilibri de l'esfera, s'estira 2 cm cap avall i s'amolla. L'esfera comença a oscil·lar verticalment amb un moviment harmònic simple. El desplaçament vertical y(t) respecte de la posició d'equilibri es pot descriure amb la funció sinus o amb la funció cosinus
a) Escriu y(t) usant la funció sinus.
b) Escriu y(t) usant la funció cosinus.
c) Determina el període de les oscil·lacions.
d) Des de que s'ha amollat l'esfera perquè oscil·li quan de temps passa fins que l'esfera arriba cinc vegades al punt més alt de l'oscil·lació.
Resolució mostrar

L'amplitud de l'oscil·lació és la distància que s'estira cap a baix,
A = 0.02 m.
La freqüència angular és
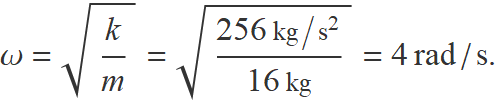

La funció que descriu el deplaçament des de la posició d'equilibri és
y(t) = 0.02 m sin(4 t + δ).
La fase inicial δ es determina amb el valor de la funció a t = 0:
y(0) = 0.02 m sin(δ) = −0.02 m ⇒ sin(δ) = −1.
Per tant, δ = arcsin(−1). Les solucions són
δ = 3π/2 + n 2π, n = 0, ±1, ±2,...
Es podria usar qualsevol d'aquestes solucións. Si es calcula arcsin(−1) amb una calculadora, es pot obtenir la solució corresponent a n = −1 que és δ = −π/2. Usant aquest valor, es tendrà
y(t) = 0.02 m sin(4 t − π/2)

L'amplitud i la freqüència angular no canvien, només canvia la fase inicial ε. per tant,
y(t) = 0.02 m cos(4 t + ε).
La fase inicial δ es pot determinar per per la relació entre el cosinus i el sinus
ε = δ − π/2 = −π/2 − π/2 ⇒ −π
Amb el valor de la funció a t = 0, es tendrà
y(0) = 0.02 m cos(ε) = −0.02 m ⇒ cos(ε) = −1.
Per tant, ε = arccos(−1). Les solucions són
ε = ±π, ±3π, ±5π, ...
Es pot usar qualsevol d'aquestes solucions com a fase inicial. Usarem la que s'ha donat per la relació entre el cosinus i el sinus:
y(t) = 0.02 m cos(4 t − π)

El període es calcula a partir de la freqüència angular ω = 4 rad/s, obtinguda en el primer apartat:
T = 2π/ω ⇒ T = π/2 s


Hi ha moviments que són oscil·lacions però no són harmònics i moviments que són oscil·lacions harmòniques però no són harmònics simples. El moviment oscil·latori harmònic simple és el que té la descripció matemàtica més senzilla.

1
Un moviment harmònic simple d'una massa es descriu amb la següent funció del temps en segons:
y(t) = 4 cm cos(2.7 t + 25°).
a) Què val y a t = 1 s?
b) Què val la velocitat vertical en cm/s de la massa oscil·lant a t = 2 s?
c) Quina és la velocitat màxima de la massa en cm/s?
2
La freqüència angular de les oscil·lacions verticals harmòniques d'una massa de m = 0.15 kg penjada d'una molla de constant elàstica k és
ω = (k/m)1/2.
El desplaçament amb relació a la posició d'equilibri és, amb el temps donat en segons,
y(t) = 3 cm sin(2.7 t − 1.2 rad).
Calcula:
b) La constant elàstica de la molla.
a) La velocitat en cm/s quan el desplaçament és de 2.2 cm.
3
Les oscil·lacions verticals d'una esfera de 280 grams penjada d'una molla de constant elàstica k = 37 kg/s2 tenen un període
T = 2π (m/k)1/2.
L'esfera oscil·la amb una amplitud de 2 cm. A t = 0, l'esfera passa per la posició d'equilibri cap a baix. A quin primer temps després d'aquest instant, l'esfera està en el punt més alt de l'oscil·lació?
4
Es mesura la posició del centre de masses d'una esfera penjada d'una molla amb relació a un punt de referència fix. El punt de referència és troba per baix de la posició d'equilibri. Amb les dades, es fa el gràfic de la posició y(t) mostrat a la figura.
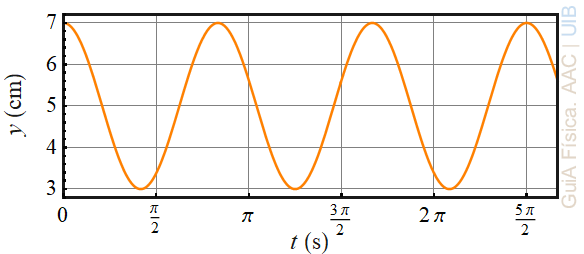
a) Quina és l'amplitud en cm de les oscil·lacions?
b) Què val el període de les oscil·lacions?
c) S'ha d'usar els sinus o el cosinus per escriure la funció y(t) amb una fase inicial zero?
5
Entres en un laboratori i veus dues esferes de la mateixa mida oscil·lant com mostra la imatge adjunta. (Pitja sobre la imatge per reiniciar la reproducció.)
Et comenten que les dues molles tenen la mateixa constant elàstica.
a) A partir de les oscil·lacions observades, l'esfera que té més massa és la de l'esquerra o la de la dreta? Justifica la resposta.
b) Quantes oscil·lacions completes fa l'esfera esquerra en el temps que dura la reproducció de la imatge?
c) I l'esfera dreta?
d) Si la massa de l'esfera dreta és de 0.4 kg, quina és la massa de l'esfera esquerra?
