Exercici 0

Recorda que la simetria d'un sistema de càrregues elèctriques queda reflectit en la simetria del seu camp.
Una distribució de càrrega que només depèn de la distància a l'origen de coordenades, té simetria esfèrica i el seu camp també: El camp tendrà direcció radial i un mòdul funció només de la distància a l'origen.

Atès que la càrrega elèctrica de la closca de l'enunciat està distribuïda uniformement sobre una superfície esfèrica, el camp elèctric, si no és nul, és radial i la intensitat només depèn de la distància r al centre de les closques.

Amb la llei de Gauss, s'ha calculat en aquest exercici que el camp en un punt d'un superficie esfèrica de radi r val

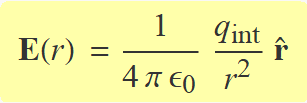
on q_int és la càrrega total dins la superfície.

Les superfícies esfèriques de 4 cm i 11.9 cm són més petites que el radi de la closca, per tant, no hi ha càrrega elèctrica en el seu interior. de manera que

E(4 cm) = 0
E(9 cm) = 0

Les superfícies esfèriques de 12.1 cm i 20 cm contenen la càrrega total de la closca esfèrica:

q_int = Q = (4π R²) σ₀ = 0.9048 nC.

Amb l'Eq. (1) s'obté

E(12.1 cm) = 0.556 μN/C
E(20 cm) = 0.204 μN/C