Exercici 0
Camp magnètic de fils. Llei de Biot Savart

Solució mostrar
La llei de Biot-Savart estableix la contribució d'un segment de longitud diferencial ds al camp magnètic a un punt situat a la posició relativa r del segment,
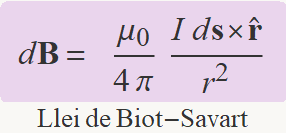
S'ha de recordar que quan el fil no és recte, ds és un vector de direcció tangent al fil i de sentit cap a on va el corrent. També s'ha de recordar que el vector r va del punt del fil fins al punt on es calcula el camp i no al revés.
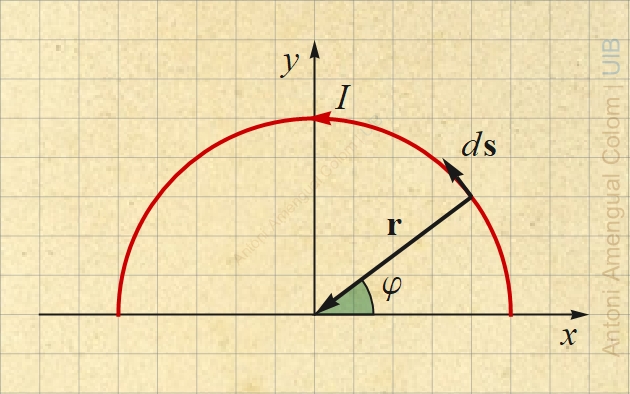
S'usaran un eixos de coordenades cartesianes amb origen al centre de curvatura de l'arc com mostra la Fig. 1. Les coordenades de tots els punts de l'arc semicircular de radi R són
x(t) = R cos(φ),
y(t) = R sin(φ),
φ ∈ [0, π].
El vector r que va d'un punt de l'arc a l'origen de coordenades és
r = R (−cos(φ), −sin(φ), 0).
El mòdul de r és el radi R, igual per a tots els punts de l'arc.
Com que r s'ha determinat en funció de l'angle φ, el vector ds també s'escriurà en funció d'aquest angle. El vector ds és tangent a l'arc i, com que la tangent en un punt d'un arc circular és perpendicular al radi, el vector és perpendicular a r. El vector unitari 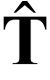 perpendicular a r i que marca en el sentit antihorari (com el corrent elèctric) és
perpendicular a r i que marca en el sentit antihorari (com el corrent elèctric) és
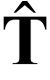 = (−sin(φ), cos(φ), 0).
= (−sin(φ), cos(φ), 0).
La longitud del vector ds és la d'un arc d'angle dφ i val R dφ. Així es tendrà
ds = R dφ 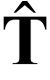 = R (−sin(φ), cos(φ), 0) dφ.
= R (−sin(φ), cos(φ), 0) dφ.
Abans de substituir termes dins l'Eq. (1), es farà el producte vectorial del numerador
ds × r = (0, 0, 1) R dφ = R dφ 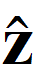 .
.
La llei de Biot-Savart proporciona el camp a causa del corrent que passa per un element ds de l'arc,
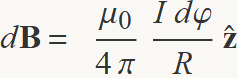
El camp total és la suma de tots els elements de l'arc,
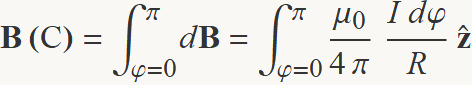
La integració és immediata,
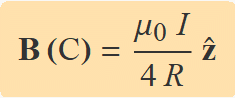
Com cal esperar, aquest resultat és la meitat del camp a causa d'un corrent en un anell de radi R. Per a un anell, els límits de la integral Eq. (2) serien 0 i 2π. La mateixa integral mostra que la contribució al camp magnètic d'un fil amb forma d'arc circular d'angle θ és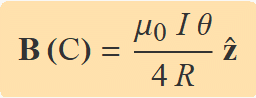
b) La contribució dels trams rectes del circuit al camp en el centre de curvatura dels arcs és zero perquè el vector r des de qualsevol punt dels trams rectes fins el centre és paral·lel al vector ds, i el producte vetorial de dos vectors paral·lels que apareix en el numerador de la llei de Biot-Savart, és zero.
El camp magnètic en el centre dels arcs és la suma dels camps de cada arc. Es pot usar l'Eq. (3) per a l'arc petit de radi R1 directament i per a l'arc gran de radi R2, pensant que el corrent va en sentit horari i el camp té el sentit de −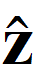 ,
,
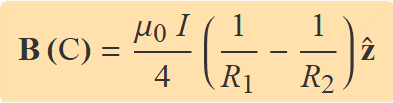


Text, gràfics i disseny d'aquest lloc web:
Antoni Amengual Colom (Revisat: 2023), Departament de Física

Els continguts d'aquestes pàgines es poden usar sense modificar, retallar o refer amb finalitat educativa, sense ànim de lucre, citant l'autor de les pàgines i posant en lloc visible l'adreça d'aquest lloc web. Usau: "Exercicis d'Electromagnetisme· Antoni Amengual Colom · UIB url: http://dfs.uib.es/apl/aac/FGII23/".
 Índex lista
Índex lista Exercici anterior
Exercici anterior Exercici posterior
Exercici posterior