Índex lista
Exercici anterior
Exercici posteriorExercici 0
Llei de Gauss
Respostes mostrar
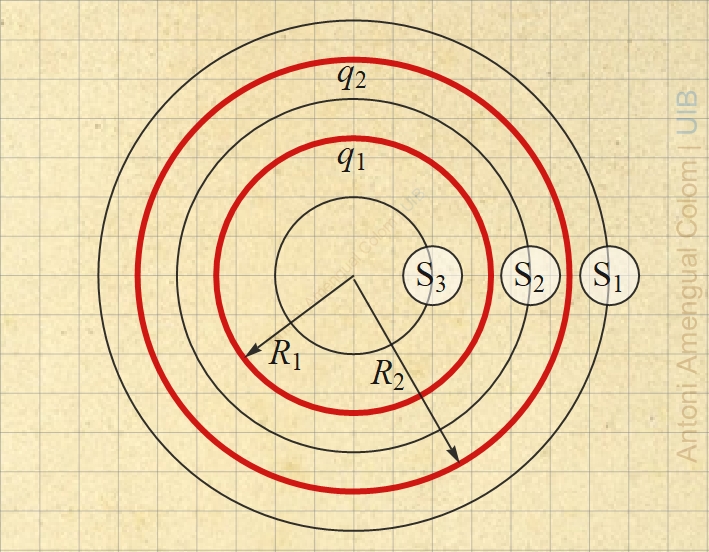
El càlcul del camp s'ha de fer per a l'espai exterior, entre les dues superfícies i dins la superfície de radi petit.
Per la simetria de les distribució de les càrregues, el camp elèctric és radial i la intensitat només depèn de la distància r al centre de les esferes,
E(r) = E(r)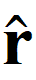 
.
El flux del camp a través d'una superfície esfèrica Sr de radi r concèntrica amb les superfícies de l'enunciat es pot demostrar que val
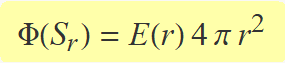
Intentau fer la demostració abans d'obrir el requadre que apareix després de l'Eq. (4).
Si la càrrega neta tancada per Sr és qint, la llei de Gauss estableix que el flux ha de valer
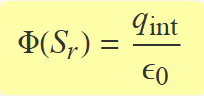
Igualant les Eqs. (2) i (3), es pot aïllar la intensitat del camp a una distància r. Llavors, l'Eq. (1) permet escriure el camp elèctric vectorial
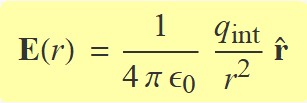
Demostració Eq. (2) mostrar
El flux del camp a través d'una superfície esfèrica Sr de radi r, concèntrica amb les superfícies on hi ha les càrregues és
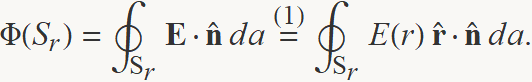
Els vectors normals a la superfície en tots els punts de S són sempre radials,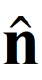 
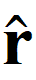= , de manera que
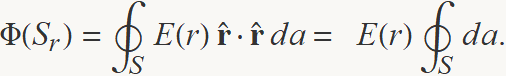
La integral dels diferencials d'àrea sobre la superfície esfèrica de radi r és igual a l'àrea de tota l'esfera, llavors
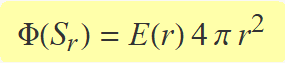
Aquesta és l'expressió que s'havia de demostrar.
ocultarZona exterior (r > R2)
Per calcular el camp en aquesta zona, es considera una superfície esfèrica S1 de radi r > R2.
La càrrega neta total dins S1 és
qint = q1 + q2.
Aquesta càrrega se substitueix dins l'Eq. (4) i s'obté la intensitat del camp en aquesta zona. El camp en forma vectorial és
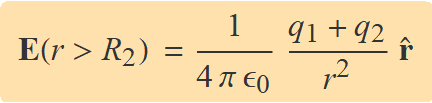
Zona intermèdia (R1 < r < R2)
Per calcular el camp en aquesta zona, es considera una superfície esfèrica S2 de radi r, tal que R1 < r < R2.
La càrrega neta total dins S2 és
qint = q1.
Aquesta càrrega se substitueix dins l'Eq. (4) i s'obté la intensitat del camp en aquesta zona. El camp en forma vectorial és
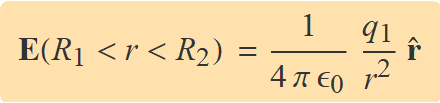
Zona interior (r < R1)
Per calcular el camp en aquesta zona, es considera una superfície esfèrica S3 de radi r, tal que r < R1.
La càrrega neta total dins S3 és zero, per tant,
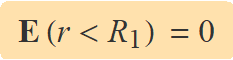
Text, gràfics i disseny d'aquest lloc web:
Antoni Amengual Colom (Revisat: 2023), Departament de Física
Els continguts d'aquestes pàgines es poden usar sense modificar, retallar o refer amb finalitat educativa, sense ànim de lucre, citant l'autor de les pàgines i posant en lloc visible l'adreça d'aquest lloc web. Usau: "Exercicis d'Electromagnetisme· Antoni Amengual Colom · UIB url: http://dfs.uib.es/apl/aac/FGII23/".