Exercici 0

Amb els eixos de coordenades amb origen en el centre del disc i el disc contingut en el pla x-y, l'eix z serà l'eix sobre el que s'ha de calcular el camp.

El camp elèctric té la direcció de l'eix z perquè el disc té simetria de rotació al voltant d'aquest eix.

Una manera de calcular el camp a causa de la càrrega distribuïda sobre el disc és a partir del camp a causa d'un anell de càrrega q i radi a,

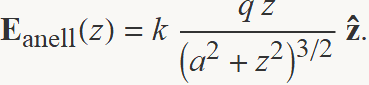
Una part del disc entre els radis r i r + dr crea un camp com el d'un anell de radi r amb una càrrega igual a l'àrea de l'anell de gruix infinetesimal per la densitat de càrrega.

dq = da σ₀ = (2πr dr) σ₀.

Cal fixar-se que l'àrea da de l'anell de gruix infinitesimal és igual a la longitud de la circumferència de radi r pel gruix dr. Quan s'integra da des de r = 0 fins r = a, el resultat és π a² que és l'àrea del disc.

El camp a causa del disc és igual que la suma (integració) dels camps de tots els anells des de r = 0 fins r = a:

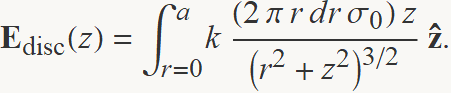
Es necessita fer una integral que és immediats

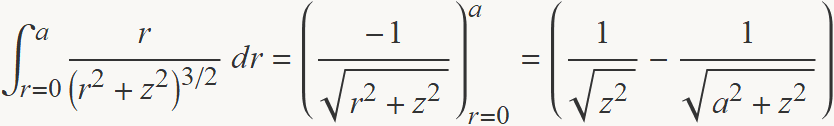
Substituint el resultat de la integral dins l'Eq. (1) i usant k = 1/(4πε₀), s'obté

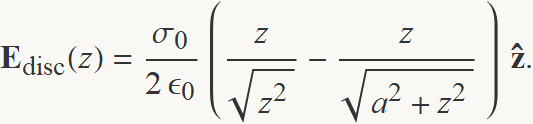
Si z = z_p > 0, el primer terme entre parèntesis val 1 i es pot escriure

En els punts de l'eix z positiu, el camp apunta en la direcció cap a dalt si σ₀ > 0. En ls punts de l'eix z negatiu, el camp apunta cap a baix. L'expressió que serveix per a qualsevol punt de l'eix z és

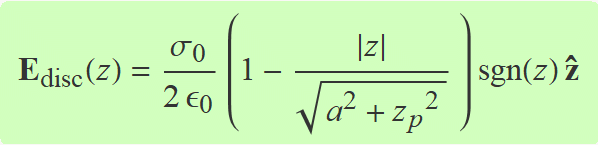
S'usa la funció sgn(z) que és igual a 1 si z és positiu i −1 si z és negatiu.