Índex lista
Exercici anterior
Exercici posteriorExercici 0
Potencial elèctric, energia i treball
Solució mostrar
a) El camp elèctric a tot l'espai és radial i el mòdul només depèn de la distància r al centre perquè la densitat de càrrega només depèn de r.
El camp en un punt a una distància r es pot calcular amb la llei de Gauss aplicada a una superfície esfèrica S de radi r,
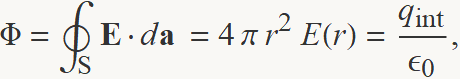
on qint és la càrrega tancada per S. Aïllant el camp, s'obté
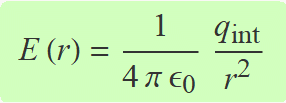
Per a un punt fora del nigul, la càrrega tancada per S és la càrrega total Q del nigul.
L'Eq. (1) proporciona el camp fora del nigul,
Aquest camp és el mateix que es tendria amb tota la càrrega concentrada en el centre del nigul.
Per a un punt dins el nigul, la càrrega tancada per la superfície S de radi r és
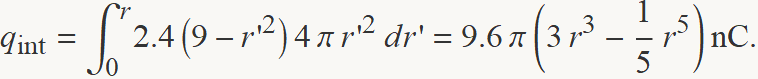
L'Eq. (1) proporciona el camp dins el nigul,
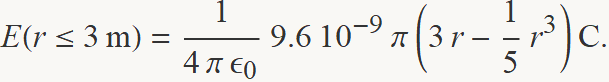
El terme 1/(4π ε0) és la constant de Coulomb. Si se substitueix pel valor numèric s'obté
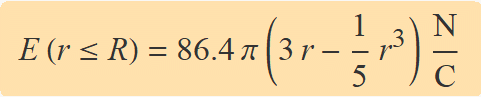
b) S'ha de determinar la diferència de potencial entre un punt A a 1.5 m del centre del nigul i un punt B a 2 m del centre. Els dos punts estan dins el nigul de 3 m de radi. La diferència de potencial es calcula amb l'expressió:
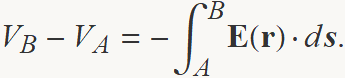
Per la simetria esfèrica, les superfícies equipotencials són esfèriques, de manera que la diferència de potencial entre A i B només depèn de les distàncies al centre i es pot calcular suposant que els dos punts estan sobre la mateixa direcció radial per a la qual es té
ds = dr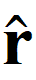 
.
Atès que el camp elèctric és radial,
E(r) · ds = E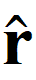(r) · dr 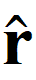= E(r) dr.
Amb l'expressió del camp Eq. (2) s'ha d'avaluar la integral següent
El resultat de la integració és
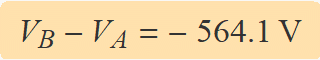
Text, gràfics i disseny d'aquest lloc web:
Antoni Amengual Colom (Revisat: 2023), Departament de Física
Els continguts d'aquestes pàgines es poden usar sense modificar, retallar o refer amb finalitat educativa, sense ànim de lucre, citant l'autor de les pàgines i posant en lloc visible l'adreça d'aquest lloc web. Usau: "Exercicis d'Electromagnetisme· Antoni Amengual Colom · UIB url: http://dfs.uib.es/apl/aac/FGII23/".