Exercici 0
Camp elèctric: Llei de Gauss

Solució mostrar
El camp elèctric generat per càrregues distribuïdes cilíndricament és perpendicular a l'eix del cilindre i la seva intensitat només depèn de la distància a l'eix, tant a l'interior com a l'exterior del cilindre de plàstic.
Camp a l'exterior (r ≥ R)
A la Fig. 1, s'ha representat amb el color taronja una part del cilindre infinit on hi ha les càrregues i amb el color gris una superfície cilíndrica de radi r tancada i concèntrica amb l'anterior, a la qual s'aplicarà la llei de Gauss per calcular el camp elèctric a la distància r de l'eix del cilindre. El dibuix s'ha duplicat per il·lustrar que la direcció del camp en punts de la tapadora superior és paral·lela a la superfície i, per tant, perpendicular al vector normal 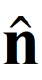 en cada punt (Fig. 1a) i en punts de la superfície lateral, el camp és perpendicular a la superfície i, per tant, paral·lel al vector normal
en cada punt (Fig. 1a) i en punts de la superfície lateral, el camp és perpendicular a la superfície i, per tant, paral·lel al vector normal 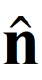 en cada punt (Fig. 1b).
en cada punt (Fig. 1b).
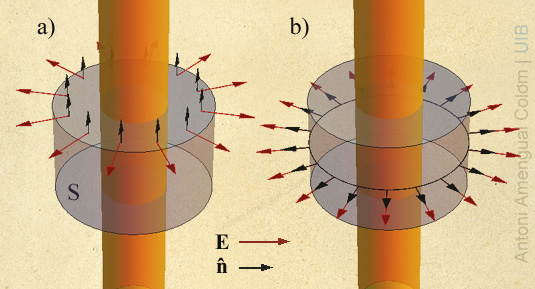
La superfície S de radi r a la que s'aplicarà la llei de Gauss té una tapadora superior, una tapadora inferior i el lateral. En els punts de les tapadores superior i inferior, el camp és horitzontal i el vector normal és perpendicular al camp, de manera que el producte escalar E·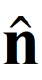 és zero: El flux de camp elèctric a través de les tapadores és zero.
és zero: El flux de camp elèctric a través de les tapadores és zero.
En els punts de la superfície lateral, el camp elèctric i el vector normal són paral·lels, de manera que
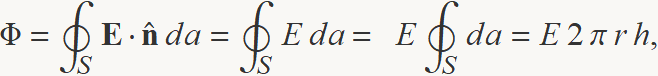
La càrrega tancada pel cilindre gris de radi r és tota la del cilindre de radi R i altura h,
qint = (π R2 h) ρ0.
Aplicant la llei de Gauss, es té
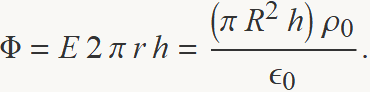
D'aquí, s'obté
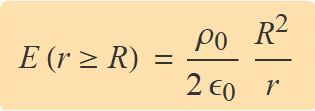
Camp a l'interior (r ≤ R)
Per calcular el camp a l'interior del cilindre de càrregues, s'ha de considerar una superfície cilíndrica concèntrica que queda dins el cilindre (Fig. 3). L'expressió del flux a través de la superfície és la mateixa Eq. (1).

La càrrega tancada per la superfície cilíndrica de radi r és
qint = (π r2 h) ρ0.
Aplicant la llei de Gauss, es té
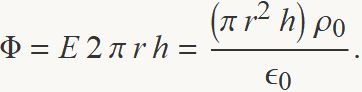
S'aïlla el camp d'aquesta equació i s'obté
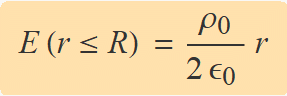


Text, gràfics i disseny d'aquest lloc web:
Antoni Amengual Colom (Revisat: 2023), Departament de Física

Els continguts d'aquestes pàgines es poden usar sense modificar, retallar o refer amb finalitat educativa, sense ànim de lucre, citant l'autor de les pàgines i posant en lloc visible l'adreça d'aquest lloc web. Usau: "Exercicis d'Electromagnetisme· Antoni Amengual Colom · UIB url: http://dfs.uib.es/apl/aac/FGII23/".
 Índex lista
Índex lista Exercici anterior
Exercici anterior Exercici posterior
Exercici posterior