Bloc E
Biga sobre dues columnes
- 1. Forces sobre la biga
- 1.1. Unitats de força
- 1.2. Exemple 1
- 1.3. Exemple 2
- 1.4. Exemple 3
Forces sobre la biga 

Ho has de saber
• Calcular les forces de dues columnes per suportar una biga horitzontal.
Només es consideraran els casos d'un biga de secció uniforme on el centre de la biga está entre les dues columnes.
Les forces de les columnes sobre la biga van cap a dalt.
El centre de gravetat d'una biga uniforme estarà en el centre geomètric. Quan la biga està sobre dues columnes amb el centre entre elles, pitja les columnes cap avall i les columnes fan dues forces de mòduls A i B cap a dalt sobre la biga. La suma d'aquestes dues forces és igual al pes P de la biga. L'equació de la suma forces és
A + B = P
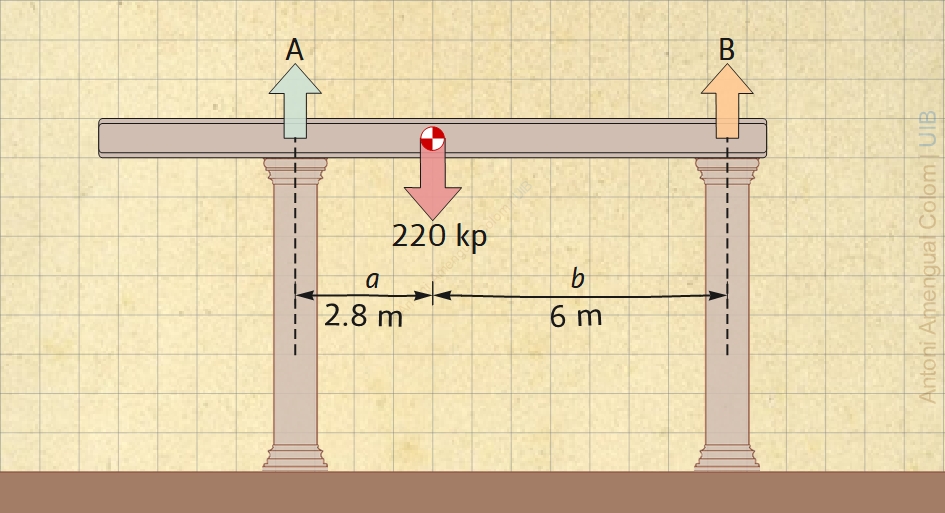
En equilibri la suma dels moments de les forces ha de ser zero. Siguin a i b les distàncies del centre de gravetat de la biga al centre de cada columna (Fig. 1).
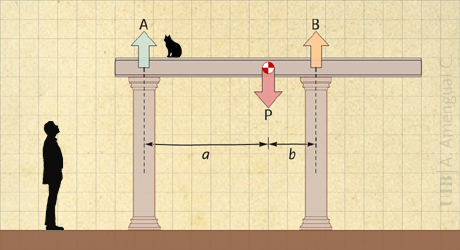
Els moments de les forces es poden calcular respecte de qualsevol punt. Convé calcular les forces respecte del punt superior d'una de les columnes, per exemple, la columna de l'esquerra, perquè el moment de la força A és zero. Així, l'equació de la suma de moments dona
(a + b) B = a P
Coneguts els valors d'a, b i el pes P de la biga, la segona equació permet determinar el valor de B. Després, l'equació de la suma de forces permet calcular A.
Unitats de força 

La unitat de força del Sistema Internacional d'Unitats és el Newton (símbol N).
El quilogram-força o quilopond (símbol kp) és útil quan la força resistent R és el pes d'un objecte.
El pes d'un objecte en newtons és la massa de l'objecte multiplicada per l'acceleració de la gravetat (g = 9.8 m/s2).
Una pesa de 10 kg penjada d'una barra com a la Fig. 2 fa una força sobre la barra de 10 kp o 98 N.
Exemple 1 

Resolució mostrar
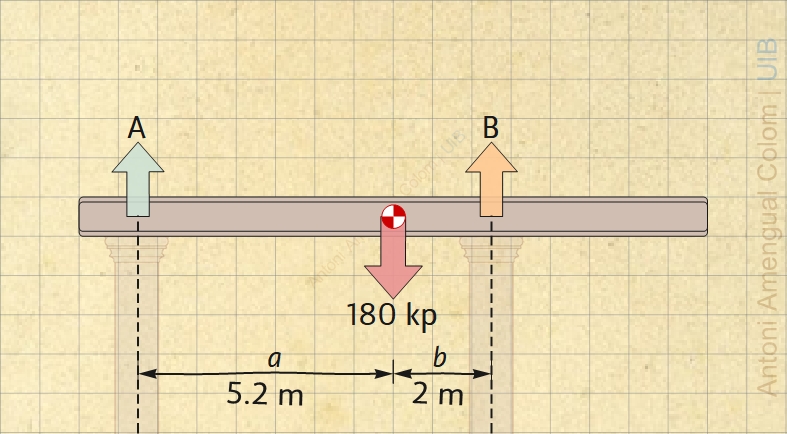
Calcula les forces que fan les columnes sobre la biga representada a la Fig. 3.
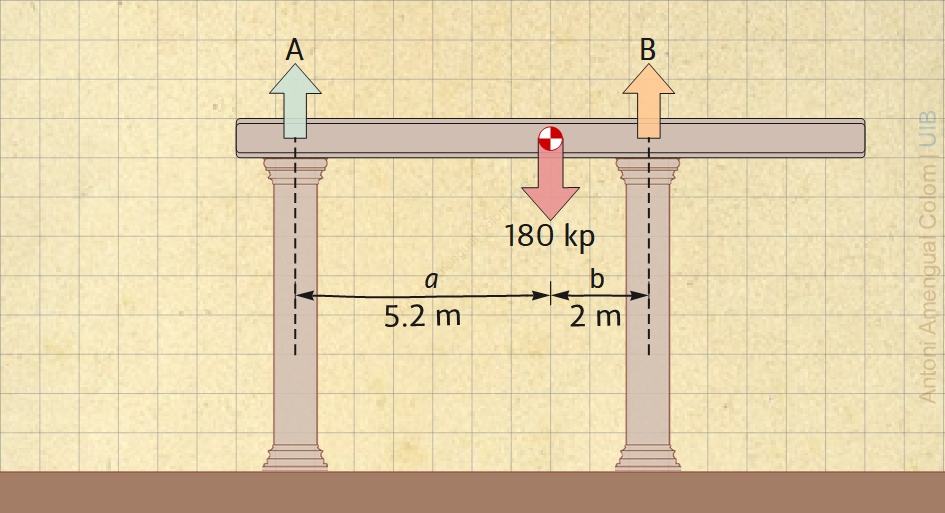
Exemple 2 

Resolució mostrar
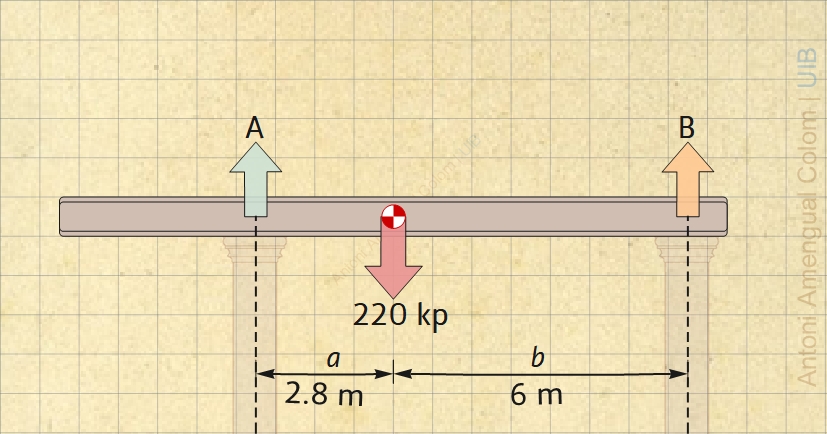
Calcula les forces que fan les columnes sobre la biga representada a la Fig. 3.
Exemple 3 

Resolució mostrar
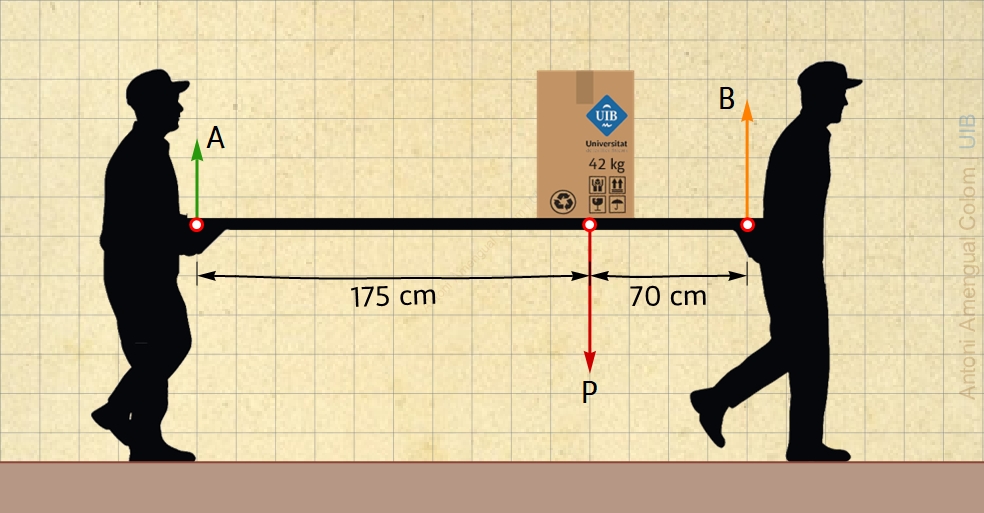
De manera semblant a com es calcula la força que fan dues columnes sobre una biga, es pot calcular el pes que suporta amb les mans cada treballador quan els dos duen una caixa de 42 kg com mostra la Fig. 6.


 Portada
Portada Índex temes
Índex temes