Bloc E
Les palanques
Ho has de saber
• Conèixer que hi ha tres tipus de palanques.
• Saber definir i identificar cada tipus de palanca.
• Saber calcular la força que s’ha d’aplicar en cada un dels tipus de palanques perquè la palanca es trobi en equilibri.
Què és una palanca? 

Una palanca és una màquina simple.
Es denomina màquina simple al dispositiu que, a partir de l'aplicació d'una força i amb un desplaçament, produeix una altra força amb un desplaçament diferent.
Una corriola també és una màquina simple: S'estira una corda que passa per la corriola cap avall i el que hi ha a l'altra extrem de la corda, puja.
La palanca és, essencialment, una barra rígida que es recolza i pot girar sobre un punt denominat fulcre, i transmet la força aplicada a un altre punt de la barra.

La invenció de la palanca s'atribueix a Arquimedes de Siracusa que visqué aproximadament entre el 287 i el 212 a. C.
L'urpa d'Arquimedes va ser dissenyada per defensar la murada marítima de Siracusa durant el setge de la ciutat per part de la flota de la República romana entre els anys 213 i 211 a. C. Els relats dels historiadors antics descriuen l'urpa com una palanca amb ganxos metàl·lics a l'extrem extern per enganxar la proa de la nau atacant. Una vegada enganxada la proa, s'estirava de l'altre extrem de la palanca per avall i la proa del vaixell s'elevava. Llavors, es deixava caure el vaixell el qual s'escorava o s'enfonsava. A la figura següent, la barra rígida s'ha dibuixat de color vermell.
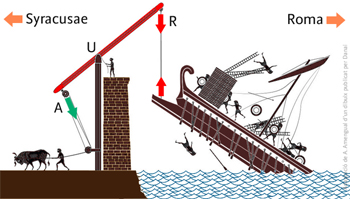
La fletxa vermella de la figura que apunta cap a dalt representa la força que fa la corda estirant de l'esperó a la proa del vaixell. La fletxa vermella que apunta cap a baix, representa la força que fa la mateixa corda estirant de l'extrem extern de la palanca. La fletxa verda representa la força que s'ha de fer en el costat de la palanca dins la murada.
Els tres tipus de palanques. 

S'identifiquen tres forces actuant sobre la barra de la palanca que s'anomenen força aplicada A, força resistent R i força del fulcre U i el tipus de palanca queda identificat per quina de les tres forces està entre les altres dues (Fig. 1).

Cal tenir present que el sentit de la força aplicada no canvia el tipus de palanca. Per exemple, si en lloc del pes hi hagués una molla comprimida entre la barra de la palanca i la base, els sentits de totes les forces serien els contraris dels que tenen les forces en el cas de la Fig. 1.
A continuació es descriu un exemple de cada tipus de palanca.
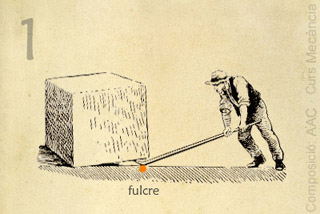
Palanca de primer ordre
La força U està entre les altres dues.
Exemple: La barra de la Fig. 2.

Palanca de segon ordre
La força R està entre les altres dues.
Exemple: Carretó. Encara que no sigui només una barra, un carretó és una palanca de segon ordre: El fulcre és l'eix de la roda; la força resistent és el pes del que hi ha dins la caixa; i la força aplicada és la feta en els mànecs.
En la primera menció a un carretó, es relata que el general Zhuge Liang (c.a. s. III a. C.) necessitava transportar equipament i armes per un camí de muntanya molt estret pel qual no hi passaven els carros de dues rodes. Per resoldre el problema del transport per aquells camins s'inventà un carretó d'una roda.
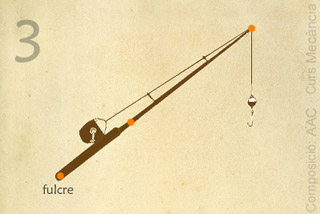
Palanca de tercer ordre
La força A queda està les altres dues.
Exemple: Canya de pescar peixos grans. El fulcre és l'extrem inferior de la canya que es posa dins la cavitat del cinturó. La força aplicada amb les mans queda enmig de la canya. La força resistent serà la que s'ha de vèncer si pica algun peix.
Forces sobre la barra horitzontal d'una palanca en equilibri 

Només es consideraran els casos on es compleix que:
− La barra de la palanca està horitzontal
− Les forces són perpendiculars a la barra de la palanca
− Cada una de les forces A, R i U es pot considerar aplicada en un punt de la barra
− Es coneix el valor i el sentit de la força aplicada A o de la força resistent R
− La barra serà de pes negligible o serà uniforme. En aquest segon cas, el problema es tracta considerant una quarta força P sobre la barra actuant en el punt central de la barra.
Unitats de força 

La unitat de força del Sistema Internacional d'Unitats és el Newton (símbol N).
El quilogram-força o quilopond (símbol kp) és útil quan la força resistent R és el pes d'un objecte.
El pes d'un objecte en newtons és la massa de l'objecte multiplicada per l'acceleració de la gravetat (g = 9.8 m/s2).
Una pesa de 10 kg penjada d'una barra com a la Fig. 1 fa una força sobre la barra de 10 kp o 98 N.
Criteris de signes 

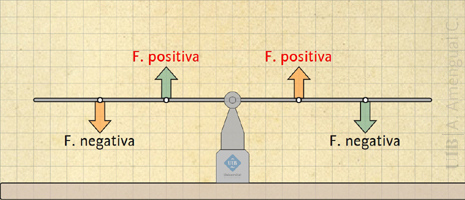
Els valors numèrics de les forces A, R, U són positius si les forces van cap a dalt i negatius, si van cap a baix (Fig. 5). El pes de la barra sempre va a baix i restarà.
El moment d'una força sobre la palanca és el producte de la força multiplicada per la distància del fulcre al punt d'aplicació de la força.
El d'un moment de força es defineix com es mostra a la Fig. 6 per als quatre casos possibles. Per recordar si el moment d'una força se suma o es resta a l'equació dels moments, el millor és pensar si una força, en absència de les altres, faria girar la barra en sentit antihorari (el moment se suma) o en sentit horari (el moment es resta).
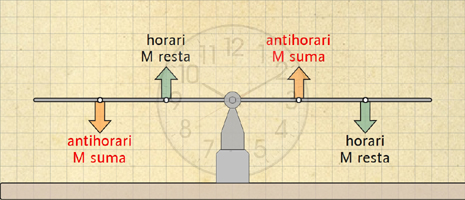
Les dues equacions per trobar les forces sobre la barra 

En general, les quatre forces esmentades, A, R, U i P, actuaran sobre la barra de la palanca.
Amb relació als moments:
La força U no generarà cap moment de gir.
El pes P de la barra no genera cap moment de gir només si la barra està centrada.
En general hi haurà tres moments de força respecte del fulcre.
Equació de la suma dels moments
Siguin a i r les distàncies del fulcre als punts d'aplicació de les forces A i R, respectivament.
Sigui p la distància del centre de la barra al fulcre.
Els moments de les forces seran a A, r R i p P. Cada moment se suma o resta amb la regla del sentit de gir horari o antihorari de la Fig. 6.
Suma dels moments = 0.
D'aquesta equació s'aïllarà la força desconeguda.
Equació de la suma de les forces
De manera general, s'escriurà
A + R + U + P = 0,
sense oblidar que els valors numèrics de les forces conegudes han de ser positius si les forces van cap a dalt i negatius si van cap a baix.
En molts de casos es pot saber el sentit de la força desconeguda. Si el sentit assumit no fos correcte, s'obtendria un valor negatiu de la força.
Exemple 1 

Resolució mostrar
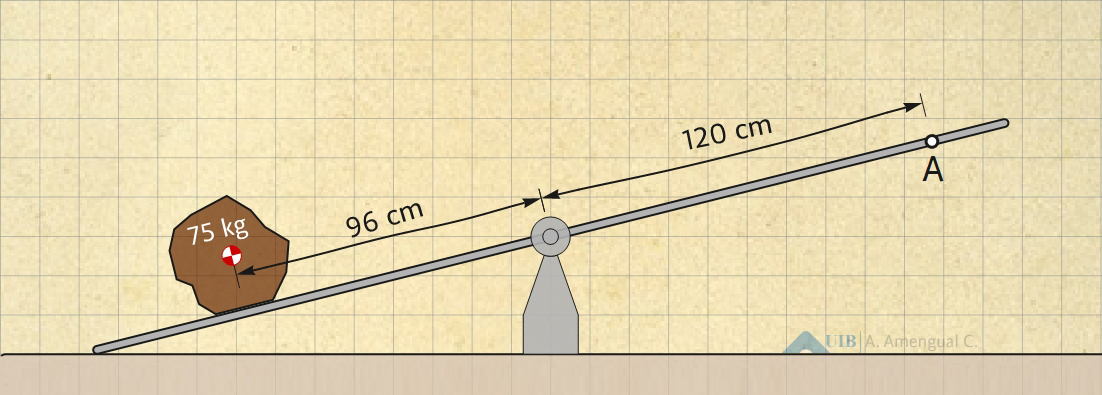
Quin tipus de palanca és la mostrada a la Fig. 7?
Quina força A perpendicular a la barra s'ha d'aplicar a la palanca de la Fig. 7 perquè la barra es mantingui horitzontal?
Quina força U fa el fulcre sobre la barra si el pes d'aquesta és negligible?
Exemple 2 

Resolució mostrar
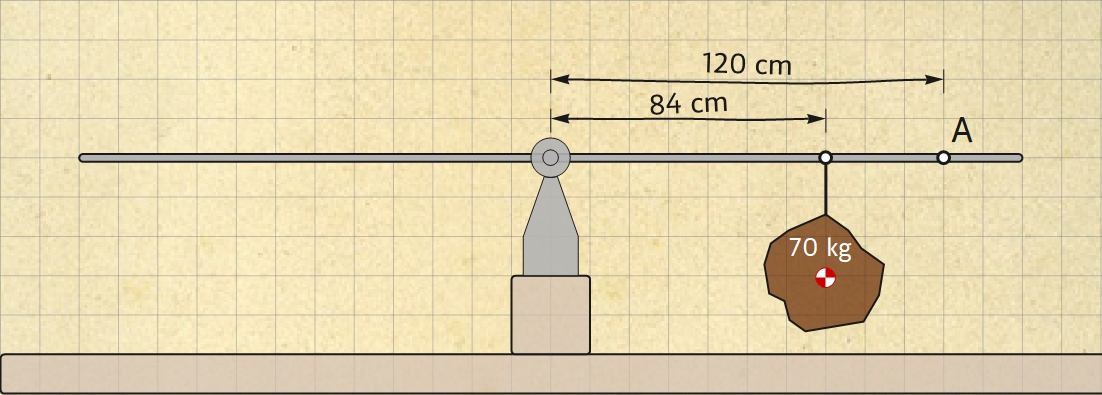
Quin tipus de palanca és la mostrada a la Fig. 8?
Quina força A perpendicular a la barra s'ha d'aplicar a la palanca de la Fig. 8 perquè la barra es mantingui horitzontal?
Quina força U en newtons fa el fulcre sobre la barra?
Exemple 3 

Resolució mostrar
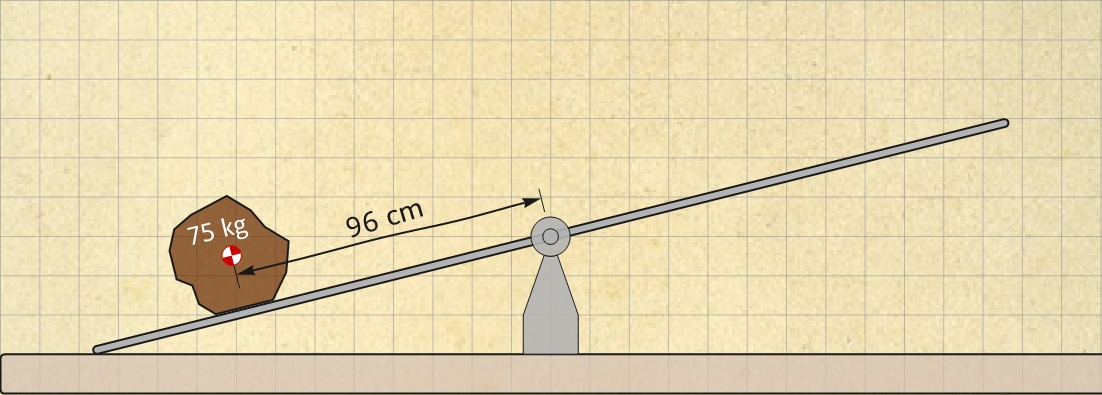
S'aplica una força de 1960 N per mantenir la barra de la palanca de la Fig. 9 horitzontal. Si es tracta d'una palanca de tercer ordre, el punt d'aplicació de la força està a l'esquerra o a la dreta del fulcre?
A quina distància del fulcre s'aplica la força?
Quina força U en quiloponds fa el fulcre sobre la barra? En quin sentit?
Exemple 4 

Resolució mostrar
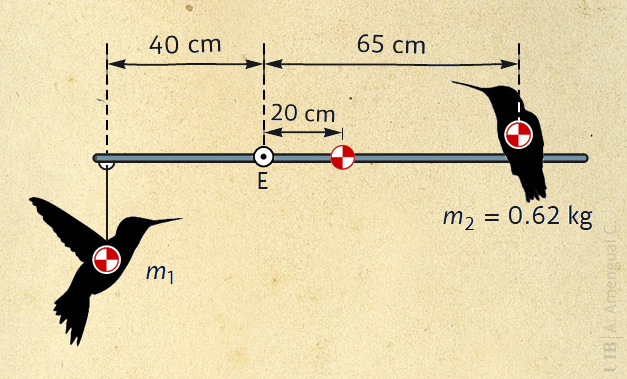
Dues figures amb forma d'ocells com mostra la Fig. 10 estan en equilibri en una barra que pot girar lliurament al voltat de l'eix E perpendicular al pla del dibuix. Quina massa m1 ha de tenir la figura de l'ocell esquerra per mantenir la barra horitzontal en equilibri si la barra de la massa és:
a) Negligible.
b) 0.50 kg.


 Portada
Portada Índex temes
Índex temes