Bloc E
Les lleis de Kepler
Ho has de saber
• Saber enunciar les tres lleis de Kepler
• Conèixer el concepte de velocitat areolar
• Saber usar la tercera llei de Kepler en el nostre sistema solar usant com a unitats anys i unitats astronòmiques
Què són les lleis de Kepler? 


Les lleis de Kepler són tres lleis enunciades per l'astrònom Johannes Kepler (1571-1630) que descriuen el moviment dels planetes al voltant del Sol.
Aquestes lleis són fonamentals en l'astronomia i han estat clau per comprendre el sistema solar.
Les lleis es varen deduir per al sistema solar però són aplicables al moviment a qualsevol estrella que tengui planetes al seu voltant i a les llunes d'un planeta gran.
Primera llei o llei de les òrbites 

La primera llei de Kepler estableix que tots els planetes es mouen al voltant del Sol en òrbites el·líptiques, amb el Sol ubicat en un dels focus de l'el·lipse.
Segona llei o llei de les àrees 

La segona llei de Kepler estableix que la línia imaginària des del Sol al planeta escombra àrees iguals en intervals de temps iguals.
La velocitat areolar d'un planeta és l'àrea escombrada per la línia imaginària des el Sol al planeta en la unitat de temps. En termes d'aquesta velocitat, la segon llei de Kepler estableix que la velocitat areolar d'un planeta és constant.
Aquesta llei està il·lustrada a la Fig. 2. Les tres zones de color verd tenen la mateixa àrea. El planeta representat pel punt blanc empra el mateix temps per anar del punt A al B, del C al D i de l'E a l'F.
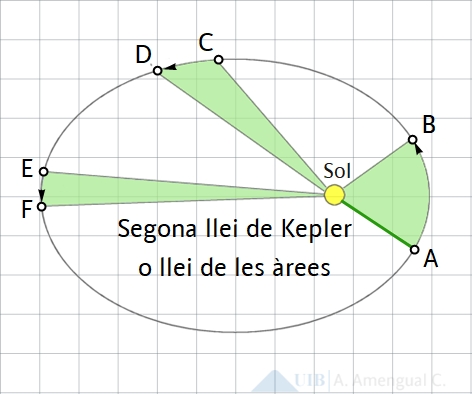
El fet que un planeta escombri àrees iguals en períodes de temps iguals i l'òrbita sigui el·líptica significa que la velocitat del planeta varia al llarg de l'òrbita. La distància recorreguda pel planeta entre A i B és més gran que entre E i F, per tant, el planeta es mou més ràpid entre A i B (quan està més a prop del Sol) que entre E i F (quan està més lluny). La velocitat del planeta canvia contínuament. L'animació de la Fig. 3 il·lustra el canvi de la velocitat al llarg de l'òrbita.

Es denomina periheli al punt de l'òrbita d'un planeta més a prop del Sol, i afeli, al punt més llunyà. Està demostrat que el producte de la velocitat i la distància al Sol quan el planeta passa pel periheli és igual al mateix producte quan el planeta passa per l'afeli. Matemàticament,
rp vp = ra va,
on rp i vp són la distància al Sol i la velocitat del planeta quan passa pel periheli i ra i va, quan passa per l'afeli.
La Terra passa pel periheli a principi d'any (en el 2024, el 5 de gener) i, per l'afeli, a principi de juliol (en el 2024, el 6 de juliol). Amb les dades següents, comprovau que la velocitat de la Terra quan passa per l'afeli es 1 km/s més lenta que quan passa pel periheli:
Periheli Terra: rp = 147.1 106 km, vp = 30.29 km/s.
Afeli Terra: rp = 152.1 106 km, va = ?
Tercera llei o llei dels períodes 

La tercera llei de Kepler estableix que el quadrat del període orbital d'un planeta és proporcional al cub del semieix gran de l'òrbita del planeta.
Matemàticament, se sol expressar la llei escrivint que el quocient entre el període T al quadrat i el semieix gran al cub és constant
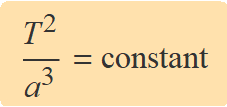
Aplicació al Sistema solar 
Si s'usa l'any com a unitat per mesurar els períodes i la unitat astronòmica, per mesurar la mida dels semieixos de les òrbites, resulta que la constant per al sistema solar val 1 perquè,
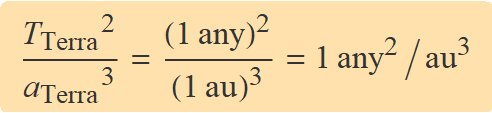
A la Taula següent es presenten els períodes orbitals i els semieixos grans de les òrbites dels planetes del sistema solar. Calculau T2 / a3 per a cada un dels planetes per comprovar el compliment de la tercera llei de Kepler. El càlcul dels valors de la tercera columna de la taula donarà 1 amb bona aproximació però no exactament: La tercera llei de Kepler es determina suposant que no hi ha interacció gravitatòria entre els planetes, quan aquesta existeix.
| Planeta | T (any) | a (ua) | T2 / a3 |
| Mercuri | 0.241 | 0.3871 | |
| Venus | 0.615 | 0.7233 | |
| Terra | 1 | 1.00 | 1.00 |
| Mart | 1.88 | 1.524 | |
| Júpiter | 11.86 | 5.204 | |
| Saturn | 29.46 | 9.582 | |
| Urà | 84.01 | 19.229 | |
| Neptú | 164.8 | 30.104 |
Aplicació a les llunes de Júpiter 
La tercera llei de Kepler es pot aplicar als planetes nans i també es pot aplicar a les llunes d'un planeta, especialment quan el planeta es gran, com és el cas de Júpiter. T2 / a3 serà una nova constant per a les llunes de Júpiter.
Galileu va ser el primer en veure que Júpiter tenia satèl·lits al 1609. Amb el seu telescopi recentment construït, va descobrir l'existència de quatre llunes: Io, Europa, Ganimedes i Cal·listo (Fig. 4) . Actualment, s'han registrat ja més 90 satèl·lits naturals de Júpiter (com més petits són, més s'ha tardat en observar-los).

Els períodes orbitals i els semieixos de les òrbites de les llunes que descobrí Galileu es presenten a la taula següent. Calculau T2 / a3 per a cada una de les llunes i comprovau el compliment de la tercera llei de Kepler.
| Lluna | T (dies) | a (km) | T2 / a3 |
| Io | 1.7691 | 421600 | |
| Europa | 3.5512 | 671100 | |
| Ganimedes | 7.1546 | 1070400 | |
| Cal·listo | 16.689 | 1882700 |
Els quatre valors de T2 / a3 se semblen molt. Per quantificar-ho, calculau la mitjana M dels quatre valors i, després, calculau per a cada lluna
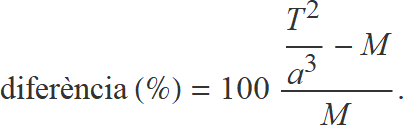
Comprovau que la diferència màxima no arriba al 0.06 %.


 Portada
Portada Índex temes
Índex temes