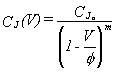EL
TRANSISTOR BIPOLAR (BJT) EN SPICE
1. INTRODUCCIÓ
En el present capítol l´objectiu és
presentar els paràmetres que permeten la modelització del transistor bipolar en
el programa PSPICE, i conèixer una sèrie de mètodes per a la seva extracció. En
primer lloc es farà una petita introducció a la física del transistor bipolar
on es presentarà el concepte de l’efecte transistor i del paràmetre b del transistor, i es comentaran
els diferents modes de funcionament, després es tractarà els models elèctrics que
són la base per a la modelització del transistor bipolar i que ens portarà a la
modelització PSPICE, i seguidament es fa una presentació dels principals
paràmetres associats. Finalment s’haurà d’estudiar l’ extracció d’aquests
paràmetres.
1.1 Física del transistor bipolar: l’ efecte transistor i
modes de funcionament.
La unió PN és la base fonamental
per comprender el transistor bipolar. Aquest no és més que la unió de dues
unios PN enfrontades: NP i PN ( per al
cas d’un transistor NPN) o de dues PN i NP (per al cas d’un transistor PNP). Al
llarg de tot el present capítol ens referirem als transistors NPN.
Les tres regions del transistor són: a)
la regió més dopada N+ (P+) anomenada emissor, b) la
regió del mig estreta i amb un dopatge gradual que és la base tipus (P) , i c)
la darrera regió que és més llarga i amb un dopatge baix que és el col.lector
(N-). Una representació d’un transistor bipolar N+PN-
es té a la figura 1.1. El mode de funcionament o d’operació més normal per un
transistor és quan es diu que està treballant en mode actiu directe. Això vol
dir que la unió PN ( base-emissor) està en directe i la unió PN
(base-col.lector) està polaritzada en inversa. A la figura 1.2 es representa el
diagrama de bandes d’energia per la situació en què es té al transistor en
equilibri i polaritzat en directe.
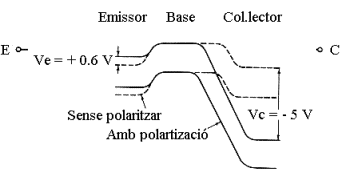
Figura 1.1: Tall transversal d’un
transistor NPN.
Figura 1.2: Diagrama de les
bandes d’energia.
Com en el cas d’una unió PN simple, la
unió base-emissor si està polaritzada en directe (VBE > 0 ) fa que
l’alçada de barrera de construcció de la unió disminueixi i que la unió
base-col.lector polaritzada en inversa faci que l’alçada de barrera augmenti
amb la tensió inversa ( VBC < 0 ).
Així
doncs si es té la unió BE en directe es té una injecció de forats de la base
cap a l’emissor ( corrent IpE ) i un corrent d’electrons injectats
de l’emissor cap a la base (corrent InE ). Aquests electrons
injectats a la base són portadors minoritaris i estaran sotmesos a
recombinacions. Però la base és prou curta com per a que gran part dels
electrons injectats sobrevisquin i arribin al col.lector. Quan arriban veuen el
cap elèctric que hi ha en aquesta regió i es veuen escombrats (corrent IC
n ). Això implica que per a la unió que està en inversa pot passar un
nivell de corrent superior que si estigués la unió aïllada. Aquesta és la base
de l’efecte transistor, que es té sempre que les dues unions estiguin prou
properes.
A la figura 1.3 es representen els
corrents dins del transistor. La diferència entre InE i InC
són els forats injectats pel corrent de base per recombinar-se amb els
electrons a la regió de la base.
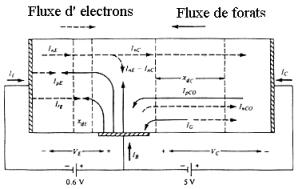
Figura 1.3: Components de
corrents dins del transistor bipolar. En realitat es representen
els sentits que del fluxe dels
portadors. El sentit dels corrents dels electrons és l’oposat al dibuixat.
Les
altres components representades són: I r g que representa el corrent
de recombinació a la zona de deplexió de la unió base-emissor, IG és
el corrent de generació de portadors a la unió base-col.lector, i In CO
i Ip CO representen els corrents de saturació en inversa de la unió
base-col.lector. Aquest tres darrers corrents són prou petits i es combinen en
el corrent designat per ICO anomenat corrent de saturació en inversa
del col.lector.
A
continuació s’introduirà el concepte del guany b del transistor bipolar. Per fer això en primer lloc cal definir el
guany de corrent a:
aquestcoeficient és la relació del corrent de sortida respecte el corrent
d’entrada. Segons la figura 1.3, l’ entrada és l’ emissor i la sortida és el
col.lector. En aquesta situació es diu qu es treballa en la configuració de
base comuna. El coeficient a és defineix com:
a º IC – I CO / I E
(1.1)
Si es té present la figura 1.3, es poden
escriure les següents expressions:
IE+IC+IB
= 0 (1.2)
-IE= I pE+ I rg + I nE (1.3)
IB = I pE + I rg + ( I nE - I nC) -ICO (1.4)
IC = I nC + ICO (1.5)
Fent servir aquestes equacions s’arriba a:
a = I nC / ( I nE + I pE + I rg ) = g bT
(1.6)
on g és l’eficiència d’injecció de l’emissor
i bT és el factor de transport a la base, que
són:
g = I nE / ( I nE + I pE + I rg ) (1.7)
bT = I nC / I nE (1.8)
El
coeficient g representa la proporció de portadors
minoritaris que arriban a la base. Els components I pE + I rg no contribueixen i s’han de
minimitzar als màxim. El coeficient bT la proporció dels portadors minoritaris
injectats que després de les recombinacions arribaran al col.lector. Aquests
dos coeficients són inferiors a la unitat i això fa que a<1, però per als transistors
bipolars ben dissenyats aquest paràmetre serà molt proper. Si es re-escriu
l’equació 1.1, es té
IC = - a IE + I CO
(1.9)
i amb aquesta equació 1.9 amb l’equació
1.2 pot expressar-se no en funció del corrent d’emissor sino en funció del corrent
de base i arribar a
IC = (a/1-a) * IB + I CO/
(1- a ) = b IB + ICEO
On b és el guany de corrent per a la
configuració emissor-comú.
Ara
es té una visió una mica general del funcionament del transistor i dels seus
corrents. Cal fer una descripció a continuació dels diferents modes de treball
en què es pot trobar el transistor. A la figura 1.4 es representen els quatre
possibles modes de funcionament: a) el mode actiu directe ( VBE >
0 i VBC < 0 ), b) el mode actiu invers ( VBE < 0 i VBC > 0 ), c) saturació (
VBE > 0 i VBC > 0 ), i d) tall ( VBE
< 0 i VBC < 0 ).
Figura 1.4: regions de treball del transistor.
El següent pas , després de
conèixer una mica la física i funcionament del transistor, és passar ja a
conéixer com es modelitza el dispositiu elèctricament.
1.2 Modelització del transistor
bipolar.
Primerament es presentarà el model
d’ Ebers-Moll per a les seves dues versions: a) el model d’ injecció i b) el
model de transport. Aquestes dues versions es basen en les mateixes equacions,
però la segona és la que es fa servir com base per a la modelització del
comportament del transistor bipolar (BJT) mitjantçant PSPICE. Presentat el
model d’Ebers-Moll per a PSPICE, analitzarem el model complexe de Gummel-Poon.
Aquest model considera efectes que no són considerats en la versió ideal
d’Ebers-Moll i que agafant la versió del model de transport fent una sèrie de
modificacions i afegits serà el model que és implementat en el simulador.
1.2.1
Model
d´Ebers-Moll
Donada la resolució de l´equació de
continuïtat amb les condicions de contorn necessàries, i amb les aproximacions
de buidament de portadors, de considerar com inexistents els efectes de
generació i recombinació a les ZCE, de menysprear els efectes de recombinació
superficials, i que el corrent és unidireccional, es podran trobar unes expressions per als corrents de col.lector,
emissor i base per al transistor, però aquest no és l’objectiu del present
treball. En tot cas les solucions són les donades a l’ equació 1.10.
Equació 1.10: Solució dels corrents
d’un transistor NPN en base a la equació de continuïtat.
Però també es pot fer una deducció molt més ràpida i
intuïtiva dels corrents del transistor. Es poden separar els corrents en dos components. El primer, és el corrent
degut a l´efecte transistor. El segon
terme és el corrent de la unió, és a dir, del diode, sigui la unió emissor-base
o base-col.lector. Així doncs es pot arribar a escriure
|
|
Equació 1.2: Model d’injecció.
Aquest és l´ anomenat model estàtic
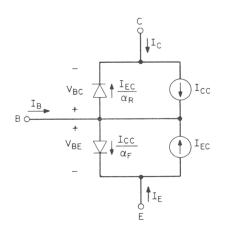
d'Ebers-Moll, versió d'injecció. El model es representa a la figura 1.5.
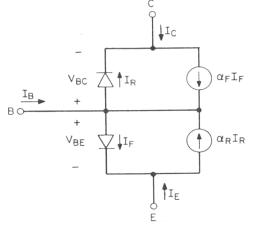
Fig.1.5:
Model Ebers Moll estàtic. Versió Injecció.
aF i aR són els guanys de senyal gran,
quan el transistor treballa en mode actiu directe i mode actiu invers
respectivament, i representen les fraccions de corrent de IF(IR)
que arriben al col.lector (emissor). Aquest mateix model podem transformar-lo
matemàticament i arribar a la versió del Transport.
Les expressions calculades amb les
intuïtives volen descriure el mateix. Això implica que si es té en compte que a12=a21,
alehores (eq.1.11)
|
|
Equació 1.11: Corrent de saturació del transistor.
que es coneix també com relació de reciprocitat.
Aquestes porcions dels corrents en
inversa de les unions EB i BC, defineixen el corrent IS, (el corrent
de saturació en inversa del BJT). Aleshores, definida IS, es poden definir unes fonts de corrent que
representen els corrents deguts a l´efecte transistor com
|
|
Equació 1.12: Fonts de corrent
de forma que els corrents de
col.lector i emissor els podem escriure
|
|
Equació 1.13: Equacions per al model de transport.
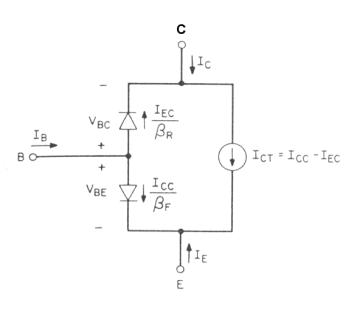
El model seria el representat a la figura 1.6.
|
|
Fig.1.6:
Versió Transport.
Però
encara podrà fer-se una altra modificació, i és la que farà servir PSPICE, i és
definir una única font de corrent ICT entre emissor i col.lector,
per substituir les fonts de corrent ICC i IEC. Així
doncs, el model Ebers-Moll per SPICE és el representat a la figura 1.7.
L´expressió del corrent ICT és
|
|
Equació 1.14: Corrent ICT.
aquesta expressió es farà servir més endavant quan es
tracti, dins del model de Gummel-Poon, com poden ésser modelitzats alguns
efectes de gran importància que no els considera el present model.
|
|
Fig1.7:
Model SPICE Ebers-Moll.
Si es tenen presents les següents expressions 
i 
es podrà
escriure doncs
(1.15
)
Aquestes
equacions ( eq.1.15) són la base que pren el model de Gummel-Poon i és el que
serà implementat en el simulador elèctric PSPICE. En tot cas, com a resum,
caldrà que es tinguin presents les equacions 1.15 i 1.14.
Fins aquí, els paràmetres que
permeten fer una modelització del dispositiu són: a) IS (IS), que és
el corrent invers de saturació, b) bF
(BF), que és el guany ideal màxim del corrent en el mode actiu durecte, i c) bR
(BR), que és el guany ideal màxim del corrent en el mode actiu invers.
1.2.2 Model de Gummel-Poon
El model d’ Ebbers-Moll és una
primera aproximació que preten modelitzar el comportament elèctric del
transistor bipolar. Aquest no considera tot un conjunt d’efectes de segon
ordre que són molt importants. Aquests efectes són principalment, els de baixa
i alta injecció i els efectes de modulació de la llargada elèctrica de la Base;
és a dir, els efectes de generació-recombinació a les zones de deplexió, i els
efectes de variació de l’amplada
efectiva de la base en funció de les variacions de les amplades de les zones de deplexió que
depenen dels nivells de polarització de les unions.
A grans trets els efectes
a modelitzar són:
·
Els efectes de baixa injecció que són aquells que estan relacionats amb el
fet de que la recombinació-generació de portadors a les ZCE de les unions
base-emissor i base-col.lector fan aparèixer uns corrents que no són
menyspreables a baixos nivells de polarització.
·
Els efectes d' alta injecció que són aquells que estan associats al fet de
que quan el nivell d´injecció de portadors a la base és gran, la variació de la
càrrega dels majoritaris ja no pot ésser menyspreada.
·
Finalment, l´efecte de modulació de l´amplitud de la base. Com més gran
sigui la polarització en inversa de la unió BC quan tenim el transistor
treballant en mode directe, l´amplada elèctrica de la base serà més petita que
la seva llargada física. Això fa que el corrent de col.lector a la zona activa
no sigui constant, sinó que vagi augmentant amb la polarització.
Es veurà que la modelització dels
efectes de baixa injecció són fàcilment modelitzables i que els altres dos
vindran modelitzats directament quan s’introdueix el concepte de càrrega de
majoritaris a la base QB i la seva dependència amb la polarització.
1.2.2.1 La variació del guany de corrent b amb el corrent. Els efectes de
baixa injecció.
Són tres les regions (Fig.1.8.) que
es poden distingir quan representem el guany b en funció del nivell de corrent
(per VBC=0). La primera
regió és la que tes té per baixos nivells de corrent, quan el guany està
degradat pel fet de que es tenen uns components de més que en el corrent de
base. La segona regió és per corrents mitjos, on es defineix un valor constant bFM. La regió tres és per als nivells d’alta injecció, lligats als canvis
per al corrent de col.lector.
Fig.1.8: bF vs. IC .
Si es considera que el
transistor treballa en mode actiu directe i que VBC=0, es té que:
a)
Per als nivells de corrents mitjos:
aquesta seria la regió ideal on les equacions trobades en la modelització d’
Ebbers-Moll són correctes. Amb la condició de VBC=0 les equacions
que descriuen els corrents de col.lector i base serien ( eq. 1.16):
IC
= IS ( exp (q VBE / KT) –1 )
IB= ( IS
/ bf
) * (exp (q VBE / KT) –1 ) (1.16)
b)
Per als nivells baixos de corrent: es
conegut, des de la pràctica del diode, que per baixos nivells de conducció són predominants
els corrents originats per recombinació respecte els de difusió. Aquests
corrents de recombinació estan principalment lligats a la recombinació
mitjantçant centres de generació-recombinació (Recombinació
Shockley-Read-Hall), on aquest corrent era descrit mitjantçant una equació del
tipus expressat a l’equació 1.17, on n @ 2.
(1.17)
Pel BJT es té que per baixos nivells de conducció es tenen nivells de corrent adicionals que estan relacionats als corrents de recombinació a la ZCE (zona de deplexió) de la unió BE (quan es té el transistor en mode actiu directe), a corrents de recombinació a la ZCE de la unió BC (quan es té el transistor en mode actiu invers), a corrents de recombinació de portadors a la superfície, etc.
En el cas on VBC=0, i el transistor en mode actiu directe
(junció BE en directe), aquests corrents podem representar-se en la forma,
(equació 1.18 )
(
1.18 )
on s’ha definit un nou paràmetre, NE
( coeficient d´emissió BE no ideal per baixos nivells de corrent ) i el
corrrent ISE. En el cas en què el transistor estigui funcionant en
el mode actiu invers es té una expressió semblant a la donada en l’equació
1.18, però es defineixen altres dos paràmetres: el coeficent NC
(coeficient d´emissió BC no ideal per baixos nivells de corrent ) i el corrent
ISC.
L’ expressió del corrent IB serà ara per al cas en què
es treballi en el mode actiu directe, si afegim aquest corrent ( equació 1.19 )
( 1.19 )
En el cas on VBE=0, i el transistor en mode actiu invers (junció
BC en directe), es té, de forma anàloga, un corrent de base (equació 1.20 )
( 1.20 )
Així doncs, el corrent de base
total és la suma de les equacions 1.19 i 1.20 (equació 1.21 )
+ 
(1.21)
Es pot ara retornar al model d’
Ebbers-Moll representat a la figura 1.7 i modelitzar aquests nous corrents, que
modelitzen els efectes de recombinació-generació a les zones de deplexió,
mitjantçant dos diodes. A la figura 1.9
es representa el nou esquema del model elèctric del transistor, però ara ja és
el model de Gummel-Poon .
Ara el corrent de col.lector serà el
donat a l’equació 1.22:
( 1.22 )
Arribats
aquí es tenen quatre paràmetres nous afegits per tal de modelitzar els efectes
dels corrents de generació-recombinació a les zones de deplexió i són: ISE
, ISC , NE i NC .
1.2.2.2 El concepte de QB : els efectes d’ alta injecció i modulació
de l’amplada de base.
Fins
ara s’ha presentat com es pot modelitzar el comportament elèctric del
transistor bipolar quan treballa en la regió de corrents mitjos i per als
baixos nivells de corrent. Per poder modelitzar el comportament del transistor
per alts nivells de corrent i els efectes de modulació de l’amplada de la base,
és necessari introduir dues coses: a) el fet que el corrent IS en
realitat no és constant i b) el concepte de la càrrega de majoritaris a la base
QB.
1.2.2.2.1 El paràmetre IS .
Si el
transistor bipolar treballa en el mode actiu directe i es té present la figura 1.3 i les equacions de g
( l’eficiència d’injecció de l’emissor ) i bT ( el factor de transport a la base ) i
aquests són pràcticament la unitat, el
fluxe de forats que es té a les unions emissor-base i base-col.lecor
serà molt petit i es podrà agafar com zero.
|
|
(1.23)
Donades les expressions del les
densitats de corrent ( equacions 1.23 )
amb Jp=0 es pot trobar
una expressió (equació 1.24) per al
camp elèctric E(x) . Això serà cert sempre que estem a la zona activa i lluny
dels efectes d'alta injecció.
(1.24) 
aquesta expressió es fa servir a Jn(x).
Aleshores, si es fa el producte Jn(x)*p(x), i es fa servir la regla
de la derivació d'un producte i les relacions d'Einstein, es pot arribar a
l’expressió (equació 1.25)
(1.25)
Com els efectes de recombinació-generació
es poden estudiar i modelitzar per separat no els considerem aquí i es pren Jn
constant. De fet, aquests efectes els podem desacoplar per considerar Jn
constant ja que els podem simular mitjantçant uns diodes no lineals, com s’ha
vist. El següent pas és integrat aquesta expressió (equació 1.25 ). Els límits
d’integració es representen a la figura 1.10.
Es té aleshores la següent expressió
(equació 1.26)
(1.26)
Si
es fa servir la relació que es diu que el producte pn a les fronteres està
relacionat amb el voltatge a les unions (equació 1.27)
|
|
( 1. 27 )
S’arriba a la següent expressió per a la densitat de
corrent Jn (equació 1.28 ).
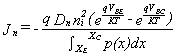(1.28 )
Per escriure aquesta expressió s’ha fet una aproximació i
es suposar que el coeficient de difusió Dn és constant. En realitat
varia amb la distància, però en general a la base és una funció que varia poc i
per aquesta raó s’agafa un valor promig constant.
A l’expressió donada a 1.28 apareix un terme de gran
importància i és la integral de la concentració de portadors majoritaris a la
base i a les zones de deplexió si aquest terme fos multiplicat per qAj ,
on q és la càrrega elèctrica i Aj és l’àrea.
Si es
multiplica l’equació 1.28 per Aj es té directament el corrent In
= Aj Jn. Aquest terme és el corrent total de portadors
minoritaris que són injectats a la base (electrons) des de les dues unions, és
a dir, és el corrent que és representat en el model d’ Ebbers-Moll de la figura 1.7 pel terme ICT (equació 1.29).
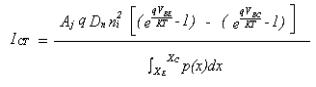
(1.29)
Si són comparades totes dues
expressions es té primer una diferència de signe, que ve de que In
es defineix que surt del col.letor, i ICT entra al col.lector. La
segona observació que es pot fer, i és la més important, és que IS
no és constant, tal com es pren en el model d'Ebers-Moll; és a dir, si agafem
l’expressió del corrent In i es comparada amb la del corrrent ICT
podem identificar que IS seria en aquest cas ( equació 1.30):
( 1.30 )
En
realitat, com es pot veure, els límits d’integració ara s’han definit com “xCO”
i “xEO”, i la concentració
de portadors majoritaris com p0 (x). Això és perquè:
a)
Els
límits d’integració en realitat depenen del nivell de polarització de les
unions BE i BC. Aleshores el que es fa es definir el paràmetre ISS (
que es correspon al paràmetre IS ) per les condicions en què la
tensió VBE i VBC són zero, i
b)
p0
(x) representa la concentració de forats en aquestes condicions d’equilibri a
la regió neutral i a la de base.
1.2.2.2.2
La
càrrega QB
Com s’ha indicat a l’expressió 1.29 ens apareix una integral que es pot identificar amb la càrrega de majoritaris a la base si aquest terme fos multiplicat per qAj. Aquesta càrrega es defineix com QB (equació 1.31 ).
( 1.31 )
Es defineix la càrrega QB0
per a les condicions d’equilibri, és a dir, la
tensió VBE i VBC són zero (equació 1.32).
( 1.32 )
Es
té així per a QB0 els límits d’integració
per a les condicions d’equilibri, i per a QB els seus límits depenen
de les condicions de polarització. Es defineix la càrrega normalitzada a la base qb
com (equació 1.33 ):
(
1.33 )
Si es té present aquesta darrera definició i l’equació 1.29, si es multiplica i divideix aquesta per QB0, s’arribarà a l’equació final (1.34)
(1.34)
En
el model d’ Ebbers-Moll es té IS i aquest és un paràmetre constant.
Ara es defineix una nova IS que és la constant ISS ( que
és el paràmetre IS del PSPICE) i que és la constant fonamental per a
les condicions de polarització zero, i qb. Aquesta dependència de la
nova IS amb la polarització portarà els efectes d’alta injecció i
modulació de la base. Cal però determinar la depèndència de qb amb
la polarització.
Aquesta càrrega de majoritaris té diferents componets com
són: a) la càrrega que es té quan no hi ha cap tensió aplicada QBo,
b) les càrregues emmagatzemades a les unions d'emissor i de col.lector, i c)
els corrents d'injecció de portadors minoritaris a la base. Quan s’està lluny
de les condicions d’alta injecció, aquesta variació de càrrega de portadors
majoritaris a la base és menyspreable, però quan s’està en forta injecció,
aleshores, sí que es té una variació important de la concentració dels
portadors majoritaris, degut a la injecció dels minoritaris a la base, sigui
per la unió BE o BC.
Es pot escriure qb en funció d’aquestes diferents
components (equació 1.35)
|
|
on els diferents termes es defineixen (
equacions 1.36 i 1.37 ):
( 1.36 )
i a on
|
|
Es pot ara definir que (equació 1.38 )
( 1.38 )
on s´han agrupat els termes com s’indica a les
equacions 1.39:
(1.39)
Aleshores es pot aïllar qb en termes de q1 i q2 ( equació 1.40 ).
( 1.40 )
Les expressions de q1 i q2 es donen a les equacions 1.41.
(1.41)
El
terme q1 és el que té cura dels efectes de modulació del canal. Quan
no es té cap polarització, q1=1, però si es té per exemple totes dues unions en
inversa, q1<1. Això indicarà que l'amplada elèctrica de la base es fa més
petita que la física.
El
terme q2 és el que té cura dels efectes d'alta injecció. Així doncs,
quan s’està en condicions de baixa injecció q2<< q12
i qb és pràcticament q1. Quan s’està en règim d'alta
injecció, es té que q2>> q12 i qb
és aproximadament arrel de q2.
Així doncs en condicions d’alta injecció, qb = sqrt (q2), i si es fixa VBC = 0, qb té el valor (equació 1.42).
( 1.42 )
Com IC = ICT es demostra el fet del canvi del pendent en el cas d’ alta injecció (equació 1.43 ).
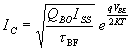( 1.43 )
L’intersecció entre el corrent de col.lector per corrents mitjos i el corrent de col.lector per a les condicions d’alta injecció defineixen el corrent de colze I KF. D’una forma anàloga es defineix el paràmetre I KR, que és el corrent de colze quan el transistor treballa en mode actiu invers.
D’ aquesta forma s’han inclós els paràmetres : IKF i I KR .
Els termes associats a la modulació de l’amplada de la base són els paràmetres VAF i VAR, per al mode actiu directe e invers respectivament.
1.3 Altres paràmetres: les resistències.
Per tal de millorar la modelització del transistor bipolar s’inclouen tres constants que fan referència a les resistències òhmiques que hi ha entre els terminals i les regions actives de l’emissor, base i col.lector. A la figura 1.11 és representen aquestes resistències.
Figura 1.10: resistències.
1.3.1
La resistència de col.lecor rC
L’efecte de la resistència de col.lector es tradueix en una caiguda del nivell de corrent de col.lector en la regió de saturació. Aquesta és la regió en què la tensió VCE és baixa.
1.3.2
La resistència d’emissor rE
Per aconseguir un transistor amb un guany b gran és necessari que l’eficiència d’injecció g sigui un valor el més proper a la unitat. Per aquesta raó, a nivell de la realizació del transistor, l’emissor està molt dopat; d’aquesta forma el nivell d’injecció d’electrons (recordem que ens referim al transistor N+PN) serà gran i predominant. És per aquesta raó que la resistència associada a l’emissor és molt petita i la resistència rE és pràcticament la resistència de contacte. En general és un valor que es pren com menyspreable. El seu efecte principal és dóna per la reducció de la tensió VBE que veu la unió en un factor rEIE. Fa doncs que disminueixi el corrent de base, i en conseqüència el corrent de col.lector. Aquest terme pot portar a un error important en la determinació de la resistència de base.
1.3.3 La resistència de base rB
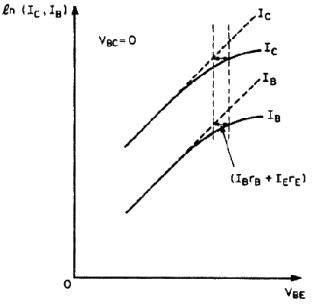
La resistència de
base, rB, és molt important sobre les respostes transitòries i sobre
la petita senyal. També existeix una dificultat important amb la seva mesura
experimental per la seva dependència del punt d'operació. SPICE, però, la
considera constant. Si es considera que el transistor treballa en mode actiu
directe, i amb VBC=0, la
gràfica del ln IB vs VBE resultant és la que és mostra a la figura 1.12. Com
pot observar-se el comportament és semblant al que es troba en el cas del diode
quan s’estudia l’efecte de la resistència òhmica RS.
Figura 1.12: Els efectes de les
resistències rB i rE.
1.4 Els
efectes capacitius: les capacitats de junció.
Respecte a les capacitats de junció ens podem referir a la teoria de la capacitat de junció d'una unió PN. El transistor no és més que dos diodes enfrontats de forma que la caracterització de cada capacitat es podrà fer per separat curt-circuitant l'altre. Els paràmetres associats són els mateixos que ja coneixem però definits per cada junció. Així doncs els paràmetres són: a) CJE, VJE i MJE per a la unió base-emissor, i b) CJC, VJC i MJC per a la unió base-col.lector. (Com a recordatori: CJ representa la capacitat de junció a polarització zero, VJ la tensió de la unió i el coeficient de junció MJ.
1.5
Els efectes amb la temperatura
Els efectes de la temperatura són considerats modificant els valors d'alguns dels paràmetres del model inicial. S'ha de recordar que es considera que els paràmetres han estat mesurats a temperatura de 27 ºC. Els paràmetres que són modificats són: Is, ISE, ISC, VJE, VJC, bF, bR, CJC, CJE i el coeficient FC de la capacitat de difusió. En aquesta pràctica ens centrarem en extreure el paràmtere associat a la variació del guany en termes de la temperatura XTB. Tant per al guany en directe com en inversa la BETA(T) és del tipus:
(1.44)
1.6
El model PSPICE: paràmetres estudiats
El model implementat al PSPICE és el de Gummel-Poon, i s’ha vist que modelitza els següents efectes:
- Transistor ideal: en base al model d’Ebbers-Moll modelitza els guanys en directe, inversa i les capacitats.
-
Els corrents
de base per baixos nivells d’injecció, en mode actiu directe i invers.
- Els efectes d’alta injecció.
- Els efectes de la modulació de l’amplada de la base.
-
Els efectes
de les resistències òhmiques.
-
Els efectes
tèrmics.
Aquest
model , però, no considera per exemple les tensions de ruptura de les unions.
En el present capítol s’han tractat els principals paràmetres en DC i
capacitius. No s’han tractat els paràmetres associats als efectes transitoris.
2.
Extracció dels paràmetres.
En el següent
apartat es tractarà la metodologia que es segueix per extreure els paràmetres que han estat presentats en l’apartat 1.
Tota aquesta metodologia és una de possible. Dins de la literatura poden
presentar-se altres metologies que no són ni millors ni pitjors, són
sencillament diferents.
2.1 Extracció dels paràmetres per a corrents mitjos, baixos nivells d’injecció i alts.
Es suposa que es té el transistor
treballant en mode actiu directe, amb la condició de VBC=0, és a
dir, amb base i col.lector curtcircuitats. Si es representen els logaritmes
dels corrents de col.lector i de base es té una situació com la de la figura
2.1.
Figura 2.1: Paràmetres IS, ISE,
nE, nf, bF i I KF.
Com
pot observar-se es pot fer l'extracció dels següents paràmetres, estudiant les
diferents regions de baixos, alts i mitgos currents, pel transistor treballant
en mode actiu directe.
2.1.1 Els paràmetres per corrents mitjos i baixos.
De l’expressió del
corrent de base, com del corrent de col.lector, en el rang de corrents mitjos
els termes predominants són els termes exponencials amb els coeficients nF
i nE . D’aquesta forma si es representa el logaritme d’aquets termes
pot trobar-se directament dels pendents de les rectes i dels seus talls amb
l’eix del logaritme del corrent els paràmetres IS i IS / bF . D’aquesta forma es troben
els paràmetre ISS del model de Gummel-Poon, i el guany en directe,
després. Els coeficients nF es troba dels pendents, siqui del corrent
de col.lector, o del corrent de base.
Per trobar els paràmetres ISE,
nE, s’han de fixar amb el corrent de base per baixos nivells de
conducció. Tal com s’ha indicat anteriorment, el terme predominant és aleshores
pel corrent de base
|
|
Si
es representa la derivada del logaritme del corrent de base, i es trobar el
pendent màxim a la zona de corrents baixes es podrà determinar nE . Fent servir aquests punt i el
valor del pendent màxim s’escriu l'equació de la recta i d’aquesta trobar ISE.
Quan el
transistor és polaritzat en mode actiu invers, fixant la condició de VBE
= 0, la metodologia per a l’extracció dels paràmetres ara associats és la
mateixa, però ara s’haurà d’agafar el corrent d’emissor pel de col.lector. A la
figura 2.2 es representen els corrents i paràmetres.
Figura 2.2: Paràmetres ISC, nR,
nC bR i I
KR.
Per a l’extracció dels paràmetres de colze es fa referència a l’equació 1.43 per al transistor treballant en mode actiu directe. El corrent de colze que determina el canvi de corrents mitjos a alts nivells d’ injecció es caracteritza pel fet que el pendent associat a la recta es fa meitat respecte al de la recta que defineix el comportament per als corrents mitjos; és a dir, en la representació dels logaritmes dels corrent, la regió on es té el nivell d’alta injecció és una recta de pendent meitat.
2.1.2 Els guanys en directe i en
inversa
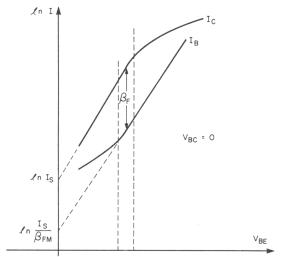
Per a l'extracció dels
paràmetres BF i BR es podran fer servir diferents mètodes: a) mitjançant el
tall amb amb l'eix del logaritme dels corrents (figura 2.2) de la recta del
corrent de base per corrents mitjos; b) mitjançant la representació de l guany
del transistor en termes del corrent de col.lector, i c) de la diferència entre
corrent de col.lector i corrent de base (figura 2.3), en el cas de trobar el guany
en modus actiu directe (forward).
Figura 2.3: Extracció de la BETA.
2.1.3 Extracció dels paràmetres de
les tensions d' Early
A la regió lineal o zona de
corrents mitjos, el corrent de col.lector pot aproximar-se a
|
|
en aquesta regió es té que qb
és aproximadament q1. Aleshores si es considera una tensió de base
fixa, el corrent de col.lector serà proporcional a 1 -VBC/VA
-VBE/VB. Si VCE és bastant més gran que VBE,
aleshores serà proporcional a 1 +VCE/VA. Extrapolant IC
amb el seu tall amb el eix "x" es trobarà el paràmetre VA.
2.1.4 Extracció dels paràmetres
tèrmics
Els paràmetres tèrmics són XTI i XTB. El primer va ésser
estudiat quan va tractar-se la pràctica dedicada al diode (capítol 1), i és per
aquesta raó que no tornarà a ésser estudiat ara. El paràmetre nou és el XTB.
Per a la seva extracció s'haurà de fer referència a l'equació (1.44). Com
s'haurà de trobar el paràmetre BETA per a dues temperatures diferents s'haurà
d' escollir entre els possibles mètodes d'extracció del guany que sigui més bo.
2.1.5 Extracció de les resistències
Les resistències són incloses en el
model de la forma representada a la figura 1.10. La resistència d' emissor és
modelitzada com un valor constant. Aquesta representa la resistència entre la
zona activa i el terminal. Per mesurar-la heu de ficar el vostre transistor en
un règim de forta saturació. Per això
per exemple fiquem IC=0, i fer una escombrada en corrent a la base.
La tensió VC'E' = VCE,SAT+ RE*IB.
Representant la tensió vs. IB podem treure RE.
La resistència de base, rB,
és molt important sobre les respostes transitòries i sobre la petita senyal.
També existeix una dificultat important amb la seva mesura experimental per la
seva dependència del punt d'operació. SPICE, però, la considera constant i dóna
una gràfica del ln IB vs VBE, amb VBC=0,
semblant a la del cas del diode. Coneixent el valor de RE, podem per
diferents valors de DV=RBIB+REIE
i mitjantçant una regressió trobar RB.
Per trobar la resistència de col.letor rC, suposarem que el transistor esta treballant a la zona de saturació. De la inversa del pendent del current de col.lector vs tensió VCE trobaríem la resistència.
2.1.6 Extracció dels paràmetres
capacitius
Finalment
tractarem l'extracció dels paràmetres associats a las capacitats d'unió
resultants de les càrregues fixes a les zones de càrrega espaials. Com ja s'ha
vist en el cas del diode la capacitat de junció (no confondre amb la de
difusió), es pot escriure com
|
|
On CJo representa la
capacitat de junció a tensió zero, m és el coeficient de MJ, i f representa el potencial de
construcció de la unió. Nosaltres tindrem les capacitats associades a les
unions emissor-base i base-col.lector.
Si representeu en escala logarítmica les quantitasts C (la capacitat) en funció
de la tensió, tindrem una recta. Per nivells de tensió elevats podreu trobar el
pendent m. Per al cas de la junció BE és el paràmetre MJE i per la junció BC és
MJC.
Trobats els valors de CJE(0) i
CJC(0), amb els valors de MJE i MJC podrem trobar per qualsevol punt
el valor de VJE i VJC.
Annex: Realització
experimental
Donat el següent model:
.model Qtransistor NPN(IS=.1F BF=500 BR=2
NF=1 NR=1 ISE=100F ISC=100F NE=3 NC=3
+IKF=100U IKR=.1U VAF=60 VAR=30 RC=10 RE=.1 RB=6 CJE=2P VJE=0.75 MJE=0.33
+CJC=0.1P VJC=0.75 MJC=0.33 TF=100P
TR=50P XTB=0.5)
s'hauran d'estudiar:
a)
Tots els
paràmetres en directe (modus actiu directe): IS, ISE, NF, NE, IKF, VAF
b)
Tots els
paràmetres en modus actiu invers: ISC,
NR, NC, IKR, VAR
c)
Determinar
els paràmetres BF i BR pels diferents mètodes
d)
Trobar el
paràmetre tèrmic XTB.
e)
Determinar
els paràmetres capacitius per totes dues juncions.
f)
Per quina
raó per determinar els corrents de colze s'ha de fer servir el punt on el
pendent
és meïtat?
Resum dels paràmetres que s'han estudiat:
|
Nom |
Area |
Paràmetre |
Unitats |
|
IS rC rE rB ISE ISC NE NC NR NS CJE VJE MJE CJC VJC MJC IKF IKR VAF VAR BF BR EG XTI XTB |
* * * * * * * * |
Corrent de saturació Resistència de col.lector Resistència d' emissor Resistència de base Corrent de fuites
BE Corrent de fuites
BC Coeficient d’idealitat Base-Emissor Coeficient d’idealitat Base-Col.lector Coeficient d’idealitat Base-Emissor Inversa Coeficient d’idealitat Base-Col.lector Inversa Capacitat de junció a tensió zero BE Potencial d’unió BE Coeficient gradent d’unió BE Capacitat de junció a tensió zero BC Potencial d’unió BC Coeficient gradent d’unió BC Corrent de colze en modus actiu directe Corrent de colze en
modus actiu invers Tensió d' Early en directe Tensió d' Early en inversa Guany en modus actiu directe màxim ideal Guany en modus
actiu invers màxim ideal Energia GAP Variació amb la temperatura de Is Coeficient variació BF i BR amb la temperatura |
Amps Ohms Ohms Ohms Amps Amps Farads Volts Farads Volts Amps Amps Volts Volts Elecn-Volts |